Suprafața unui cilindru – Explicații și exemple
Înainte de a trece la subiectul suprafeței unui cilindru, să trecem în revistă un cilindru. În geometrie, un cilindru este o figură tridimensională cu două baze circulare paralele între ele și o suprafață curbă.
Cum se găsește suprafața unui cilindru?
Suprafața unui cilindru este suma a două fețe circulare paralele și congruente și a suprafeței curbe.
Acest articol va discuta despre cum se găsește suprafața totală și suprafața laterală a unui cilindru.
Pentru a calcula suprafața unui cilindru, trebuie să găsiți aria bazei (B) și aria suprafeței curbe (CSA). Prin urmare, aria suprafeței sau suprafața totală a unui cilindru este egală cu suma dintre aria bazei înmulțită cu doi și aria suprafeței curbe.
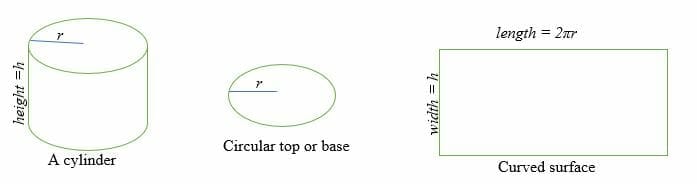
Suprafața curbă a unui cilindru este egală cu un dreptunghi a cărui lungime este 2πr și a cărui lățime este h.
Unde r = raza feței circulare și h = înălțimea cilindrului.
Aria suprafeței curbe = Aria unui dreptunghi =l x w = πdh
Aria bazei, B = Aria unui cerc = πr2
Formula ariei unui cilindru
Formula pentru aria totală a suprafeței unui cilindru este dată de formula:
:
Aria suprafeței totale a unui cilindru = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Unde 2πr2 este aria fețelor circulare superioară și inferioară, iar 2πrh este aria suprafeței curbe.
Prin luarea lui 2πr ca factor comun din RHS, obținem;
TSA = 2πr (h + r) ……………………………………. ……………………………………. (Formula suprafeței unui cilindru)
Să rezolvăm exemple de probleme care implică suprafața unui cilindru.
Exemplul 1
Găsește suprafața totală a unui cilindru a cărui rază este de 5 cm și înălțime de 7 cm.
Soluție
Potrivit formulei,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Exemplul 2
Găsește raza unui cilindru a cărui suprafață totală este de 2136,56 picioare pătrate, iar înălțimea este de 3 picioare.
Soluția
Dat fiind:
TSA = 2136.56 picioare pătrate
Înălțime, h = 3 picioare
Dar, TSA = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
Prin proprietatea distributivă a înmulțirii pe RHS, avem,
2136.56 = 18.84r + 6.28r2
Divizați fiecare termen cu 6.28
340.22 = 3r + r2
r2 + 3r – 340.22 = 0 ……… (o ecuație pătratică)
Rezolvând ecuația cu ajutorul formulei pătratice, obținem,
r = 17
Din acest motiv, raza cilindrului este de 17 picioare.
Exemplul 3
Costul de vopsire a unui recipient cilindric este de 0,04 dolari pe cm2. Găsiți costul vopsirii a 20 de recipiente cu raza de 50 cm și înălțimea de 80 cm.
Soluție
Calculați suprafața totală a celor 20 de recipiente.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
Suprafața totală a 20 de containere = 40.820 cm2 x 20
=816.400 cm2
Costul vopsitului = 816.400 cm2 x 0 $.04 per cm2
= 32.656 $.
Deci, costul vopsitului a 20 de containere este de 32.656 $.
Exemplul 4
Căutați înălțimea unui cilindru dacă suprafața totală a acestuia este de 2552 in2 și raza este de 14 in.
Soluție
Dat fiind:
TSA = 2552 in2
Radiu, r = 14 in.
Dar, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Divizați ambele părți cu 87,92 pentru a obține,
29.026 = 14 + h
Subtirați cu 14 pe ambele părți.
h = 15
În consecință, înălțimea cilindrului este de 15 in.
Aria suprafeței laterale a unui cilindru
După cum s-a spus mai devreme, aria suprafeței curbe a unui cilindru este ceea ce se numește aria suprafeței laterale. Cu cuvinte simple, aria suprafeței laterale a unui cilindru este aria suprafeței unui cilindru, excluzând aria bazei și a fundului (suprafața circulară).
Formula dă aria suprafeței laterale a unui cilindru;
LSA = 2πrh
Exemplul 5
Căutați aria suprafeței laterale a unui cilindru al cărui diametru este de 56 cm și înălțimea de 20 cm.
Soluție
Dat fiind:
Diametrul = 56 cm, deci raza, r =56/2 = 28 cm
Înălțimea, h = 20 cm
Prin, formula,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Așa, suprafața laterală a cilindrului este de 3516,8 cm2.
Exemplul 6
Suprafața laterală a unui cilindru este de 144 ft2. Dacă raza cilindrului este 7 ft, găsiți înălțimea cilindrului.
Soluție
Dat;
LSA = 144 ft2
Rază, r = 7 ft
.




