Scheefheid – Snelle inleiding, voorbeelden & formules

Scheefheid – Snelle inleiding, voorbeelden & formules

Scheefheid is een getal dat aangeeft in welke mate
een variabele asymmetrisch verdeeld is.

• Positieve (Rechter) Scheefheid Voorbeeld
• Negatieve (Linker) Scheefheid Voorbeeld
• Volkingsscheefheid – Formule en Berekening
• Volkingsscheefheid – Formule en Berekening
• Volkingsscheefheid – Voorbeeld
• Volkingsscheefheid –
• Volkingsscheefheid –

. Formule en berekening

• Skewness in SPSS
• Skewness – Implications for Data Analysis

Positive (Right) Skewness Voorbeeld

Een wetenschapper laat 1,000 mensen een aantal psychologische tests laten afleggen. Voor test 5 hebben de testscores scheefheid = 2,0. Een histogram van deze scores is hieronder weergegeven.

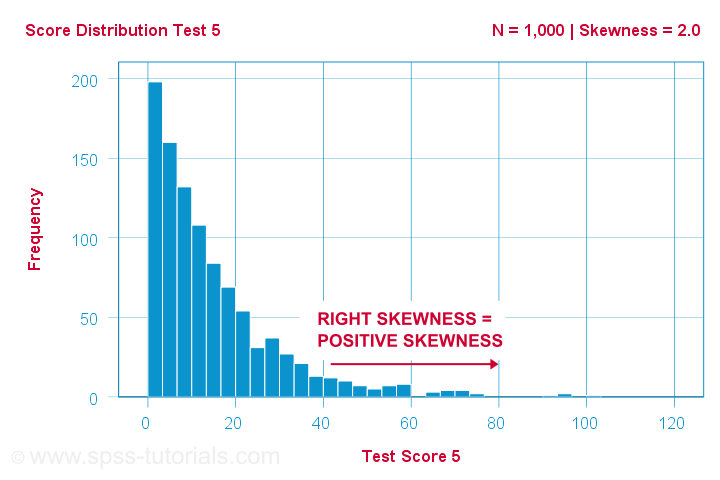
Het histogram vertoont een zeer asymmetrische frequentieverdeling. De meeste mensen scoren 20 punten of lager, maar de rechterstaart strekt zich uit tot 90 of zo. Deze verdeling is rechts scheef.
Als we langs de x-as naar rechts gaan, gaan we van 0 naar 20 naar 40 punten en zo verder. Dus naar rechts in de grafiek worden de scores positiever. Scheefheid naar rechts is dus positieve scheefheid, dat wil zeggen scheefheid > 0. Dit eerste voorbeeld heeft scheefheid = 2,0 zoals aangegeven in de rechterbovenhoek van de grafiek. De scores zijn sterk positief scheef.

Negatieve (Linker) Scheefheid Voorbeeld

Een andere variabele -de scores op test 2- blijken scheefheid = -1.0 te hebben. Hun histogram is hieronder weergegeven.

Het grootste deel van de scores ligt tussen 60 en 100 of zo. De linkerstaart is echter wat uitgerekt. Deze verdeling is dus links scheef.
Rechts: naar links, naar links. Als we de x-as naar links volgen, gaan we naar negatievere scores. Daarom is linkse scheefheid negatieve scheefheid. En inderdaad, scheefheid = -1,0 voor deze scores. Hun verdeling is links scheef. Ze is echter minder scheef – of symmetrischer – dan ons eerste voorbeeld dat scheefheid = 2.0 had.

Symmetrische verdeling impliceert nul scheefheid

Ten slotte hebben symmetrische verdelingen scheefheid = 0. De scores op test 3 – met scheefheid = 0.1 – komen in de buurt.

Nu, waargenomen verdelingen zijn zelden precies symmetrisch. Dit wordt vooral gezien bij sommige theoretische steekproefverdelingen. Enkele voorbeelden zijn

• de (standaard) normale verdeling;
• de t-verdeling en
• de binomiale verdeling als p = 0,5.

Deze verdelingen zijn allemaal exact symmetrisch en hebben dus scheefheid = 0.000…

Volkingsscheefheid – Formule en berekening

Als u scheefheden voor een of meer variabelen wilt berekenen, laat u de berekeningen gewoon over aan wat software. Maar -voor de volledigheid- zal ik toch de formules vermelden.
Als uw gegevens uw gehele populatie bevatten, berekent u de scheefheid van de populatie als:
$$Populatie-skewness = \Sigma}{X_i – \mu}{\sigma}{N}$$
waar

• (X_i) elke individuele score is;
• (φ) is het populatiegemiddelde;
• (φ) is de standaardafwijking van de populatie en
• (N) is de populatiegrootte.

Voor een voorbeeldberekening met deze formule, zie dit Googlesheet (hieronder weergegeven).

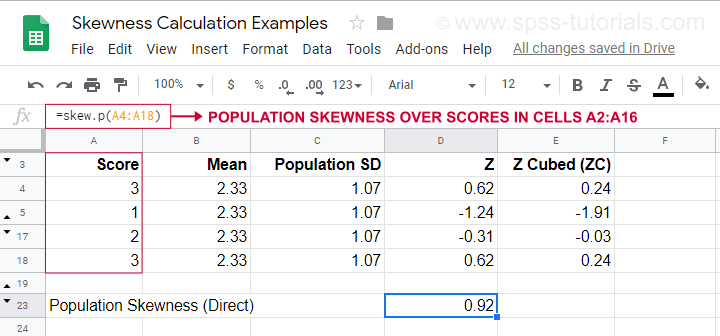
Hier wordt ook getoond hoe de scheefheid van de populatie rechtstreeks kan worden verkregen met behulp van=SKEW.P(…)waarbij “.P” “populatie” betekent. Dit bevestigt de uitkomst van onze handmatige berekening. Helaas berekenen noch SPSS noch JASP de scheefheid van de populatie: beide zijn beperkt tot de scheefheid van de steekproef.

Skewness van een steekproef – Formule en berekening

Als uw gegevens een eenvoudige aselecte steekproef uit een of andere populatie zijn, gebruikt u
$$SampleScheefheid = \frac{NNBCDotSigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$
waar

• (X_i) elke individuele score is;
• (\overline{X}) het steekproefgemiddelde is;
• (S) de steekproef-standaard-afwijking en
• (N) de steekproefgrootte is.

Een rekenvoorbeeld staat in dit Googlesheet (hieronder).

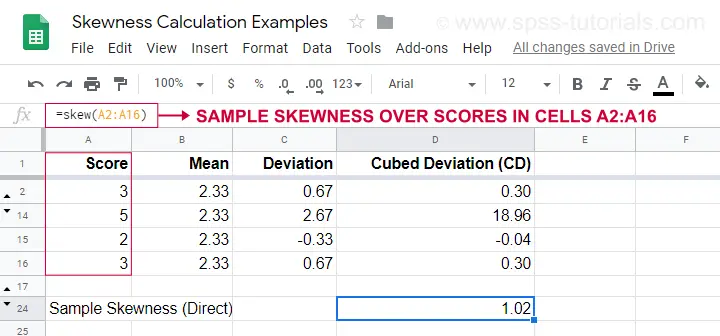
Een eenvoudiger optie om de scheefheid van de steekproef te verkrijgen is met=SKEW(…).die de uitkomst van onze handmatige berekening bevestigt.

Skewness in SPSS

In de eerste plaats verwijst “skewness” in SPSS altijd naar sample skewness: het gaat er rustig van uit dat uw gegevens een steekproef zijn en niet een hele populatie. Er zijn genoeg opties om het te verkrijgen. Mijn favoriet is via MEANS omdat de syntaxis en de uitvoer schoon en eenvoudig zijn. De onderstaande schermafdrukken helpen u op weg.

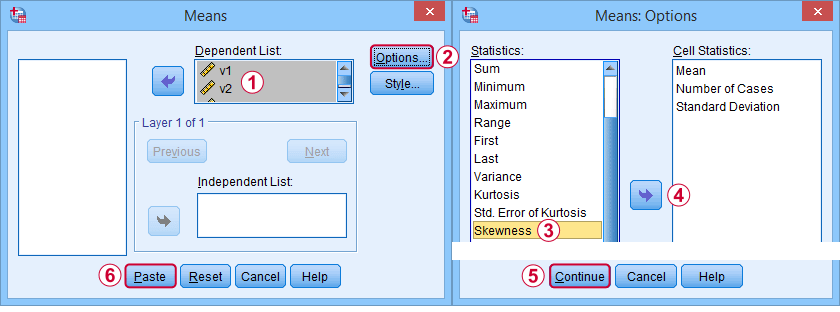
De syntaxis kan zo simpel zijn alsmeans v1 to v5
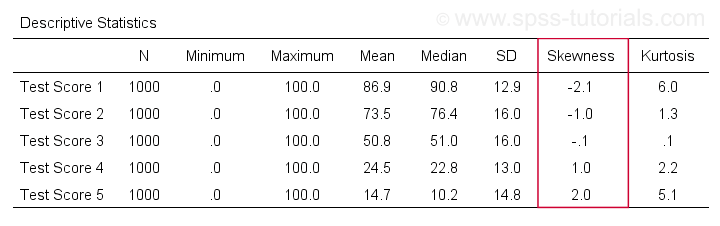
/cells skew.Een zeer complete tabel -inclusief gemiddelden, standaardafwijkingen, medianen en meer- wordt uitgevoerd metmeans v1 to v5
/cells count min max mean median stddev skew kurt.Het resultaat staat hieronder.

Skewness – Implications for Data Analysis

Veel analyses -ANOVA, t-tests, regressie en andere- vereisen de normaliteitsveronderstelling: variabelen moeten normaal verdeeld zijn in de populatie. De normale verdeling heeft scheefheid = 0. Het waarnemen van aanzienlijke scheefheid in sommige steekproefgegevens suggereert dus dat de normaliteitsaanname geschonden is.
Zulke schendingen van normaliteit zijn geen probleem voor grote steekproefgroottes -zeg N > 20 of 25 of zo. In dat geval zijn de meeste tests bestand tegen dergelijke schendingen. Dit is het gevolg van het centrale limiettheorema. Kortom, voor grote steekproefgroottes is scheefheid geen echt probleem voor statistische tests. Scheefheid gaat echter vaak gepaard met grote standaardafwijkingen. Dit kan resulteren in grote standaardfouten en een lage statistische power. Zo kan een aanzienlijke scheefheid de kans verkleinen om een of andere nulhypothese te verwerpen en zo een of ander effect aan te tonen. In dat geval kan een niet-parametrische test een verstandiger keuze zijn omdat die meer power heeft. Schendingen van de normaliteit vormen een reële bedreiging voor kleine steekproeven van -zeg- N < 20 of zo. Bij kleine steekproefgroottes zijn veel toetsen niet bestand tegen een schending van de normaliteitsveronderstelling. De oplossing is -nogmaals- het gebruik van een niet-parametrische test omdat deze geen normaliteit vereisen.
Last but not least, er is geen statistische test om te onderzoeken of de scheefheid van de populatie = 0. Een indirecte manier om dit te testen is een normaliteitstest zoals

• de Kolmogorov-Smirnov normaliteitstest en
• de Shapiro-Wilk normaliteitstest.

Wanneer normaliteit echter echt nodig is – bij kleine steekproefgroottes – hebben dergelijke toetsen een laag vermogen: het is mogelijk dat zij geen statistische significantie bereiken, zelfs wanneer de afwijkingen van de normaliteit ernstig zijn. Zo geven ze u vooral een vals gevoel van veiligheid.