Beginning Algebra
Learning Objectives
- Plot geordende paren
- Identify the components of the coordinate plane
- Geordende paren tekenen op het coördinatenvlak
- Kwadranten bepalen op het coördinatenvlak
- De vier kwadranten van een coördinatenvlak bepalen
- Gegeven aan een geordend paar, bepaal het kwadrant
Het coördinatenvlak werd eeuwen geleden ontwikkeld (in 1637 om precies te zijn) en verfijnd door de Franse wiskundige René Descartes. Ter ere van hem wordt het systeem soms het cartesiaanse coördinatenstelsel genoemd. Het coördinatenvlak kan worden gebruikt om punten uit te zetten en lijnen te tekenen. Dit systeem stelt ons in staat om algebraïsche relaties visueel te beschrijven, en helpt ons ook om algebraïsche concepten te creëren en te interpreteren.
De componenten van het coördinatenvlak
Je hebt waarschijnlijk al eens een coördinatenvlak gebruikt. Heb je bijvoorbeeld ooit een gerasterde overlay gebruikt om de positie van een object in kaart te brengen? (Dit wordt ook vaak gedaan met wegenkaarten.)

Deze “kaart” gebruikt een horizontaal en verticaal raster om informatie over de plaats van een voorwerp over te brengen. Merk op dat de letters A-F bovenaan staan, en de nummers 1-6 langs de linkerrand. De algemene plaats van een voorwerp op deze kaart kan worden gevonden door de letter en het nummer van het rastervak te gebruiken. Bijvoorbeeld, u kunt het item vinden op vak “4F” door uw vinger horizontaal te bewegen naar de letter F en dan recht naar beneden zodat u in lijn bent met de 4. U zult een blauwe schijf vinden op deze plaats op de kaart.
Het coördinatenvlak heeft soortgelijke elementen als het hierboven getoonde rooster. Het bestaat uit een horizontale as en een verticale as, getallenlijnen die elkaar in rechte hoeken snijden. (Ze staan loodrecht op elkaar.)
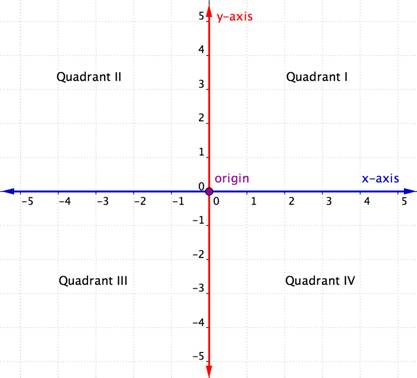
De horizontale as in het coördinatenvlak wordt de x-as genoemd. De verticale as wordt de y-as genoemd. Het punt waar de twee assen elkaar snijden, wordt de oorsprong genoemd. De oorsprong ligt op 0 op de x-as en 0 op de y-as.
Locaties op het coördinatenvlak worden beschreven als geordende paren. Een geordend paar vertelt u de locatie van een punt door het relateren van de locatie van het punt langs de x-as (de eerste waarde van het geordende paar) en langs de y-as (de tweede waarde van het geordende paar).
In een geordend paar, zoals (x, y), de eerste waarde wordt de x-coördinaat en de tweede waarde is de y-coördinaat. Merk op dat de x-coördinaat vóór de y-coördinaat staat. Aangezien de oorsprong een x-coördinaat van 0 en een y-coördinaat van 0 heeft, wordt het geordende paar geschreven als (0, 0).
Bekijk het onderstaande punt.

Om de plaats van dit punt te bepalen, begint u bij de oorsprong (0, 0) en beweegt u rechts langs de x-as totdat u zich onder het punt bevindt. Kijk naar het label op de x-as. De 4 geeft aan dat je, vanaf de oorsprong, vier eenheden naar rechts bent gereisd langs de x-as. Dit is de x-coördinaat, het eerste getal in het geordende paar.
Vanaf 4 op de x-as ga je omhoog naar het punt en let op het getal waarmee het op één lijn ligt op de y-as. De 3 geeft aan dat je, na het verlaten van de x-as, 3 eenheden omhoog bent gereisd in de verticale richting, de richting van de y-as. Dit getal is de y-coördinaat, het tweede getal in het geordende paar. Met een x-coördinaat van 4 en een y-coördinaat van 3 heb je het geordende paar (4, 3).
Laten we eens kijken naar een ander voorbeeld.
Voorbeeld
Beschrijf het afgebeelde punt als een geordend paar.

Beschrijf het punt dat is weergegeven als een geordend paar
Punten uitzetten in het coördinatenvlak
Nu u weet hoe u de x- en y-assen moet gebruiken, kunt u ook een geordend paar uitzetten. Onthoud dat beide processen beginnen bij de oorsprong – het begin! Het volgende voorbeeld laat zien hoe u een grafiek kunt maken van het geordende paar (1,3).
Voorbeeld
Platteer het punt (1, 3).
In het vorige voorbeeld waren zowel de x- als de y-coördinaten positief. Wanneer een (of beide) coördinaten van een geordend paar negatief is, moet u in de negatieve richting langs een of beide assen bewegen. Beschouw het onderstaande voorbeeld waarin beide coördinaten negatief zijn.
Voorbeeld
Plaat het punt (-4,-2).

De x-coördinaat is -4 omdat deze als eerste in het geordende paar voorkomt. Begin bij de oorsprong en beweeg 4 eenheden in negatieve richting (naar links) langs de x-as.
De y-coördinaat is -2 omdat hij de tweede is in het geordende paar. Beweeg nu 2 eenheden in negatieve richting (naar beneden). Als je nu naar de y-as kijkt, moet je op één lijn staan met -2 op die as.
De stappen voor het uitzetten van een punt zijn hieronder samengevat.
Stappen voor het uitzetten van een geordend paar (x, y) in het coördinatenvlak
- Bepaal de x-coordinaat. Begin bij de oorsprong en beweeg horizontaal, in de richting van de x-as, de afstand gegeven door de x-coördinaat. Als de x-coördinaat positief is, beweegt u naar rechts; als de x-coördinaat negatief is, beweegt u naar links.
- Bepaal de y-coördinaat. Begin bij de x-coördinaat en beweeg verticaal, in de richting van de y-as, de afstand gegeven door de y-coördinaat. Als de y-coördinaat positief is, beweegt u omhoog; als de y-coördinaat negatief is, beweegt u omlaag.
- Teken een punt op de eindlocatie. Label het punt met het geordende paar.
Punten uitzetten op het coördinatenvlak
Kwadranten identificeren en gebruiken om punten uit te zetten
Het coördinatenvlak wordt door de snijpunten van x- en y-as in vier secties verdeeld. Deze vier doorsneden worden kwadranten genoemd. Kwadranten worden benoemd met de Romeinse cijfers I, II, III en IV, te beginnen met het kwadrant rechtsboven en verder tegen de klok in.
Gerangschikte paren binnen een bepaald kwadrant hebben bepaalde kenmerken gemeen. Kijk naar elk kwadrant in de grafiek hieronder. Wat valt u op aan de tekens van de x- en y-coördinaten van de punten binnen elk kwadrant?
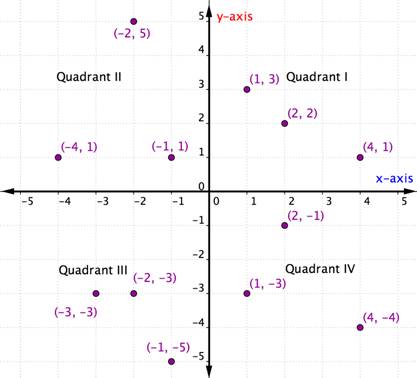
Binnen elk kwadrant zijn de tekens van de x- en y-coördinaten van elk geordend paar hetzelfde. Zij volgen ook een patroon, dat in de tabel hieronder wordt geschetst.
| Kwadrant | Algemene vorm van punt in dit kwadrant | Voorbeeld | Beschrijving |
|---|---|---|---|
| I | (+,+) | (5,4) | Gaande van de oorsprong, ga langs de x-as in positieve richting (rechts) en langs de y-as in positieve richting (omhoog). |
| II | (-,+) | (-5,4) | Vanaf de oorsprong langs de x-as in negatieve richting (naar links) en langs de y-as in positieve richting (naar boven) gaan. |
| III | (-,-) | (-5,-4) | Gaande van de oorsprong, ga langs de x-as in negatieve richting (links) en langs de y-as in negatieve richting (omlaag). |
| IV | (+,-) | (5,-4) | Gaande van de oorsprong, langs de x-as in positieve richting (naar rechts) en langs de y-as in negatieve richting (naar beneden). |
Als je eenmaal de kwadranten in het assenvlak kent, kun je het kwadrant van een geordend paar bepalen zonder er zelfs maar een grafiek van te maken door naar de bovenstaande grafiek te kijken. Hier is een andere manier om er over na te denken.
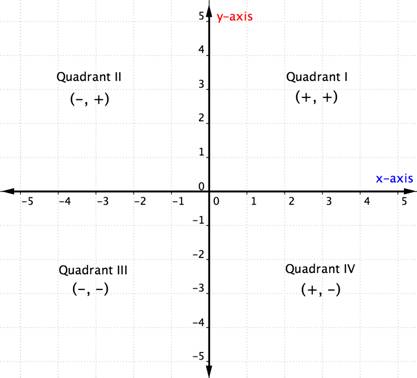
Het onderstaande voorbeeld laat zien hoe je de kwadrantligging van een punt kunt bepalen door alleen maar aan de tekens van zijn coördinaten te denken. Nadenken over de kwadrantligging alvorens een punt te plotten kan u helpen een fout te voorkomen. Het is ook nuttige kennis om te controleren of u een punt juist geplot hebt.
Voorbeeld
In welk kwadrant ligt het punt (-7,10)?
Voorbeeld
In welk kwadrant ligt het punt (-10,-5)?
Wat gebeurt er als een geordend paar een x- of y-coördinaat van nul heeft? Het voorbeeld hieronder toont de grafiek van het geordende paar (0,4).
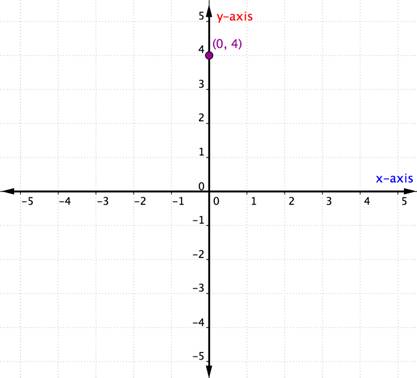
Een punt dat op een van de assen ligt, wordt niet beschouwd als liggend in een kwadrant. Het ligt gewoon op een van de assen. Wanneer de x-coördinaat 0 is, ligt het punt op de y-as. Op dezelfde manier ligt elk punt met een y-coördinaat van 0 op de x-as.
Kwadranten identificeren en gebruiken om punten uit te zetten
Samenvatting
Het assenvlak is een systeem om punten en lijnen in kaart te brengen en te beschrijven. Het coördinatenvlak bestaat uit een horizontale (x-)as en een verticale (y-)as. Het snijpunt van deze lijnen is de oorsprong, dat is het punt (0,0). Het coördinatenvlak is verdeeld in vier kwadranten. Samen maken deze kenmerken van het coördinatenstelsel de grafische voorstelling en communicatie over punten, lijnen en andere algebraïsche concepten mogelijk.





