Šikmost – rychlý úvod, příklady a vzorce
Šikmost je číslo, které udává, do jaké míry je
proměnná rozložena asymetricky.
- Příklad kladné (pravé) šikmosti
- Příklad záporné (levé) šikmosti
- Šikmost populace – vzorec a výpočet
- Šikmost vzorku -. Vzorec a výpočet
- Šikmost v programu SPSS
- Šikmost – důsledky pro analýzu dat
Pozitivní (pravá) šikmost Příklad
Vědec má 1,000 lidí vyplnilo několik psychologických testů. V případě testu 5 mají výsledky testu šikmost = 2,0. Níže je zobrazen histogram těchto skóre.
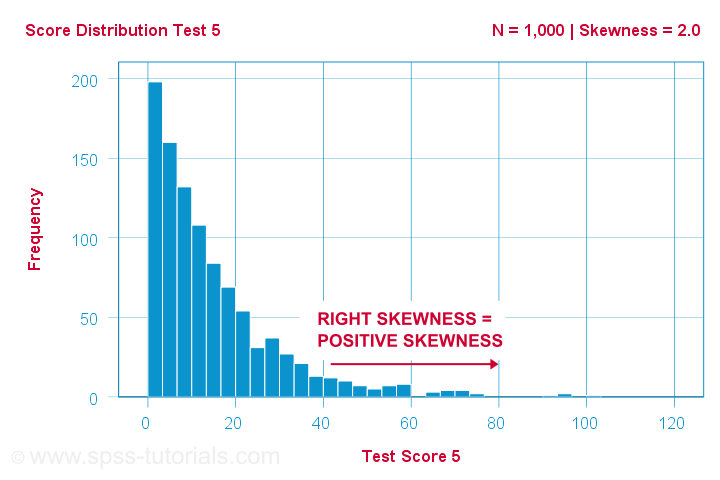
Histogram ukazuje velmi asymetrické rozdělení četností. Většina lidí dosáhla 20 bodů nebo méně, ale pravý chvost se táhne až k hodnotě kolem 90 bodů. Toto rozdělení je pravostranné.
Posuneme-li se po ose x doprava, dostaneme se z 0 na 20 až 40 bodů a tak dále. Směrem k pravé části grafu se tedy skóre stávají pozitivnějšími. Pravá šikmost je tedy kladná šikmostcož znamená šikmost > 0. Tento první příklad má šikmost = 2,0, jak je uvedeno v pravém horním rohu grafu. Skóre jsou silně kladně zkreslená.
Záporná (levá) šikmost Příklad
Další proměnná -skóre v testu 2- se ukáže, že má šikmost = -1,0. V tomto případě se jedná o zápornou šikmost. Jejich histogram je zobrazen níže.

Převážná část skóre se nachází v rozmezí 60 až 100 nebo podobně. Levý chvost je však poněkud roztažen. Toto rozdělení je tedy levostranné.
Vpravo: vlevo, vlevo. Pokud sledujeme osu x doleva, pohybujeme se směrem k zápornějším skóre. Proto je levá šikmost záporná. a skutečně, šikmost = -1,0 pro tato skóre. Jejich rozdělení je levostranné. Je však méně zkosené -nebo více symetrické- než náš první příklad, který měl šikmost = 2,0.
Symetrické rozdělení implikuje nulovou šikmost
Nakonec, symetrická rozdělení mají šikmost = 0. Skóre v testu 3 -která mají šikmost = 0,1- se tomu blíží.

Nyní pozorovaná rozdělení jsou zřídka přesně symetrická. To se většinou projevuje u některých teoretických výběrových rozdělení. Některé příklady jsou
- (standardní) normální rozdělení;
- rozdělení t a
- binomické rozdělení, pokud p = 0,5.
Všechna tato rozdělení jsou přesně symetrická, a mají tedy šikmost = 0.000…
Šikmost populace – vzorec a výpočet
Pokud chcete vypočítat šikmost pro jednu nebo více proměnných, nechte výpočet na nějakém softwaru. Ale -jen pro úplnost- přesto uvedu vzorce.
Pokud vaše data obsahují celou populaci, vypočítejte populační šikmost jako:
$$Populace\;skewness = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$$
kde
- \(X_i\) je každé individuální skóre;
- \(\mu\) je populační průměr;
- \(\sigma\) je populační směrodatná odchylka a
- \(N\) je velikost populace.
Pro příklad výpočtu pomocí tohoto vzorce viz tento Googlesheet (zobrazený níže).
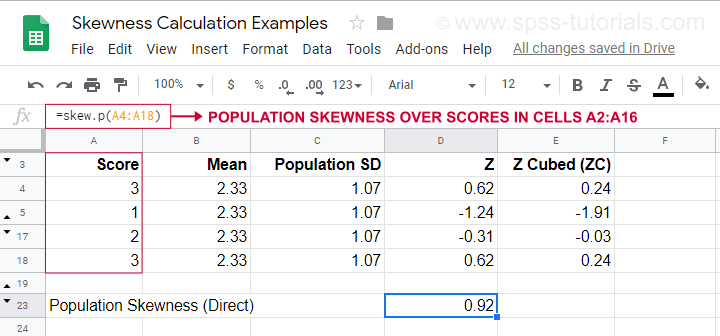
Ukazuje také, jak získat populační šikmost přímo pomocí=SKEW.P(…)kde „.P“ znamená „populace“. To potvrzuje výsledek našeho ručního výpočtu. Bohužel ani SPSS, ani JASP nepočítají populační šikmost: oba programy jsou omezeny na výběrovou šikmost.
Šikmost vzorku – vzorec a výpočet
Pokud vaše data obsahují prostý náhodný vzorek z nějaké populace, použijte
$$vzorek\;šikmost = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$
kde
- \(X_i\) je každé jednotlivé skóre;
- \(\overline{X}\) je výběrový průměr;
- \(S\) je výběrová směrodatná odchylka a
- \(N\) je velikost vzorku.
Příklad výpočtu je uveden v tomto Googlesheetu (zobrazen níže).
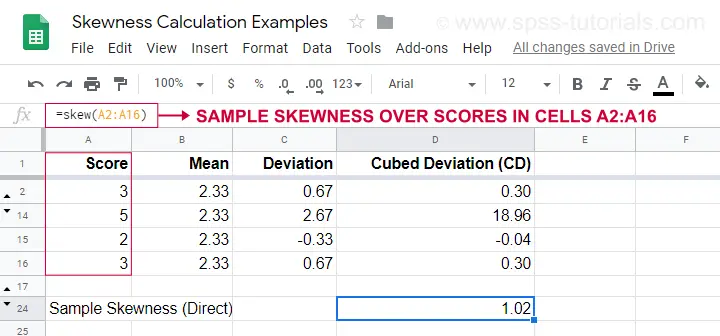
Snadnější možností pro získání výběrové šikmosti je použití=SKEW(…).což potvrzuje výsledek našeho ručního výpočtu.
Šikmost v SPSS
Předně, „šikmost“ v SPSS se vždy vztahuje ke šikmosti vzorku: tiše předpokládá, že vaše data obsahují vzorek, nikoli celou populaci. Existuje spousta možností, jak ji získat. Můj oblíbený je prostřednictvím MEANS, protože syntaxe a výstup jsou čisté a jednoduché. Níže uvedené snímky obrazovky vás jimi provedou.

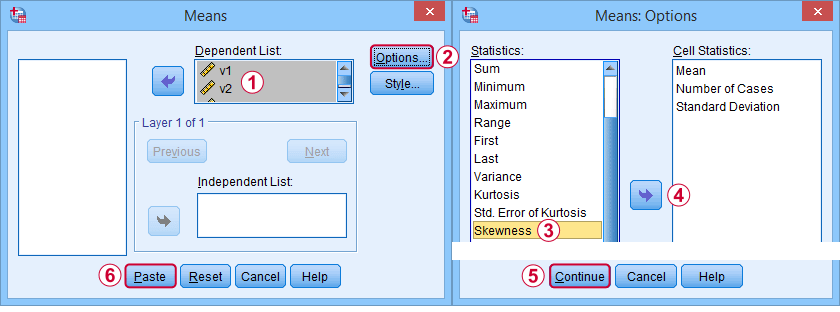
Syntaxe může být stejně jednoduchá jakomeans v1 to v5
/cells skew. velmi kompletní tabulka -včetně průměrů, směrodatných odchylek, mediánů a dalších údajů- se spustí zmeans v1 to v5
/cells count min max mean median stddev skew kurt.Výsledek je uveden níže.
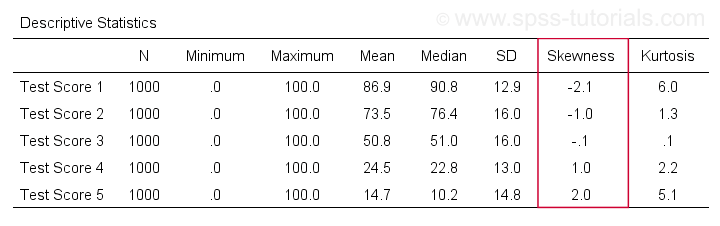
Šikmost – důsledky pro analýzu dat
Mnoho analýz -ANOVA, t-testy, regrese a další- vyžaduje předpoklad normality: proměnné by měly být v populaci normálně rozloženy. Normální rozdělení má šikmost = 0. Takže pozorování značné šikmosti v některých datech vzorku naznačuje, že předpoklad normality je porušen.
Takové porušení normality není problémem pro velké velikosti vzorku – řekněme N > 20 nebo 25 nebo tak nějak. V takovém případě je většina testů vůči takovému porušení robustní. To je dáno centrální limitní větou. Stručně řečeno, pro velké velikosti vzorků nepředstavuje šikmost
pro statistické testy žádný skutečný problém. šikmost je však často spojena s velkými směrodatnými odchylkami. Ty mohou mít za následek velké směrodatné chyby a nízkou statistickou sílu. Stejně tak může značná šikmost snížit šanci na zamítnutí některé nulové hypotézy, aby se prokázal nějaký účinek. V tomto případě může být neparametrický test moudřejší volbou, protože může mít větší sílu. porušení normality představuje skutečnou hrozbu
pro malé velikosti vzorku -řekněme- N < 20 nebo více. Při malých velikostech vzorků není mnoho testů odolných proti porušení předpokladu normality. Řešením je -opět- použití neparametrického testu, protože ty normalitu nevyžadují.
V neposlední řadě neexistuje žádný statistický test pro zkoumání, zda šikmost populace = 0. Nepřímým způsobem testování je test normality, například
- Kolmogorov-Smirnovův test normality a
- Shapiro-Wilkův test normality.
Když je však normalita skutečně potřebná -při malých velikostech vzorků-, mají takové testy malou sílu: nemusí dosáhnout statistické významnosti, i když jsou odchylky od normality závažné. Stejně tak poskytují především falešný pocit bezpečí.




