Lexikon odstředivých čerpadel
Ztráty výšky jsou důsledkem tření stěn ve všech typech potrubí a místního odporu proti proudění, například ve ventilech a armaturách (viz také Tlakové ztráty).
Doporučené rychlosti proudění
- Pro studenou vodu:
Sací potrubí 0.7-1,5 m/s
Výtlačné potrubí 1,0-2,0 m/s - Pro horkou vodu:
Sací potrubí 0,5-1,0 m/s
Výtlačné potrubí 1,5-3,5 m/s
Rovnice pro ztrátu výšky průtoku v přímé délce potrubí s kruhovým průřezem je:
λ Součinitel tření v potrubí
L Délka potrubí v m
d Vnitřní průměr potrubí v m
v Rychlost proudění v průřezu v m/s
(= 4 Q / π d2 s Q v m3/s)
g Tíhové zrychlení v m/s2
viz obr. 1 a 4 Ztráta výšky
Součinitel tření v potrubí byl stanoven experimentálně. Závisí pouze na stavu proudění zpracovávané kapaliny a na relativní drsnosti (d/k) potrubí, kterým kapalina protéká. Pro nekruhové průřezy potrubí platí ekvivalentní průměr v kapalinomechanickém vyjádření (d):
A Průřez v m2
U Obvod smáčeného průřezu v m
(volný povrch otevřeného kanálu se neuvažuje)
Stav proudění je určen Reynoldsovým číslem (Re) podle zákonů příbuznosti. Pro kruhové potrubí platí:
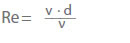
v Rychlost proudění v průřezu v m/s
(= 4 Q / π d2 s Q v m3/s)
ν Kinematická viskozita v m2/s
(pro vodu při 20 °C: 1.00 – 10 – 6 m2/s)
d Vnitřní průměr potrubí v m
Viz obr. 4 Ztráta výšky
Pro hydraulicky hladké potrubí, jako je hladké tažené kovové nebo plastové potrubí (např. PE nebo PVC), nebo v případě laminárního proudění lze vypočítat součinitel tření v potrubí (λ). Pro laminární proudění v potrubí s Reynoldsovým číslem menším než 2320 je součinitel tření v potrubí nezávislý na drsnosti:
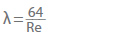
Je-li proudění turbulentní nebo Reynoldsovo číslo vyšší než 2320, lze součinitel tření v hydraulicky hladkém potrubí znázornit empirickou rovnicí podle Ecka (vzhledem k tomu, že odchylky jsou nižší než 1 %, je-li Reynoldsovo číslo nižší než 108).
Faktor tření v potrubí (λ) závisí také na dalším bezrozměrném parametru, tj. na relativní drsnosti vnitřního povrchu potrubí (d/k). Oba se musí uvádět ve stejné jednotce (např. mm).
Viz obr. 1 Ztráta výšky
(k) je střední absolutní drsnost vnitřního povrchu trubky, pro kterou jsou k dispozici přibližné hodnoty v závislosti na materiálu a výrobních postupech. Viz obr. 2 Ztráta výšky
Obr. 2 Ztráta výšky: Odhady středních výšek od vrcholu k údolí k (absolutní drsnost) potrubí
Více než mezní křivka, součinitel tření v potrubí (λ) závisí pouze na relativní drsnosti potrubí (d/k). Viz obr. 1 Ztráta výšky
Pro tuto oblast lze použít následující Moodyho empirickou rovnici:
Pro praktické použití je na obrázku znázorněna ztráta výšky (HL) na 100 m přímého ocelového potrubí jako funkce průtoku (Q) a vnitřního průměru potrubí (d).
Viz obr. 3 Ztráta výšky
Uvedené hodnoty platí pouze pro studenou, čistou vodu nebo pro kapaliny se stejnou kinematickou viskozitou, pro zcela zaplněné potrubí a pro absolutní drsnost vnitřního povrchu potrubí k = 0.05 mm.
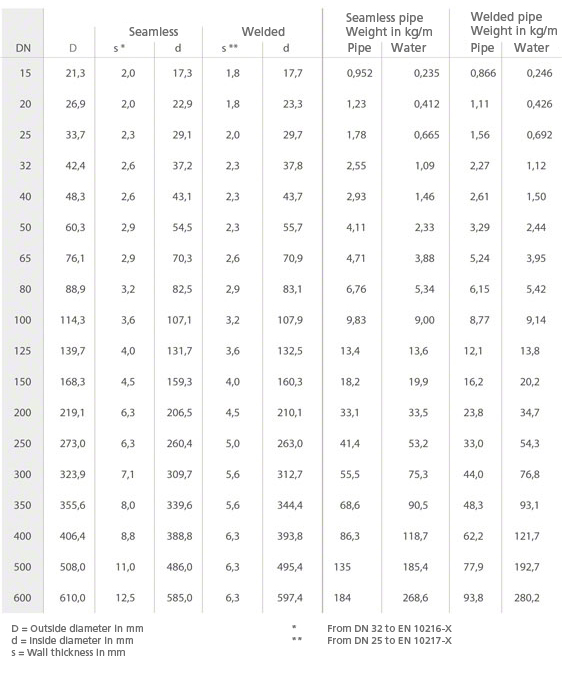
Rozměry, hmotnosti, naplnění vodou pro nové bezešvé nebo podélně svařované ocelové trubky
Viz příloha, Ztráta výšky, obr. 4
Vliv zvýšené drsnosti povrchu k bude demonstrován v následujícím textu pro často používaný soubor rozsahů parametrů (jmenovitý průměr DN = 50 až 300, rychlost proudění v = 0,8 až 3,0 m/s). Viz obr. 3 Ztráta výšky
Světle modrá oblast odpovídá podobně označené oblasti pro absolutní střední drsnost k = 0,05 mm.
Viz obr. 1 Ztráta výšky
Při drsnosti zvýšené šestinásobně (mírně inkrustovaná stará ocelová trubka s k = 0,30 = 300 μm (0.30 mm) jsou součinitele tření potrubí (a s tím související poměrné ztráty výšky) v tmavě modré oblasti pouze o 25 – 60 % vyšší než dříve.
Viz obr. 1 Ztráty výšky
U kanalizačního potrubí je třeba vzít v úvahu zvýšenou drsnost způsobenou znečištěním. U potrubí vystaveného extrémní inkrustaci lze skutečnou výškovou ztrátu určit pouze experimentálně. Odchylky od jmenovitého průměru výrazně mění výškovou ztrátu, protože vnitřní průměr potrubí figuruje v rovnici na 5. mocnině.
Například zmenšení vnitřního průměru o 5 % vede ke zvýšení výškové ztráty až o 30 %. Proto je důležité, aby vnitřní průměr nebyl ve výpočtech jednoduše nahrazen jmenovitým průměrem.
Ztráty výšky v plastových trubkách nebo hladkých tažených kovových potrubích jsou díky hladkému povrchu trubek velmi nízké. Stanovené ztráty výšky platí pro vodu o teplotě 10 °C. Při jiných teplotách je třeba ztráty u plastových trubek vynásobit stanoveným teplotním korekčním součinitelem, aby se zohlednila jejich větší tepelná roztažnost. U odpadní nebo jiné neupravené vody je třeba zohlednit další 20-30% ztrátu výšky pro případné usazeniny.
Ztráty výšky pro plastové a hladké tažené kovové trubky
Viz příloha, Ztráta výšky, obr. 1. 5
Ztráty hlavy v armaturách a tvarovkách
Ztráta hlavy (HL) v armaturách a tvarovkách je dána:
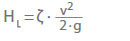
ζ Součinitel ztráty
Viz obr. 6 až 12 Ztráta výšky
v Rychlost proudění v charakteristickém průřezu A
(např. u trysky) v m/s
g Tíhové zrychlení 9,81 m/s2
Obr. 6 Ztráta výšky: Schéma provedení ventilů
Obr. 11 Ztráta výšky: Vliv zaoblení vnitřní a vnější strany kolen ve čtvercovém potrubí na součinitel ztrát ζ
Obr. 12 Ztráta výšky: Součinitele ztrát ζ pro šoupátka, kulové kohouty a šoupátka v závislosti na stupni otevření
Ztráty připadající na usměrnění poruch proudění na délce potrubí odpovídající 12 x DN za ventilem jsou zahrnuty do součinitelů ztrát podle směrnice VDI/VDE 2173. Hodnoty platí pro ventily, které mají ustálený nájezdový průtok, jsou plně otevřené a provozované se studenou vodou. V závislosti na podmínkách vstupního a výstupního průtoku, modelech ventilů a cílech vývoje (tj. levné nebo energeticky úsporné ventily) se mohou hodnoty ztrát výrazně lišit. Viz příloha, Ztráta hlavy, obr. 7
Při výpočtu tlakové ztráty vody ve ventilech se často místo ztrátového součinitele (ζ) používá hodnota kv:
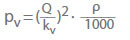
Hodnota kv je průtok v m3/h, který by vznikl při poklesu tlaku pv = 1 bar přes ventil pro studenou vodu. Popisuje závislost mezi tlakovou ztrátou (pL) v barech a průtokem (Q) v m3/h. Přepočet na součinitel průtoku ζ pro studenou vodu:
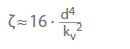
d Referenční (jmenovitý) průměr armatury v cm
Pro výpočet ztrát výšky v armaturách, odbočkách a adaptérech je třeba použít jiný přístup. Viz obr. 9 a 10 Ztráta hlavy
Obr. 9 Ztráta hlavy: Ztrátové součinitele ζ pro tvarovky 
Obr. 10 Ztráta hlavy: U všech armatur je třeba rozlišovat mezi dvěma formami tlakové ztráty
:
- Vratné tlakové ztráty (snížení tlaku)
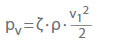
pv Tlaková ztráta v Pa
ζ Ztrátový součinitel
ρ Hustota v kg/m3
v Rychlost proudění v křiž.průřezu v m/s
- Vratné tlakové změny proudění bez tření podle Bernoulliho rovnice
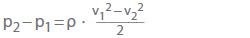
Při zrychleném proudění, např. při zmenšení průměru potrubí, (p2 – p1) je vždy záporná; pro zpomalené proudění, jako je rozšiřování potrubí, je vždy kladná. Při výpočtu čisté změny tlaku jako aritmetického součtu pL a (p2 – p1) je třeba vždy odečíst nevratné tlakové ztráty.
Vliv vysoce viskózních tekutin na charakteristickou křivku systému
Jelikož si zákony dynamiky tekutin zachovávají platnost pro všechny newtonovské tekutiny, jsou rovnice a diagramy pro výpočet součinitelů tření v potrubí a součinitelů ztrát pro ventily použitelné i pro viskózní tekutiny s vyšší viskozitou než voda.
Při výpočtu Reynoldsova čísla Re = v – d / ν , je třeba jednoduše nahradit kinematickou viskozitu viskózních tekutin νz za viskozitu vody νz.
Tím získáme nižší Re číslo a podle obr. 1 Ztráty hlavy větší součinitel tření v potrubí λz (Poznámka: vliv drsnosti stěn lze nyní často zanedbat, protože tloušťka mezní vrstvy v proudění je větší).
Všechny tlakové ztráty v potrubí a ventilech vypočtené pro vodu je třeba extrapolovat pomocí poměru λz/λw.
Obrázek 13 Ztráta hlavy je vhodný i pro obecné praktické použití: součinitel tření v potrubí λz lze rychle určit jako funkci průtoku Q, vnitřního průměru potrubí d a kinematické viskozity νz. Je však třeba mít na paměti, že součinitel λw v tomto diagramu platí pouze pro hydraulicky hladké potrubí (tj. nikoli pro drsné potrubí)! Odpovídající λw lze použít k výpočtu poměru λz/λw.
Jelikož statická složka charakteristické křivky systému Hsys , viz obr. 1 Charakteristická křivka systému a obr. 2 Hlava, není ovlivněna viskozitou, lze dynamickou složku charakteristické křivky systému pro vodu překreslit jako strmější parabolu pro viskózní kapalinu.
Vliv nenewtonských kapalin na charakteristickou křivku systému
Protože křivky proudění nejsou přímky s konstantní lineární viskozitou, je výpočet ztrát výšky velmi těžkopádný. V tomto případě je výpočet ztrát založen na zkušenostech s konkrétními kapalinami
.