Metoda syntetického dělení
Musím říct, že syntetické dělení je nejzábavnější způsob dělení mnohočlenů. Oproti metodě dlouhého dělení polynomů má méně kroků k dosažení odpovědi. V této lekci proberu pět (5) příkladů, které by vás snad měly seznámit se základními postupy při úspěšném dělení mnohočlenů pomocí syntetického dělení.
Nezapomeňte:
- Ujistěte se, že dividenda je ve standardním tvaru. To znamená, že mocniny jsou v sestupném pořadí.
- Dělitel musí být ve tvaru x – \levý( c \pravý).
Příklady, jak dělit mnohočleny pomocí syntetického dělení
Příklad 1. Dělení pomocí syntetického dělení: Dělíme níže uvedený polynom.
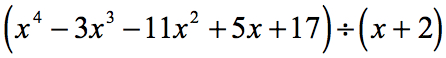
Přezkoumejme znovu danou úlohu a případně proveďme potřebné úpravy.
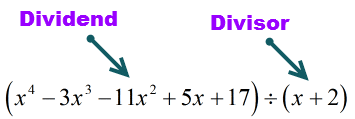
Dividenda (věc k dělení) je ve standardním tvaru, protože exponenty jsou v sestupném pořadí. To je dobře!
Dělitele je třeba přepsat jako
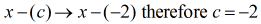
V tuto chvíli již mohu nastavit syntetické dělení vytažením koeficientů dividendy a jejich seřazením nahoru.
Přímo na levou stranu umístěte hodnotu c = – 2 dovnitř „krabice“.
Nakonec sestrojte vodorovnou čáru těsně pod koeficienty dividendy.
Kroky:
1. Dělíme na dvě části. Vypusťte první koeficient pod vodorovnou čáru.
2. Vynásobte toto vypuštěné číslo číslem v „rámečku“. Ať je jeho součin jakýkoli, umístěte ho nad vodorovnou čáru těsně pod druhý koeficient.
3. Sečtěte sloupec čísel a součet umístěte přímo pod vodorovnou čáru.
4. Postup opakujte, dokud vám nedojdou sloupce k sečtení.
Podívejte se na animované řešení níže:
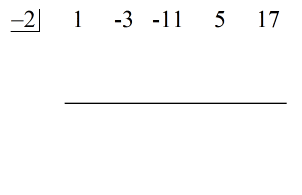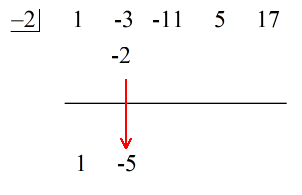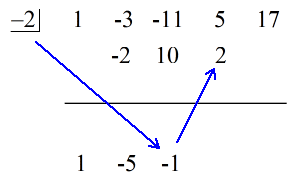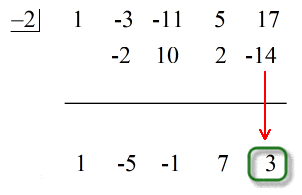
Poslední číslo pod vodorovnou čárou je vždy zbytek! Zbytek této úlohy je 3.
Jak tedy prezentujeme naši konečnou odpověď?
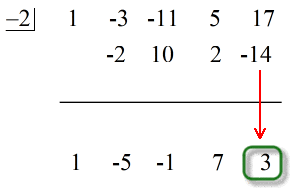
- Zobrazte svou konečnou odpověď ve tvaru
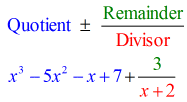
Všimněte si, že čísla pod vodorovnou čarou kromě posledního (zbytku) jsou koeficienty kvocientu.
Ještě více, že exponenty proměnných kvocientu jsou všechny redukovány o 1.
Příklad 2. Jaký je výsledek?
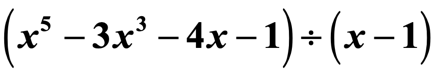
Tato otázka není záludná. Všimněte si, že v kvocientu nejsou všechny exponenty proměnné x.
Vidím, že nám chybí {x^4} a {x^2}. Abychom zahrnuli všechny koeficienty proměnné x v klesající mocnině, měli bychom původní úlohu přepsat takto. K těmto chybějícím x připojíme nuly. Také dělitele vyjádříme jako x – (c), což jasně prozrazuje hodnotu c, tedy c = + 1.
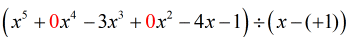
Od tohoto okamžiku mohu nyní nastavit čísla, abychom mohli pokračovat v postupu.
Kroky:
1. Vypusťte první koeficient pod vodorovnou čáru.
2. Vynásobte toto vypuštěné číslo číslem v „rámečku“. Ať už je jeho součin jakýkoli, umístěte ho nad vodorovnou čáru těsně pod druhý koeficient.
3. Sečtěte sloupec čísel a součet umístěte přímo pod vodorovnou čáru.
4. Postup opakujte, dokud vám nedojdou sloupce k sečtení.
Podívejte se na animované řešení níže:
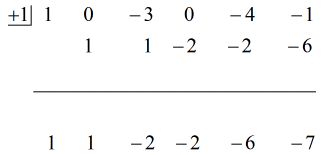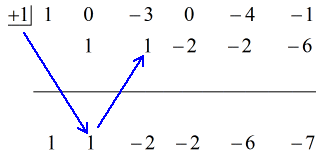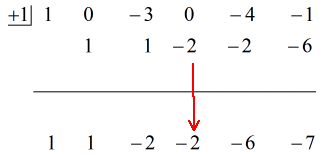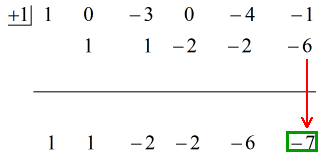
Takto dosadíme konečnou odpověď ve tvaru
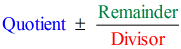
máme
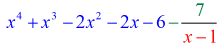
Příklad 3: Rozdělte níže uvedený polynom.
\left( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Tohle začíná být zajímavější! Kvocient rozhodně vypadá hrozně, protože v něm hodně chybí. Nejenže v něm chybí některá x, což jsou {x^3} a {x^2}, ale chybí i konstanta.
Chci-li to napravit, přepíšu původní úlohu tak, aby v ní byla započítána všechna x. Vždyť je to tak, že v ní není žádné x. Ale hlavně nezapomeňte započítat chybějící konstantu, která je nulová.
„Nová a vylepšená“ úloha by měla vypadat takto:
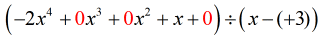
Odtud pokračujte v krocích jako obvykle.
Kroky:
1. Problém je třeba vyřešit tak, že se do něj započte konstanta, která je nulová. Vypusťte první koeficient pod vodorovnou čáru.
2. Vynásobte toto vypuštěné číslo číslem v „rámečku“. Ať už je jeho součin jakýkoli, umístěte ho nad vodorovnou čáru těsně pod druhý koeficient.
3. Sečtěte sloupec čísel a součet umístěte přímo pod vodorovnou čáru.
4. Postup opakujte, dokud vám nedojdou sloupce k sečtení.
Podívejte se na animované řešení níže:
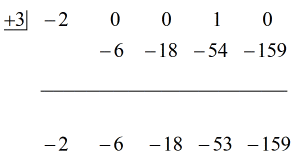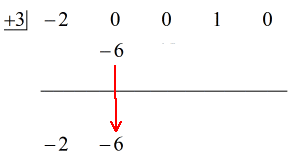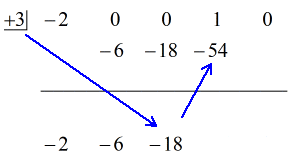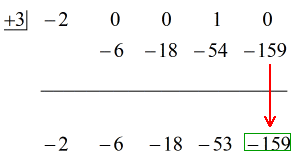
Konečná odpověď na tuto otázku je tedy
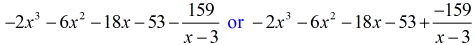
Konečnou odpověď můžete zapsat dvěma způsoby. Prvním z nich je použití symbolu mínus nebo odčítání, který označuje, že zbytek je záporný. Druhým je použití symbolu +, ale připojení záporného symbolu k čitateli. Znamenají totéž!
Příklad 4: Rozdělte níže uvedený polynom.
\levá( { – {x^5} + 1} \pravá) \div \levá( {x + 1} \pravá)
Nenechte se tímto problémem odradit. Je to vlastně docela snadné, zvláště teď, když už jste si prošli několik příkladů. Vždy nezapomeňte „doplnit chybějící části“, že?“
Podívejte se na dividendu a měli byste souhlasit, že chybějícími částmi jsou {x^4}, {x^3}, {x^2} a x.
Přepisem původní úlohy, která je připravena k syntetickému dělení, dostaneme…
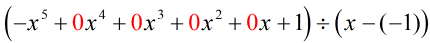
Naplníme chybějící x nulami a explicitně vyřešíme c = -1.
Kroky:
1. Zjistěte, co je to c? Vypusťte první koeficient pod vodorovnou čáru.
2. Vynásobte toto vypuštěné číslo číslem v „rámečku“. Ať už je jeho součin jakýkoli, umístěte ho nad vodorovnou čáru těsně pod druhý koeficient.
3. Sloupec čísel sečtěte a součet umístěte přímo pod vodorovnou čáru.
4. Sloupec čísel sečtěte a součet umístěte přímo pod vodorovnou čáru. Postup opakujte, dokud vám nedojdou sloupce k sečtení.
Podívejte se na animované řešení níže:
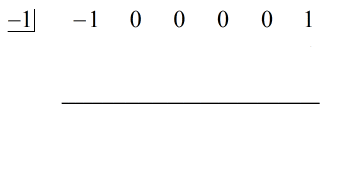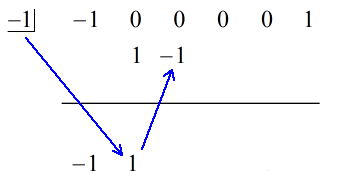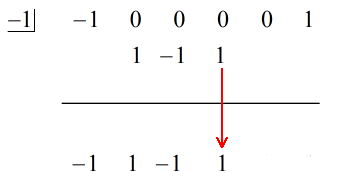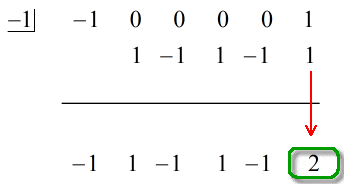
Poslední číslo pod vodorovnou čarou bude vždy zbytek. Nezapomeňte na to. V tomto případě je zbytek roven 2.
Naše konečná odpověď je
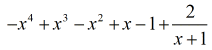
Příklad 5: Dělení polynomu dvojčlenem.
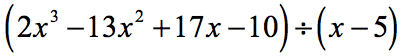
V tomto příkladu dostaneme zbytek nula. Když se tak stane, dělitel se stane činitelem dividendy. Jinými slovy, dělitel rovnoměrně dělí dividendu.
Při zkoumání úlohy vidím, že v ní nechybí žádné složky. Všechny mocniny x jsou zohledněny a máme konstantu. To je skvělé! Tato úloha je ve skutečnosti připravena k syntetickému dělení.
Kroky:
1. Vypusťte první koeficient pod vodorovnou čáru.
2. Vynásobte toto vypuštěné číslo číslem v „rámečku“. Ať už je jeho součin jakýkoli, umístěte ho nad vodorovnou čáru těsně pod druhý koeficient.
3. Sečtěte sloupec čísel a součet umístěte přímo pod vodorovnou čáru.
4. Postup opakujte, dokud vám nedojdou sloupce k sečtení.
Podívejte se na animované řešení níže:
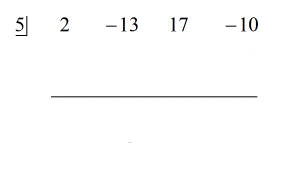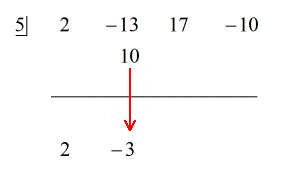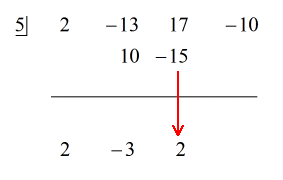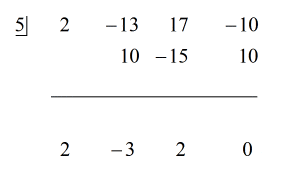
Protože zbytek je roven nule, to znamená, že dělitel x – 5 je dělitelem dividendy
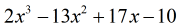
tudíž
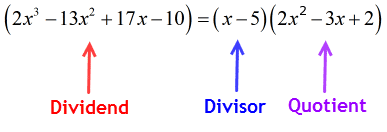
Cvičení s pracovními listy
Mohlo by vás také zajímat:
Sčítání a odčítání mnohočlenů
Dělení mnohočlenů metodou dlouhého dělení
Násobení dvojčlenů metodou FOIL
Násobení mnohočlenů




