Rovnice relativistické a kvantové mechaniky (bez spinu)
Úvod
Pochybovat o všem nebo věřit všemu jsou dvě stejně pohodlná řešení;
obě se obejdou bez nutnosti reflexe.
Henri Poincaré (1854-1912)
Vím, vím, ale předpokládejme – jen předpokládejme! – čistota kruhu nás zaslepila, abychom neviděli nic mimo něj!
Musím začít úplně od začátku s novýma očima, musím všechno přehodnotit!
Hypathia (∼360-415 n. l.)
V roce 1913 Bohr na základě Balmerových empirických vzorců zkonstruoval model atomu založený na kvantování orbitálního momentu hybnosti , který byl následně doplněn obecnějšími Sommerfeldovými kvantovacími pravidly. V těchto letech se přirozeně nepředpokládala přítomnost spinu nebo vlastního magnetického momentu částice nebo zejména spin-orbitální interakce, případně interakce s jaderným spinem.
V roce 1916 Sommerfeld v rámci relativistických přístupů odvodil vzorec pro energetické hladiny atomu podobného vodíku, aniž by bral v úvahu spin . Sommerfeld vycházel z modelu Bohrova atomu a použil relativistický vztah mezi hybností pand energií Evolné částice o hmotnosti m.
kde cis je rychlost světla.
Ve vnějším poli se čtyřrozměrným potenciálem (φ,A) se předpokládalo, že pro částici s nábojem qtento vztah lze také použít, pokud od výrazu pro zobecněnou hybnost částice odečteme složky čtyřrozměrného momentu hybnosti pole (qφ,qA):
V případě Coulombova potenciálu φ=Ze/r, kde e je náboj elektronu, ris vzdálenost od jádra a Zje atomové číslo, dostáváme ve sférických souřadnicích
kde Lis úhlový moment hybnosti. Bohrovy-Sommerfeldovy kvantovací podmínky mají tvar
kde nφa nra jsou orbitální, resp. radiální kvantová čísla. Pro energetické hladiny získal Sommerfeld vzorec
kde hlavní kvantové číslo n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1 a α=1/137,036je konstanta jemné struktury. V článku publikovaném v roce 1916 však Sommerfeld „udělal šťastnou chybu“ a odvozený vzorec uvedl v následujícím tvaru
Ve vzorci (6) byly dokonale popsány všechny zvláštnosti struktury spektra vodíku a dalších podobných atomů s pro tehdejší léta limitní přesností měření a o správnosti samotného vzorce nebylo pochyb. Proto byl Sommerfeldův vzorec vnímán jako empirický a místo kvantového čísla l se v něm objevilo „tajemné“ vnitřní kvantové číslo s polocelými hodnotami j=1/2,3/2,5/2,….,n+1/2byl zaveden vzorec (6) v zobrazení
kde n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2 a l má hodnoty l=0při j=1/2a l=j±1/2pro ostatní. Tento vzorec se shoduje s výsledkem přesného řešení relativistických Diracových rovnic v roce 1928 pro částici se spinem 1/2s klasickým výrazem pro potenciální energii nepohyblivého náboje v Coulombově poli jádra s atomovým číslem Zve tvaru Ur=Ze2/r.
Vzorce (7) také naznačil zvláštní omezení hodnoty náboje jádra s atomovým číslem Z<137, nad kterým vzorec ztrácí smysl. Bylo také zřejmé, že v rámci nastíněných přístupů, silné a gravitační interakce, nejsou popsány pohyby planet. Problém Z<137nebo α>1zůstává nevyřešeným problémem relativistické kvantové mechaniky. Rozšíříme-li vzorec (7) přes řád mocnin Zα2v Taylorově řadě s přesností rozšíření až na členy o mocniny Zα6, dostaneme
V letech 1925-1926 pracoval Schrödinger na odvození rovnice pro vlnovou funkci částice popisující De Broglieho vlny . Odvození rovnice bylo rovněž založeno na relativistickém vztahu (1) mezi hybností a energií Ečástice, který prezentoval pomocí operátorů čtverců energie a hybnosti ve formě rovnice pro vlnovou funkci
podobně jako Sommerfeld, Schrödinger používal pro částici ve vnějším poli následující zobrazení
V případě stacionárních stavů a. nabité částice v poli Coulombova potenciálu pro atom vodíku bylo nutné řešit rovnici
Jak je vidět, kvadratický výraz potenciální energie q2φ2r/2mc2je v rovnici přítomen s kladným znaménkem a v případě přitažlivých polí vede řešení k určitým obtížím. Při přiblížení k bodu singularity se v důsledku záporného znaménka zvyšují přitažlivé síly a přítomnost singularity vede ke známým omezením velikosti interakcí (obrázek 1).
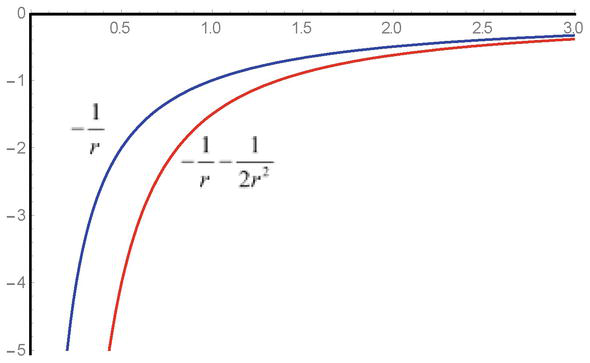
Obrázek 1.
Závislost vzorku potenciálu přitažlivého pole-1/ a energie potenciální interakce-1/r-1/2r2v Kleinových-Gordonových rovnicích.
Dále je vlnový vektor kis reprezentován jako
a při uvažování problému průchodu částice s energií EthPřes potenciální bariéru U=qφr(obr. 2), jejíž výška je větší než dvojnásobná klidová energie částice U>2mc2 , nabývá koeficient přenosu hodnoty jednoty bez ohledu na výšku bariéry (Kleinův paradox) .
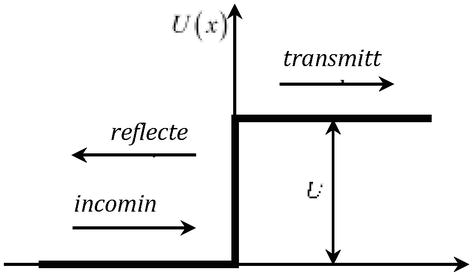
Obrázek 2.
Průchod částice potenciální bariérouU.
Další potíž spočívá v tom, že jak ukazuje řešení problému částic v potenciálové jámě, v dostatečné hloubce může částice s vlnovou délkou ƛ=ℏ/mc mít vázané stavy (může být lokalizována) v jámě o šířce menší, než je vlnová délka částice d<ƛ/2(obr. 3), což odporuje základnímu principu kvantové mechaniky – Heisenbergovu principu neurčitosti.
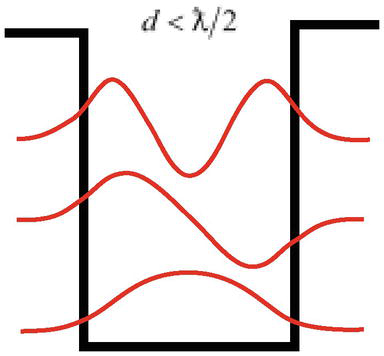
Obrázek 3.
Částici s vlnovou délkoƛ lze lokalizovat v jamce o šířced<ƛ/2. To znamená, že částice s vlnovou délkoƛ může být lokalizována v jamce o šířced<ƛ/2.
Také řešení úlohy atomu podobného vodíku je omezeno hodnotou pořadového čísla atomového jádra Z≤68(pro Diracovu rovnici je omezení atomového čísla Z≤137). Totéž v relativistické mechanice-při uvažování silných interakcí řešení Hamiltonovy-Jacobyho relativistické rovnice udává takzvaný „pád částice na střed“ .
S cílem zbavit se kvadratického členu nebo obrátit jeho znaménko bylo v posledních letech navrženo reprezentovat potenciální energii v Klein-Gordonově a Diracově rovnici jako rozdíl čtverců z vyjádření skalárního a vektorového potenciálu (S-vlnová rovnice) . Takový matematický formalismus situaci koriguje, ale z fyzikálního hlediska nejsou takové reprezentace nijak opodstatněné a pole odpovídající takovým pseudopotenciálům v přírodě neexistují.
Ještě horší je to s přítomností kvadratického členu vektorového pole, kvůli jehož znaménku dostáváme v přírodě neexistující stavy a řešení, která odporují zkušenosti.
Podle řešení rovnic kvantové mechaniky a Hamilton-Jacobyho, ukazuje, že nabitá částice v magnetickém poli má kromě rotace po kružnici také radiální vibrace-Landauovy hladiny (a to i v případě nulové orbitální hybnosti).
Za těch 90 let, zejména při velmi přesných experimentech s cyklotronovou rezonancí, nikdo nezjistil radiální vibrace elektronů a Landauovy hladiny.
Řešením této rovnice dostal Schrödinger stejně jako Sommerfeld vzorec (5), který ne zcela přesně popisoval strukturu vodíkového spektra. Navíc z řešení úlohy pro částici v potenciálové jámě vyplývá, že částice s vlnovou délkou ƛ=ℏ/mchas vázané stavy (je umístěna) v jámě libovolné velikosti a zejména mnohem menší než ƛ/2 . Tato skutečnost je v rozporu se základním principem kvantové (vlnové) teorie, principem neurčitosti.
V roce 1925 Schrödinger poslal tuto práci do redakce časopisu „Annalen der Physik“ , ale poté rukopis převzal, odmítl relativistické přístupy a v roce 1926 sestavil vlnovou rovnici na základě klasického Hamiltonova vyjádření, Schrödingerovu rovnici .
Rovnice popisovala spektrum atomu vodíku pouze kvalitativně, neměla však žádná nepřiměřená omezení nebo singulární řešení v podobě Sommerfeldova-Diracova vzorce. Klein , Fock a Gordon publikovali v roce 1926 relativistickou rovnici založenou na vlnové rovnici pro částici bez spinu; nazývá se Klein-Fock-Gordonova rovnice.
S objevem spinu se situace drasticky změnila a v roce 1926 Heisenberg a Jordan ukázali, že v rámci Pauliho popisu spinu elektronu je polovina energie spin-orbitální interakce rovna členu s mocninou α4 v Taylorově řadě rozšíření Sommerfeldovy rovnice odkaz jde sem.
Proč právě polovina, to se Thomas v roce 1927 pokusil vysvětlit přítomností relativistické precese elektronu ve vztažné soustavě pohybu po dráze . Energie Thomasovy precese je přesně rovna polovině hodnoty energie spin-orbitální interakce s inverzním (kladným) znaménkem, kterou je třeba přičíst k energii spin-orbitální interakce. Nesprávný předpoklad, že frekvence Thomasovy precese je v obou vztažných rámcích stejná, a neexistence společného a správného odvození pro neinerciální (rotující) vztažné rámce však vyvolaly pochybnosti o správnosti takových přístupů. Důvod výskytu poloviční energie spin-orbitální interakce v Sommerfeldově vzorci je stále předmětem zkoumání a je jedním z nevyřešených problémů moderní fyziky.
Na druhou stranu, jak při odvození Sommerfeldova vzorce, tak při řešení Kleinovy-Fockovy-Gordonovy rovnice pro problém atomu vodíku , nebyl původně brán v úvahu ani spin, ani energie spin-orbitální interakce. Proto získané jemné štěpení nemůže být v žádném případě způsobeno spin-orbitální interakcí. Jedná se o relativistický, ale čistě mechanický jev, kdy hmotnost (setrvačnost) částice již závisí na rychlosti pohybu po dráze (momentu hybnosti), kvůli kterému se mění radiální pohyb elektronu a naopak. Právě tato závislost, která vede k rozštěpení energetických hladin elektronu a k nemožnosti zavést pouze jedno, hlavní kvantové číslo. Nicméně i za tohoto předpokladu je pořadí štěpení hladin podle vzorce (8) v rozporu s logikou; ukazuje se, že čím větší je orbitální úhlový moment hybnosti, tím menší je energie štěpené hladiny.
Matrixová reprezentace vlny druhého řádu rovnice (8) je v rozporu s logikou. (9) soustavou rovnic prvního řádu je Diracova konstrukce relativistické elektronové rovnice (Diracovy matice jsou konkrétní reprezentací Cliffordových-Lipschitzových čísel ). Ve standardní reprezentaci má Diracova rovnice pro volnou částici tvar .
kde
jsou Pauliho matice (jednotková matice se ve vzorcích vynechává).
Pro částici ve vnějším poli platí rovnice. (16) obvykle zapisuje ve tvaru
kde pro invariantní zobrazení v případě volné částice jsou rovnice složeny pro rozdíl mezi zobecněnou hybností a hybností pole.
V případě potenciální energie nepohyblivého náboje v Coulombově poli dostaneme Sommerfeldův-Diracův vzorec jako výsledek přesného řešení této konkrétní rovnice. Tam se opět, i když pro systém se spinem 1/2nezohledňuje zpočátku energie spin-orbitální interakce, ale polovina se získá z přesného řešení úlohy atomu vodíku.
Přesnější Lambova měření v roce 1947 a následná vylepšení spektra atomu vodíku odhalila, že kromě čar s maximem j jsou všechny ostatní také rozděleny a poněkud posunuty (Lambův posun). Aby bylo možné sladit výsledky teorie s přesnějšími experimentálními údaji o spektru atomu vodíku, bylo třeba navrhnout jiná řešení a přístupy, než byly stanoveny odvozením Diracovy rovnice.
Nové teoretické přístupy nic nepřinesly a pouze doplnily teorii o nelogické a nefyzikální návrhy na překonání vznikající singularity řešení: renormalizace, konečný rozdíl nekonečen s požadovanou hodnotou rozdílu atd. Zohlednění velikosti jádra korigovalo pouze hodnotu Z na větší, ale problém Z>137nevyřešilo. Neuvěřitelný výsledek byl také získán pro problém atomu vodíku, že elektron se nachází s největší pravděpodobností ve středu atomu, tedy v jádře.
Výsledky řešení problému pro částici v potenciálové jámě jak v případě Kleinovy-Fockovy-Gordonovy rovnice, tak Diracovy rovnice odporují základnímu principu kvantové mechaniky, principu neurčitosti. Z řešení vyplývá, že částice může být ve vázaném stavu v jamce s libovolnými rozměry, zejména s rozměry mnohem menšími, než je vlnová délka samotné částice, A=ℏ/mc.
Přestože Dirac sám navrhl soustavu lineárních relativistických rovnic prvního stupně v maticovém zobrazení, které popisovaly systém se spinem 1/2, rozpory nezmizely a on sám zůstal s výsledky své teorie nespokojen. Jak Dirac napsal v roce 1956 , vývoj relativistické elektronové teorie lze nyní považovat za příklad toho, jak nesprávné argumenty někdy vedou k cennému výsledku. V 70. letech se ukázalo, že relativistická teorie kvantové mechaniky neexistuje a že je třeba hledat nové, fundamentální přístupy a rovnice pro konstrukci konzistentní teorie relativistické kvantové mechaniky. A v 80. letech již Dirac hovořil o nepřekonatelných obtížích stávající kvantové teorie a o nutnosti vytvořit teorii novou .
Důvod neúspěchu těchto teorií je poměrně jednoduchý – spočívá v ignorování závislosti energie interakce s polem na rychlosti částice. Zobecněná hybnost soustavy, částice plus vnější pole, je součtem relativistického výrazu pro mechanickou hybnost částice a hybnost pole v případě interakce s nehybnou částicí
což není invariantní zobrazení rychlosti částice. Pro konstrukci nějakého invariantu z takové reprezentace byl ve všech případech použit „invariantní“ vztah v podobě rozdílu mezi zobecněnou hybností systému a hybností pole v případě interakce s nehybnou částicí
Je zřejmé, že permutace složek zobecněného momentu hybnosti pro konstrukci invariantu neřeší zadaný problém. Tvrzení, že výraz (20) je mechanickou hybností částice, a proto je invariantem, je nedokazatelné a je třeba vzorec (20) uchopit jako empirický. Proto při vysokých rychlostech nebo silných interakcích dochází k nezohledněné závislosti energie interakce částice s polem na rychlosti pohybu částice, což vede k chybným výsledkům nebo nemožnosti výpočtů.
V , bylo navrženo invariantní zobrazení zobecněné hybnosti systému, kde byla zohledněna závislost energie interakce částice s polem na rychlosti:
což je čtyřrozměrné zobrazení zobecněné hybnosti soustavy založené na výrazu pro zobecněnou hybnost nepohyblivé částice v klidovém stavu
jehož invariant je vždy roven výrazu (19) bez ohledu na stav soustavy.
Použití variačních principů pro konstrukci relativistické a kvantové teorie bylo založeno na principech konstrukce mechaniky pomocí Lagrangiánu systému , který původně nebyl určen pro relativistické přístupy. Konstrukce Lagrangiánu je parametrická s jedinou časovou proměnnou τ = ct, vyčleněnou z proměnných čtyřrozměrného prostoru (ostatní jsou reprezentovány závislostí na této proměnné τ) a obsahuje celkový diferenciál vzhledem k této proměnné, rychlosti částice. Taková konstrukce je nepřijatelná z důvodu nemožnosti uplatnit princip invariance reprezentace proměnných a kovariantní reprezentace akce systému.
V , pro konstrukci relativistické teorie na základě variačních principů byla uvažována kanonická (neparametrická) řešení variační úlohy pro kanonicky definované integrální funkcionály a napsána kanonická řešení variačních úloh mechaniky v Minkowského prostorech. Díky sjednocení variačních principů nejmenší akce, toku a nadtoku byly získány kanonicky invariantní rovnice pro zobecněný moment hybnosti. Z těchto rovnic jsou získány výrazy pro akční funkci a vlnovou funkci jako obecné řešení sjednocené variační úlohy mechaniky.
Následují zobecněný princip invariance a odpovídající zobrazení zobecněného momentu hybnosti soustavy, rovnice relativistické a kvantové mechaniky , uvádíme řešení úloh pohybu náboje v konstantním elektrickém poli, úlohy pro částici v potenciálové jámě a průchodu částice potenciálovou bariérou, úlohy pohybu v exponenciálním poli (Morse), úlohy nabité částice v magnetickém poli a také jsou uvedeny úlohy atomu vodíku.
Následují zobecněný princip invariance a odpovídající zobrazení zobecněného momentu hybnosti soustavy.




