Skewness – Hurtig introduktion, eksempler og formler
Skewness er et tal, der angiver, i hvilken grad
en variabel er asymmetrisk fordelt.
- Positiv (højre) skævhed Eksempel
- Negativ (venstre) skævhed Eksempel
- Populationsskævhed – formel og beregning
- Stikprøve skævhed – formel og beregning
- Stikprøve skævhed – Formel og beregning
- Skewness i SPSS
- Skewness – implikationer for dataanalyse
Positiv (højre) Skewness Eksempel
En videnskabsmand har 1,000 personer gennemføre nogle psykologiske tests. For test 5 har testresultaterne en skewness = 2,0. Et histogram af disse resultater er vist nedenfor.
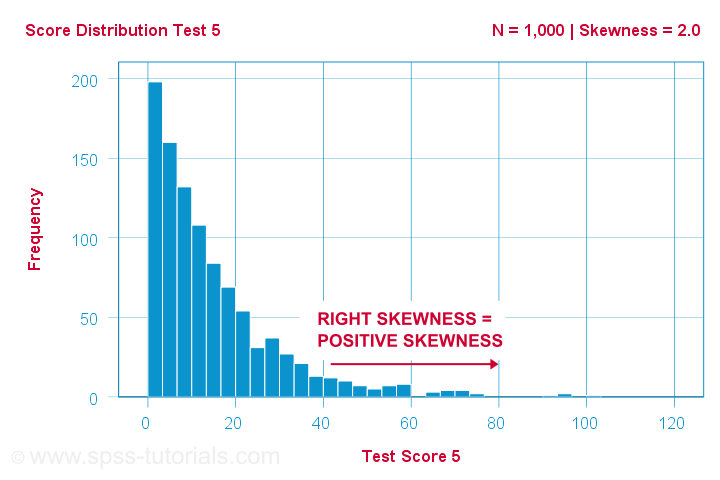
Histogrammet viser en meget asymmetrisk frekvensfordeling. De fleste scorer 20 point eller derunder, men den højre hale strækker sig op til 90 eller deromkring. Denne fordeling er højreskæv.
Hvis vi bevæger os mod højre langs x-aksen, går vi fra 0 til 20 til 40 point og så videre. Så mod højre i grafen bliver pointene mere positive. Derfor er højre skævhed positiv skævhedsom betyder skævhed > 0. Dette første eksempel har skævhed = 2,0, som angivet i det øverste højre hjørne af grafen. Scorerne er stærkt positivt skæve.
Negativ (venstre) skævhed Eksempel
En anden variabel -scorerne på test 2- viser sig at have skævhed = -1,0. Deres histogram er vist nedenfor.

Størstedelen af scorerne ligger mellem 60 og 100 eller deromkring. Den venstre hale er dog strakt noget ud. Så denne fordeling er venstre-skæv.
Højre: til venstre, til venstre, til venstre. Hvis vi følger x-aksen til venstre, bevæger vi os i retning af mere negative scorer. Det er derfor, at venstre skævhed er negativ skævhed.Og faktisk er skævhed = -1,0 for disse scorer. Deres fordeling er venstre skæv. Den er dog mindre skæv – eller mere symmetrisk – end vores første eksempel, som havde skewness = 2,0.
Symmetrisk fordeling indebærer nul skewness
Endeligt har symmetriske fordelinger skewness = 0. Scorerne i test 3 – med skewness = 0,1 – kommer tæt på.

Nu er observerede fordelinger sjældent præcist symmetriske. Dette ses mest for nogle teoretiske stikprøvefordelinger. Nogle eksempler er
- den (standard)normale fordeling;
- den t-fordeling og
- den binomiale fordeling, hvis p = 0,5.
Disse fordelinger er alle nøjagtigt symmetriske og har således skewness = 0.000…
Befolkningens skævhed – formel og beregning
Hvis du gerne vil beregne skævheder for en eller flere variabler, skal du bare overlade beregningerne til noget software. Men – blot for fuldstændighedens skyld – vil jeg alligevel nævne formlerne.
Hvis dine data indeholder hele din population, skal du beregne populationsskewness som:
$$$Population\;skewness = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$$$
hvor
- \(X_i\) er hver enkelt score;
- \(\mu\) er populationens gennemsnit;
- \(\sigma\) er populationens standardafvigelse og
- \(N\) er populationens størrelse.
For et beregningseksempel med denne formel henvises til dette Googlesheet (vist nedenfor).
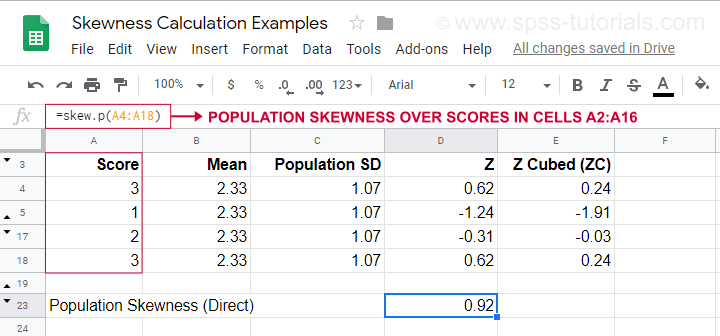
Det viser også, hvordan man kan få populationens skævhed direkte ved at bruge=SKEW.P(…)hvor “.P” betyder “population”. Dette bekræfter resultatet af vores manuelle beregning. Desværre beregner hverken SPSS eller JASP skævhed for populationen: begge er begrænset til skævhed for stikprøver.
Sample Skewness – formel og beregning
Hvis dine data indeholder en simpel tilfældig stikprøve fra en population, skal du bruge
$$$Sample\;skewness = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$$$
hvor
- \(X_i\) er hver enkelt score;
- \(\overline{X}\) er stikprøvens gennemsnit;
- \(S\) er stikprøvens standardafvigelse, og
- \(N\) er stikprøvens størrelse.
Et eksempel på en beregning er vist i dette Googlesheet (vist nedenfor).
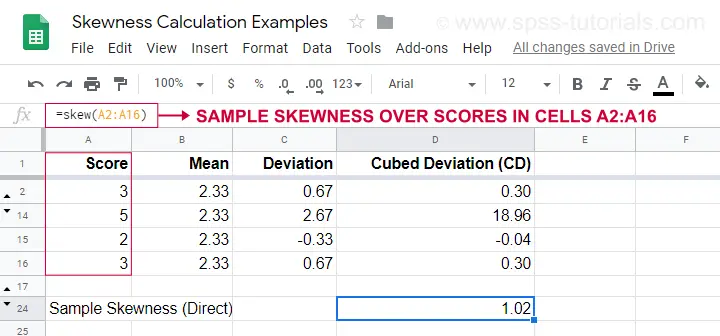
En nemmere mulighed for at opnå skævhed i stikprøven er at bruge=SKEW(…).hvilket bekræfter resultatet af vores manuelle beregning.
Skewness i SPSS
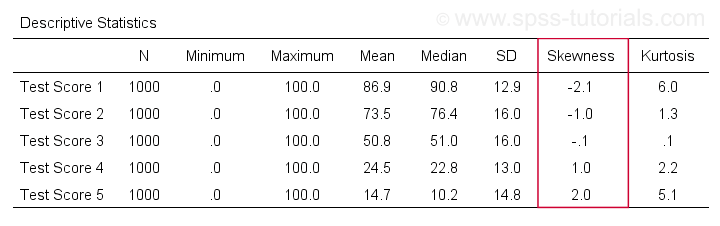
Først og fremmest henviser “skewness” i SPSS altid til stikprøveskewness: det forudsætter stille og roligt, at dine data indeholder en stikprøve og ikke en hel population. Der er masser af muligheder for at opnå det. Min favorit er via MEANS, fordi syntaksen og output er ren og enkel. Skærmbillederne nedenfor guider dig igennem.

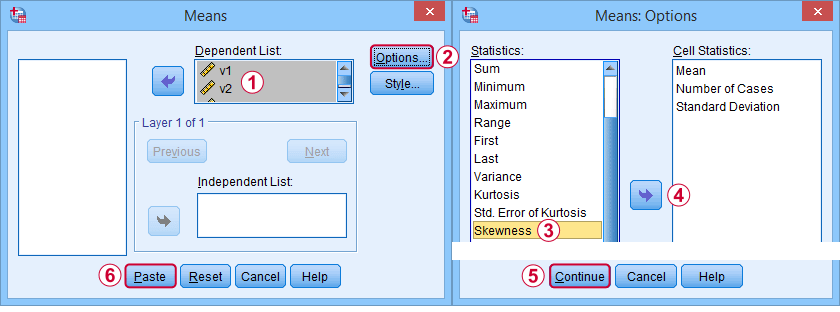
Syntaksen kan være så simpel sommeans v1 to v5
/cells skew.En meget komplet tabel -inklusive gennemsnit, standardafvigelser, medianer og mere- køres fraommeans v1 to v5
/cells count min max mean median stddev skew kurt.Resultatet er vist nedenfor.
Skewness – Implikationer for dataanalyse
Mange analyser -ANOVA, t-test, regression og andre- kræver normalitetsantagelsen: Variabler skal være normalfordelte i populationen. Den normale fordeling har en skævhed = 0. Så hvis man observerer en betydelig skævhed i nogle stikprøvedata, tyder det på, at normalitetsantagelsen er overtrådt.
Sådanne overtrædelser af normaliteten er ikke noget problem for store stikprøver – f.eks. N > 20 eller 25 eller deromkring. I dette tilfælde er de fleste test robuste over for sådanne overtrædelser. Dette skyldes det centrale grænseteorem. Kort sagt,for store stikprøvestørrelser er skævhed
ikke noget reelt problem for statistiske tests.Skævhed er dog ofte forbundet med store standardafvigelser. Disse kan resultere i store standardfejl og lav statistisk styrke. På samme måde kan en betydelig skævhed mindske chancen for at forkaste en nulhypotese for at påvise en effekt. I dette tilfælde kan en ikke-parametrisk test være et klogere valg, da den kan have større effekt.Overtrædelser af normaliteten udgør en reel trussel
for små stikprøvestørrelseraf -sige- N < 20 eller deromkring. Med små stikprøvestørrelser er mange test ikke robuste over for en overtrædelse af normalitetsantagelsen. Løsningen er – igen – at bruge en ikke-parametrisk test, fordi disse ikke kræver normalitet.
Sidst, men ikke mindst, findes der ikke nogen statistisk test til at undersøge, om populationens skævhed = 0. En indirekte måde at teste dette på er en normalitetstest som
- Kolmogorov-Smirnov-normalitetstest og
- Shapiro-Wilk-normalitetstest.
Men når der virkelig er behov for normalitet – med små stikprøvestørrelser – har sådanne test en lav effekt: de opnår måske ikke statistisk signifikans, selv når afvigelserne fra normaliteten er alvorlige. På den måde giver de dig primært en falsk følelse af sikkerhed.




