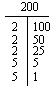Tal i deres primtal

admin 0 Comments Articles

Tal i deres primtal

Alle hele tal kan kategoriseres som enten primtal eller sammensatte tal, med undtagelse af nul og et, som er særtilfælde. Lad os tage et kig på forskellen mellem primtal og sammensatte tal. Primtal har præcis to faktorer, én og selve tallet. Hvis du kender dine delbarhedsregler (gennemgået i næste afsnit), er det en relativt nem opgave at bestemme primtalene fra 1-100. Her er primtalene op til 25:

2, 3, 5, 7, 11, 13, 17, 19, 23

Der er ikke noget mønster for at finde alle de primtal, der findes, selv om matematikere har fundet primtal med næsten otte millioner cifre. Dette er et af de resterende store matematiske mysterier derude for matematikere.

Sammensatte tal har mere end to faktorer, men ikke et uendeligt antal faktorer. Alle lige tal (undtagen tallet to) er sammensatte, da de alle kan deles med to.

Zero er hverken primtal eller sammensat. Da ethvert tal gange nul er lig med nul, er der et uendeligt antal faktorer for et produkt af nul. Et sammensat tal skal have et endeligt antal faktorer.

Et er heller ikke et primtal eller et sammensat tal. Den eneste måde at få et produkt af én på er ved at gange 1 x 1. Men dobbelte faktorer tælles kun én gang, så én har kun én faktor. (Et primtal har præcis to faktorer, så en kan ikke være primtal.)

Et typisk testspørgsmål vil bede dig om at finde ud af, hvilket tal fra en liste der er primtal (eller sammensat eller ingen af delene).

Prøv dette:

Spørgsmål

Hvilket af følgende er et primtal?

1. 33
2. 45
3. 41
4. 51
5. 51

Svaret

Det rigtige svar er C. 41 er et primtal; de andre tal er sammensatte. Vær forsigtig med 51 – det kommer fra 3 x 17.

Cool Rules

Divisionsregler er værktøjer, der hjælper dig med at lave mindre division. Delbarhedsreglerne kan hjælpe dig med at afgøre, om et tal er primtal eller sammensat, samt hjælpe dig med at opdele sammensatte tal i deres primfaktorer, hvilket er det emne, vi vil behandle næste gang.

Delbarhedsregler er genveje til at fortælle dig, om et tal er delbart med et andet tal. Reglerne dækker division ved tallene 2-10 og giver dig mulighed for at kontrollere tal op til 100. Klik på tallene i skemaet.

Spørgsmål

Hvilket af følgende tal er ikke delbart med 3?

1. 4.873
2. 7.521
3. 12.642
4. 25.308

Refalsk svar

Det rigtige svar er A. Den hurtige måde at løse denne opgave på er at bruge delbarhedsreglen; læg cifrene i hvert tal sammen og led efter det tal, der ikke er et multiplum af tre. Den langsomme måde ville være at lave hvert enkelt divisionsproblem – selv på en lommeregner vil denne metode tage længere tid!

Primfaktorisering: T’er og træer

Dette er endnu et emne, som du måske ikke har tænkt over siden mellemskolen. Den fundamentale sætning i aritmetik fastslår, at ethvert sammensat tal kan opdeles i et unikt produkt af primtal.

Primfaktorisering er den proces, der finder primtalsprodukterne af et givet sammensat tal. Primfaktorisering er nyttig i sig selv, men mange af dens anvendelser involverer brøker, som vi vil behandle senere.

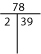
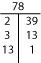
Du kan måske finde et tals primfaktorisering i dit hoved. For eksempel er 12 2 x 2 x 3 eller 22 x 3. (Primfaktoriseringer repræsenteres ofte med eksponenter.)

Hvis du ikke kan finde primfaktoriseringen mentalt, kan du prøve enten en faktor-T eller et faktortræ.

Faktor-T

I et Faktor-T har du to kolonner: den venstre kolonne med primtalene og den højre kolonne med gradvist mindre kvotienter fra division.

Stræk 1: Bestem et primtal, der dividerer med dit givne tal. Skriv dette tal i venstre kolonne.

Stræk 2: Skriv kvotienten af dit tal divideret med primtalstallet i højre kolonne.

Stræk 3: Søg nu efter et primtal, der dividerer med kvotienten, 39 i dette tilfælde. Fortsæt trin 1 og 2, indtil du har et tal i den højre kolonne. Tallene i venstre kolonne er din primfaktorisering! Primfaktoriseringen af 78 er 2 x 3 x 13. Intet andet tal har denne primfaktorisering.

Her er et andet eksempel på primfaktoriseringen af 200.

Primfaktoriseringen af 200 er 23 x 52.

Faktortræ

Med et faktortræ bryder du altid et tal op i produktet af to tal, indtil tallene er primtal. Der er mange taktikker for at komme i gang i toppen af træet, hvilket betyder, at træerne ikke nødvendigvis vil se ens ud, når de er lavet af forskellige personer. Brug det, der virker bedst for dig, til at finde ud af to tal, der kan multipliceres sammen til det tal, du har brug for.

Her er et andet eksempel på primfaktorisering af 200.

Review

• Primtal har præcis to faktorer, nemlig en og sig selv.
• Sammensatte tal har flere end to faktorer, men ikke et uendeligt antal.
• Nul og et er hverken primtal eller sammensatte tal.
• Delbarhedsregler er genveje, der kan hjælpe dig med at bestemme faktorer til et tal.
• Alle sammensatte tal kan skrives som et unikt produkt af primtal, hvilket kaldes et tals primfaktorisering.
• To praktiske metoder til at finde primfaktoriseringer er faktor-T’er og faktortræer.