To måder at dividere brøker på og nogle eksempler

admin 0 Comments Articles

To måder at dividere brøker på og nogle eksempler

I dette indlæg vil vi lære, hvordan man dividerer brøker. For at gøre dette skal vi se på to forskellige metoder:

Metode 1 til at dividere brøker: Denne metode består i at gange tælleren af den første brøk med nævneren af den anden brøk og derefter skrive svaret i den resulterende brøks tæller.

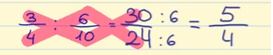
For eksempel for at dividere brøken

multiplicerer vi tælleren af den første brøk (3) med nævneren af den anden brøk (10). Dette giver os tælleren for den sidste brøk: 3 x 10 = 30.

Næst ganges nævneren af den første brøk (4) med tælleren af den anden brøk (6). Dette giver os nævneren for den endelige brøk: 4 x 6 = 24.

Det sidste trin er at forenkle brøken. Da begge tal er multipla af 6, kan vi dividere tælleren og nævneren med 6.

30 ÷ 6 = 5

24 ÷ 6 = 4

Dermed er resultatet af divisionen 5/4.

Metode 2 til at dividere brøker: Invertering og multiplikation

• Stræk 1: Inverter den anden brøk. Det vil sige, at vi bytter tælleren ud med nævneren.
• Stræk 2: Forenkl enhver tæller med en hvilken som helst nævner.
• Stræk 3: Multiplicer på tværs.

For eksempel skal vi dividere:

Stræk 1: Vi vender den anden brøk 6/4 om. Det bliver 4/6.

Stræk 2: Vi forenkler tællerne med nævnerne.

Tællerne er:
12 = 2 x 2 x 3
4 = 2 × 2

Nævnerne er:
5 = 5
6 = 2 × 3

Vi kan forenkle både fra tæller og nævner a 2 og a 3. Vi kalder denne proces for “krydsannullering”, hvis den ene tæller har en fælles faktor med den anden nævner.

Og vi multiplicerer på tværs:

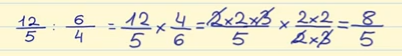
Vi håber, at du kunne lide dette indlæg.

Hvis du vil se flere eksempler, kan du besøge vores tidligere indlæg om ordopgaver med division af brøker og Sådan forenkler du brøker:

Hvis du vil lære meget mere matematik, så tilmeld dig på Smartick.

Lær mere:

• Lær og øv dig i at subtrahere eller addere brøker
• Lær og øv dig i at gange brøker
• Lær at dividere brøker med to forskellige metoder
• Lær at trække brøker fra hinanden
• Lær at subtrahere Brøker
• Øv dig i at addere brøker med eksempler

• Author
• Reneste indlæg

Content Creation Team.
Et tværfagligt og multikulturelt team bestående af matematikere, lærere, professorer og andre fagfolk inden for uddannelse!
De stræber efter at skabe det bedst mulige matematiske indhold.

Sidste indlæg af Smartick (se alle)

• Eksempler på matematiske ordproblemer i 3. klasse med løsninger – 25/03/2021
• Konsekvente indvendige vinkler: Hvad de er og hvordan man finder dem med eksempler – 03/11/2021
• Eksempler på ordproblemer i 2. klasse med løsninger – 02/04/2021