Einführung in die Wahrscheinlichkeitsrechnung: Artikel und Videos mit Lösungen!
 Würfeln, einen Parkplatz finden, beim Kartenspiel gewinnen; dies sind nur einige Situationen, in denen man die Wahrscheinlichkeit eines Ereignisses herausfinden möchte. Wenn Sie wissen wollen, wie man die Wahrscheinlichkeit ermittelt, müssen Sie zunächst herausfinden, welche Art von Frage Sie haben. Die Wahrscheinlichkeit, dass ein Ereignis eintritt, unterscheidet sich beispielsweise von der Wahrscheinlichkeit, dass sich die Mitglieder einer Gruppe für dieselbe Sache entscheiden.
Würfeln, einen Parkplatz finden, beim Kartenspiel gewinnen; dies sind nur einige Situationen, in denen man die Wahrscheinlichkeit eines Ereignisses herausfinden möchte. Wenn Sie wissen wollen, wie man die Wahrscheinlichkeit ermittelt, müssen Sie zunächst herausfinden, welche Art von Frage Sie haben. Die Wahrscheinlichkeit, dass ein Ereignis eintritt, unterscheidet sich beispielsweise von der Wahrscheinlichkeit, dass sich die Mitglieder einer Gruppe für dieselbe Sache entscheiden.
Einige Wahrscheinlichkeiten sind leicht zu ermitteln, wie z. B. die Wahrscheinlichkeit, einen Würfel zu werfen oder aus einem Kartenspiel auszuwählen.
Fragen, die den Binomischen Satz beinhalten, sind ebenfalls leicht zu erkennen. Bei diesen Arten von Experimenten sind die einzigen möglichen Ergebnisse eines Ereignisses „Erfolg“ oder „Misserfolg“: wie Ja/Nein, Kopf/Schwanz oder Schwarz/Weiß.
Andere Fragetypen, auf die du stoßen könntest, haben mit Menschen zu tun, z. B.:
- Auswahl einer Person aus einer Gruppe oder einem Komitee.
- Wahrscheinlichkeit, dass eine Gruppe das Gleiche wählt.
Ereignisse
Willst du die Wahrscheinlichkeit finden, dass ein einfaches Ereignis eintritt? Zum Beispiel, dass es regnet oder dass man in der Stadt einen Parkplatz findet? Siehe:
Wahrscheinlichkeit, dass ein einfaches Ereignis eintritt.
Wenn Sie hingegen das genaue Gegenteil wollen, siehe:
Wie man die Wahrscheinlichkeit herausfindet, dass ein Ereignis NICHT eintritt.
Geht es bei Ihrer Frage darum, dass ein Ereignis bei einem anderen Ereignis eintritt? Zum Beispiel die Wahrscheinlichkeit, einen Parkplatz zu finden, weil heute Spieltag ist, oder ein bestimmtes beliebtes Spielzeug am Black Friday zu finden? Wenn ja, dann schau nach:
- Wahrscheinlichkeit eines Ereignisses bei einem anderen Ereignis.
- Zwei Ereignisse, die zusammen auftreten.
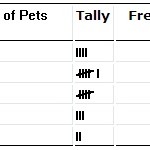
Eine Häufigkeitsverteilungstabelle.
Häufigkeitsverteilungen
Haben Sie eine Häufigkeitsverteilung, mit der Sie arbeiten können? Oder sind Sie in der Lage, eine Häufigkeitsverteilungstabelle mit Ihren gegebenen Daten zu erstellen? Zum Beispiel: Sie haben x Artikel mit bestimmten Merkmalen. Wahrscheinlichkeitshäufigkeitsverteilung.
Einführung in die Wahrscheinlichkeitsrechnung: Anleitungsartikel und Videos.
- Permutationen und Kombinationen: Wie man Probleme löst
- Wahrscheinlichkeitsprobleme: Lösen Sie sie auf einfache Weise!
- Wahrscheinlichkeit von a und b.
- Gesamtwahrscheinlichkeitsregel.
- Bayes Theorem Probleme: Einfache Lösungsschritte.
- Vorrangige Wahrscheinlichkeit (einschließlich uninformativ und konjugiert).
- Wie man eine Wahrscheinlichkeitsverteilung aus Daten erstellt.
- Wie man die Wahrscheinlichkeit der Auswahl einer Person aus einer Gruppe oder einem Ausschuss findet.
- Wie man die Wahrscheinlichkeit findet, dass ein Ereignis NICHT eintritt.
- Wahrscheinlichkeitshäufigkeitsverteilung.
- Wie man die Wahrscheinlichkeit findet, dass ein einfaches Ereignis eintritt.
- Zufälliges Ereignis: Wahrscheinlichkeit bei einem Prozentsatz.
- Wie man die Wahrscheinlichkeit findet, dass Gruppenmitglieder dasselbe wählen.
- Wie man die Wahrscheinlichkeit findet, dass zwei abhängige Ereignisse zusammen auftreten.
- Wie man die Wahrscheinlichkeit findet, dass ein Ereignis bei einem anderen Ereignis eintritt.
- Wie man einen Wahrscheinlichkeitsbaum (Entscheidungsbaum) verwendet, um Quoten zu berechnen.
- Wie man die Wahrscheinlichkeit des Ziehens einer Karte aus einem Stapel ermittelt.
- Wie man herausfindet, ob etwas ein sich gegenseitig ausschließendes Ereignis ist.
- Wie man den Unterschied zwischen abhängigen und unabhängigen Ereignissen erkennt.
- Wahrscheinlichkeit: Würfeln.
- Wie man ein Venn-Diagramm zeichnet.
- Wie man ein Euler-Diagramm erstellt.
- 5 wähle 3: Wie man Kombinationen löst.
- Wie man das fundamentale Zählprinzip anwendet.
- Wie man den Erwartungswert für eine diskrete Zufallsvariable findet.
Einführung in die Wahrscheinlichkeitsrechnung: Definitionen
- Axiomatische Wahrscheinlichkeitsrechnung.
- Benfordsches Gesetz
- Was ist ein Binomialversuch?
- Basisraten und der Basisratenfehler
- Brierwerte
- Kollektiv erschöpfend
- Was sind Kombinationen?
- Komplementäre Ereignisse.
- Bedingte Erwartung
- Was ist die bedingte relative Häufigkeit?
- Abzählbare Additivität
- Leere Menge
- Epistemische Wahrscheinlichkeit
- Ereignisräume.
- Was ist experimentelle Wahrscheinlichkeit?
- Gemeinsame Wahrscheinlichkeitsverteilungen.
- Grenzverteilung.
- Maximum-Likelihood-Schätzung
- Speicherlose Eigenschaft.
- Monte-Carlo-Methode.
- Monty-Hall-Problem
- Was ist ein sich gegenseitig ausschließendes Ereignis?
- Was ist ein sich gegenseitig einschließendes Ereignis?
- Gegenseitig unabhängig und paarweise unabhängig?
- Was ist die Multiplikationsregel?
- Nash-Gleichgewicht
- Nichtleere Menge
- Normale Wahrscheinlichkeits-Probleme.
- Was ist ein Normalwahrscheinlichkeitsdiagramm?
- Objektive Wahrscheinlichkeit
- Was ist das Odds Ratio?
- Prädiktive Analyse
- Was ist eine Wahrscheinlichkeitsverteilungstabelle?
- Wahrscheinlichkeitsmaß
- Was ist ein Wahrscheinlichkeitsraum?
- Wahrscheinlichkeitsvektoren
- Was sind Stichprobenräume?
- Stochastische Modelle.
- Was ist subjektive Wahrscheinlichkeit?
- Was ist theoretische Wahrscheinlichkeit?
- Was ist ein Urnenmodell?
Rechner.
- Online-Rechner für Permutationen und Kombinationen.
Wahrscheinlichkeitsformeln / Wahrscheinlichkeitsregeln
Eines der unangenehmsten Dinge, die Schüler an Formeln nicht mögen, ist das Fehlen von Formeln in der Wahrscheinlichkeitsrechnung und Statistik. Es gibt ein paar Grundregeln, darunter einige Notationen, die man kennen muss:
Wahrscheinlichkeitsbereich
0 ≤ P(A) ≤ 1
Dies besagt, dass die Wahrscheinlichkeit eines Ereignisses irgendwo zwischen Null und 100 % liegt (als Dezimalzahl ist das 0 und 1). Diese Regel sollten Sie sich merken, wenn Sie Wahrscheinlichkeiten von Ereignissen addieren oder multiplizieren. Wenn deine Antwort über 100 % liegt, ist das ein Hinweis darauf, dass du etwas falsch gemacht hast.
Regel der komplementären Ereignisse
P(AC) + P(A) = 1
Komplementäre Ereignisse treten auf, wenn es nur zwei Ergebnisse gibt, wie beim Werfen einer Münze. Einen Würfel zu werfen, um zu sehen, ob man eine Sechs erhält, ist ebenfalls ein komplementäres Ereignis; die einzigen beiden Ergebnisse sind, eine Sechs zu erhalten (1/6 Chance) oder keine Sechs zu erhalten (5/6 Chance). Die beiden Wahrscheinlichkeiten müssen sich zu 1 addieren.
Man kann diese Formel auch so schreiben:
p(A) + p(A‘) = 1
, was algebraisch umgestellt werden kann und dann lautet:
p(A‘) = 1 – p(A).
Alle drei Formeln sind äquivalent: Welche Terminologie (A‘ oder Ac) verwendet wird, bleibt dem Lehrbuchautor und dem Lehrer überlassen. Ich persönlich bevorzuge A‘, das ich „nicht A“ nenne. Die Wahrscheinlichkeit von „nicht A“ ist meiner Meinung nach leichter zu verstehen als „das Komplement“ (entweder ein Ereignis tritt ein, oder es tritt nicht ein).
Additionsregel
P(A∪B) = P(A) + P(B) – P(A∩B)
wobei ∪ die Vereinigung und ∩ die Schnittmenge ist.
Was dies (auf Englisch!), dass die Wahrscheinlichkeit, dass Ereignis A ODER Ereignis B (oder beide gleichzeitig) eintreten, wie folgt ist:
- Die Wahrscheinlichkeit, dass Ereignis A allein eintritt,
- Plus die Wahrscheinlichkeit, dass Ereignis B allein eintritt,
- Plus die Wahrscheinlichkeit, dass beide Ereignisse gleichzeitig eintreten.
Wenn man Ereignisse hat, die sich gegenseitig ausschließen, dann kann P(A∩B) nicht eintreten (die Ereignisse können nicht zusammen eintreten), also wird die Formel:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)
Disjunkte Ereignisse
Die Ereignisse A und B sind disjunkt, wenn:
P(A∩B) = 0
Das ist nur eine andere Art zu sagen, dass die Ereignisse sich gegenseitig ausschließen. Sie können nicht gleichzeitig eintreten.
Eine verwandte Formel ist P((A∪B)c) oder gleichbedeutend ((A∪B)‘). Im Englischen heißt das „not the union“. Um dies zu lösen, muss man die Vereinigung herausfinden und das Ergebnis von 1 abziehen (denn die Wahrscheinlichkeit, dass die Ereignisse eintreten oder nicht eintreten, muss sich zu 1 addieren).
Bedingte Wahrscheinlichkeit
P(A|B) = P(A∩B) / P(B)
Das Symbol „|“ bedeutet „unter der Voraussetzung, dass“. Mit anderen Worten: die Wahrscheinlichkeit, dass das Ereignis B eintritt, wenn das Ereignis A eintritt. Beispiele für die Verwendung der Formel finden Sie unter: Bedingte Wahrscheinlichkeit.
Bayes-Formel
P(A|B) = P(B|A) – P(A) / P(B)
Das Theorem von Bayes ist eine Möglichkeit, die bedingte Wahrscheinlichkeit zu berechnen, auch wenn es etwas differenzierter ist. Kurz gesagt, gibt es die tatsächliche Wahrscheinlichkeit eines Ereignisses an, wenn Informationen über Tests vorliegen. Zum Beispiel: Wie hoch ist die Wahrscheinlichkeit, dass Sie Krebs haben, wenn Ihr medizinischer Test positiv ist (Antwort = viel niedriger als Sie denken). Einige Beispiele finden Sie unter: Beispiele zum Bayes-Theorem und Posterior-Verteilungen / Posterior-Wahrscheinlichkeiten.
Unabhängige Ereignisse
Ereignisse A und B sind unabhängig, wenn das eine Ereignis keinen Einfluss auf die Wahrscheinlichkeit des anderen hat. Man sagt auch, dass Ereignisse unabhängig sind, wenn die folgende Gleichung gilt:
P(A∩B) = P(A) – P(B).
Diese Gleichung wird von der Multiplikationsregel abgeleitet, die besagt, dass P(A∩B) = P(A) * P(B|A). Da wir wissen, dass P(B|A) = P(B) für unabhängige Ereignisse ist, können wir P(B|A) durch P(B) ersetzen und erhalten so die Formel.
Einige Anmerkungen zu Wahrscheinlichkeitsregeln
In der Statistik geht es um Zufall und Schätzungen, nicht um absolute Werte und die „richtige Antwort“. Schauen Sie sich einfach eine Gallup-Umfrage an – sie sind selten mehr als 90 % sicher, dass sie die „richtige Antwort“ haben. Es gibt Techniken zur Ermittlung von Wahrscheinlichkeiten (z. B. das Multiplizieren oder Addieren zweier Wahrscheinlichkeiten). Abgesehen von der Binomialverteilungs-Tabelle und den obigen Formeln (die im wirklichen Leben nicht so oft verwendet werden) gibt es jedoch keine wirklichen Wahrscheinlichkeitsformeln, die man einfach anwenden kann. Du musst auf das alte Grundschulwissen zurückgreifen, die Logik (du erinnerst dich daran… sie war da, bevor sie anfingen, die Logik aus dir heraus zu testen).
Die drei Regeln der Wahrscheinlichkeitsformeln:
- Es gibt keine Regeln (naja, nur sehr wenige, außer den oben genannten).
- Verwendet Logik, keine Gleichungen.
- Es gibt viele, viele verschiedene Wege, um zur Antwort zu kommen – keiner davon verwendet wirklich Formeln.
Hier ist eine Frage, die heute Morgen in meinem Posteingang ankam und die sich mit Wahrscheinlichkeiten befasst:
„Wenn du versuchst, 6 Baseballkarten zu sammeln, die in Päckchen mit Käsebällchen verpackt sind, angenommen, sie sind gleichmäßig verteilt, wie viele Päckchen mit Käsebällchen müsstest du kaufen, bevor du alle 6 Karten hast?“
Schritt 1 zur Lösung dieses Problems ist die Erkenntnis, dass du die Antwort nicht in einer Tabelle nachschlagen kannst. Um die Aufgabe zu lösen, musst du wie ein Kind denken.
Karte Nr. 1:Du bist wieder 8 Jahre alt und gehst in einen Laden mit genug Geld, um eine Tüte Käsebällchen zu kaufen. Du hoffst, dass du alle 5 Baseballkarten sammeln kannst, aber du hast noch keine. Wie stehen die Chancen, dass du eine Tüte kaufst und eine Karte bekommst, die du haben willst?
Die Antwort ist natürlich 100%. Wenn du deine erste Tüte kaufst, hast du eine 100%ige Chance, dass eine Karte drin ist, die du haben willst.
Karte Nr. 2: Jetzt wird es ein bisschen kniffliger. Du kehrst in den Laden zurück, um Karte Nr. 2 zu holen. Aber da du bereits Karte Nr. 1, Mickey Mantle, bekommen hast. Du willst ihn nicht noch einmal, aber es besteht eine 1/5 Chance, dass du ihn bekommst (und damit eine 4/5 Chance, dass du ihn nicht bekommst). Wie viele Tüten Käsebällchen du kaufen musst, um Karte Nr. 2 zu bekommen, wird zu einem Verhältnisproblem. Du kannst es in deinem Kopf ausrechnen, aber wenn du es mathematisch modellieren willst, musst du die Gleichung aufstellen. Wenn du mit einer Tüte Käsebällchen eine 80%ige Chance hast, die gewünschte Karte zu bekommen, wie viele Tüten musst du dann kaufen, um eine 100%ige Chance zu bekommen?
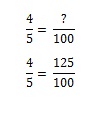
Um 100% zu bekommen, müsstest du 1,25 Tüten kaufen.
Karte Nr. 3:Die Chancen werden immer schlechter. Du hast eine 60%ige Chance, die dritte Baseballkarte zu bekommen, und du musst 1,667 Tüten kaufen, um diese dritte Karte zu bekommen.
Karte Nr. 4:Die Chancen werden langsam etwas schlechter. Du hast eine 40%ige Chance, die vierte Baseballkarte zu bekommen, und du musst 2,5 Tüten kaufen, um diese dritte Karte zu bekommen.
Karte Nr. 5:Die Chancen stehen gegen dich. Du hast eine 20%ige Chance, die letzte Karte zu bekommen, und du musst 5 Beutel kaufen, um diese dritte Karte zu bekommen.
Die Gesamtzahl der Beutel, die du kaufen musst, ist also gleich:
1 + 1,25 + 1,667 + 2,5 + 5
Aber warte! (Und hier kommt ein wenig Logik ins Spiel). Du kannst nicht in einen Laden gehen und 1,25 Tüten Käsebällchen kaufen, also musst du aufrunden. Die Gleichung lautet also:
1 + 2 + 2 + 3 + 5 = 13 Tüten.
Ein wichtiger Hinweis zu Formeln: Denken Sie daran, dass nichts absolut ist. Ich bin einigermaßen zuversichtlich, dass du, wenn du 13 Tüten Käsebällchen kaufst und davon ausgehst, dass die Karten gleichmäßig verteilt sind, alle 5 Karten bekommen würdest. Aber… bei der Wahrscheinlichkeit geht es um den Zufall, und es könnte sein, dass du einfach Pech hast, wenn du 10 Mal hintereinander dieselbe Karte bekommst (ich erinnere mich, dass mir das als Kind passiert ist). Es könnte aber auch eine andere Erklärung für Ihr „Pech“ geben, nämlich dass die Unternehmen wollen, dass Sie so viele Tüten wie möglich kaufen, und deshalb versuchen, die Chancen zu ihren Gunsten zu gestalten. Selbst wenn die Karten gleichmäßig verteilt sind, könnte das Unternehmen Tüten mit den Karten Nr. 1, Nr. 2 und Nr. 3 an eine Filiale schicken (und Sie so dazu bringen, mehr als die Hälfte der Karten zu sammeln) und Nr. 4 und Nr. 5 an eine andere Filiale.
Welche anderen Möglichkeiten fallen dir ein, mit denen die Hersteller die Chancen zu ihren Gunsten verändern könnten?
Wahrscheinlichkeit, dass eine Gruppe das Gleiche wählt
Wahrscheinlichkeitsfragen können in verschiedene Arten unterteilt werden. Bei der Frage nach der Wahrscheinlichkeit, dass eine Gruppe das Gleiche wählt, geht es um die Handlungen zufälliger Mitglieder einer Gruppe (die so klein sein kann wie ein Ausschuss oder so groß wie die Bevölkerung der USA).
Diese Wahrscheinlichkeitsfragen geben Ihnen eine Gruppe vor und bitten Sie, die Wahrscheinlichkeit zu berechnen, dass ein Ereignis für eine bestimmte Anzahl zufälliger Mitglieder dieser Gruppe eintritt.
Wahrscheinlichkeit einer Gruppe, die sich für dieselbe Sache entscheidet: Schritte
Beispielproblem: Auf einer Buchmesse befinden sich 200 Personen. 159 von ihnen werden mindestens ein Buch kaufen. Wenn man 5 zufällige Personen befragt, die aus der Tür kommen, wie groß ist die Wahrscheinlichkeit, dass sie alle mindestens ein Buch gekauft haben?

Wie groß ist die Wahrscheinlichkeit, dass eine Gruppe mindestens ein Buch kauft?
Schritt 1: Wandeln Sie die Daten in der Frage in einen Bruch um. Zum Beispiel kann der Satz „159 Personen von 200“ umgewandelt werden in: 159/200.
Schritt 2: Multiplizieren Sie den Bruch mit sich selbst. Wiederholen Sie diesen Vorgang für so viele zufällige Elemente (d. h. Personen), wie Sie auswählen. In unserem Beispiel haben wir 5 Personen befragt, also wollen wir:
159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
So findet man die Wahrscheinlichkeit, dass eine Gruppe das Gleiche wählt!
Tipp: Es kann einfacher sein, den Bruch vor dem Multiplizieren in eine Dezimalzahl umzuwandeln. In diesem Fall ist 159/200 = 0,795.
Sieh dir unseren YouTube-Kanal an, um mehr Hilfe und Tipps zur Statistik zu erhalten! Wir haben Videos für die häufigsten Probleme, auf die du wahrscheinlich stoßen wirst. Plus Videos zur Verwendung von Excel in der Statistik > von der Erstellung grundlegender Balkendiagramme bis zur Lösung komplexer Datenanalyseprobleme.
Stephanie Glen. „Einführung in die Wahrscheinlichkeitsrechnung: Artikel und Videos mit Lösungen!“ Von StatisticsHowTo.com: Elementare Statistik für den Rest von uns! https://www.statisticshowto.com/probability-and-statistics/probability-main-index/
——————————————————————————
Brauchen Sie Hilfe bei einer Hausaufgabe oder einer Prüfungsfrage? Mit Chegg Study können Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf dem Gebiet erhalten. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!




