Skewness – Kurze Einführung, Beispiele & Formeln
Skewness ist eine Zahl, die angibt, wie stark
eine Variable asymmetrisch verteilt ist.
- Beispiel für positive (rechte) Schiefe
- Beispiel für negative (linke) Schiefe
- Bevölkerungsschiefe – Formel und Berechnung
- Stichprobenschiefe – Formel und Berechnung
- Skewness in SPSS
- Skewness – Implikationen für die Datenanalyse
Positives (rechtes) Skewness-Beispiel
Ein Wissenschaftler lässt 1,000 Personen einige psychologische Tests absolvieren. Für Test 5 haben die Testergebnisse eine Schiefe = 2,0. Ein Histogramm dieser Werte ist unten dargestellt.
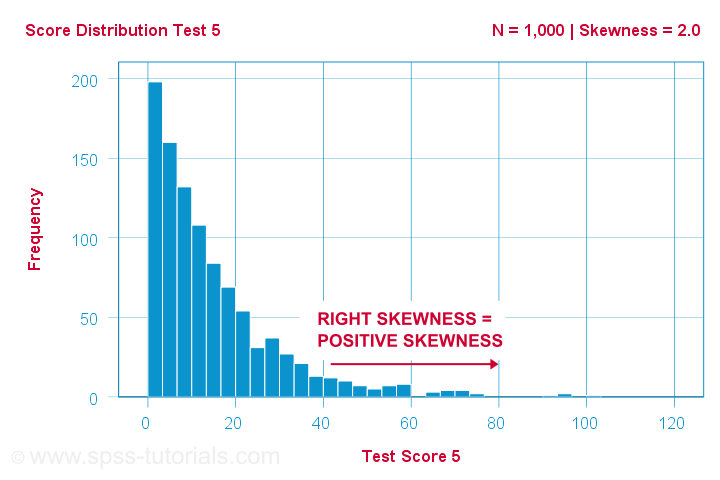
Das Histogramm zeigt eine sehr asymmetrische Häufigkeitsverteilung. Die meisten Personen erreichen 20 Punkte oder weniger, aber der rechte Schwanz reicht bis zu 90 oder so. Diese Verteilung ist rechtsschief.
Wenn wir uns auf der x-Achse nach rechts bewegen, gehen wir von 0 über 20 zu 40 Punkten und so weiter. Nach rechts im Diagramm werden die Werte also immer positiver. Daher ist die rechte Schiefe eine positive Schiefe, was bedeutet, dass die Schiefe > 0 ist. In diesem ersten Beispiel ist die Schiefe = 2,0, wie in der rechten oberen Ecke des Diagramms angegeben. Die Ergebnisse sind stark positiv schief.
Negative (linke) Schiefe Beispiel
Eine andere Variable – die Ergebnisse von Test 2 – haben eine Schiefe von = -1,0. Ihr Histogramm ist unten dargestellt.

Der Großteil der Ergebnisse liegt zwischen 60 und 100 oder so. Der linke Schwanz ist jedoch etwas gestreckt. Diese Verteilung ist also linksschief.
Rechts: nach links, nach links. Wenn wir die x-Achse nach links verfolgen, bewegen wir uns auf negativere Werte zu. Deshalb ist die linke Schiefe eine negative Schiefe, und tatsächlich ist die Schiefe = -1,0 für diese Werte. Ihre Verteilung ist linksschief. Sie ist jedoch weniger schief – oder symmetrischer – als unser erstes Beispiel, das eine Schiefe von 2,0 hatte.
Symmetrische Verteilungen implizieren eine Schiefe von Null
Schließlich haben symmetrische Verteilungen eine Schiefe von 0. Die Ergebnisse von Test 3 – mit einer Schiefe von 0,1 – kommen dem sehr nahe.

Nun sind die beobachteten Verteilungen selten genau symmetrisch. Dies ist vor allem bei einigen theoretischen Stichprobenverteilungen der Fall. Einige Beispiele sind
- die (Standard-)Normalverteilung;
- die t-Verteilung und
- die Binomialverteilung, wenn p = 0,5 ist.
Diese Verteilungen sind alle genau symmetrisch und haben somit eine Schiefe = 0.000…
Bevölkerungsschiefe – Formel und Berechnung
Wenn Sie die Schiefe für eine oder mehrere Variablen berechnen möchten, überlassen Sie die Berechnungen einfach einer Software. Aber – nur der Vollständigkeit halber – führe ich die Formeln trotzdem auf.
Wenn deine Daten die gesamte Bevölkerung enthalten, berechne die Schiefe der Bevölkerung wie folgt:
$$Population\;Schiefe = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$$
wobei
- \(X_i\) jeder einzelne Wert ist;
- \(\mu\) ist der Mittelwert der Population;
- \(\sigma\) ist die Standardabweichung der Population und
- \(N\) ist die Populationsgröße.
Ein Berechnungsbeispiel mit dieser Formel finden Sie in diesem Googlesheet (siehe unten).
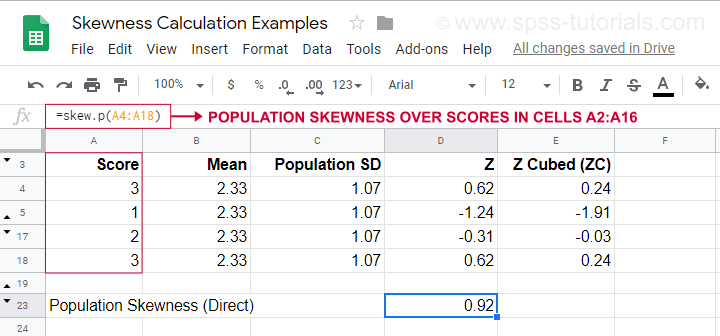
Es zeigt auch, wie man die Populationsschiefe direkt mit=SKEW.P(…)erhält, wobei „.P“ für „Population“ steht. Dies bestätigt das Ergebnis unserer manuellen Berechnung. Leider berechnen weder SPSS noch JASP die Populationsschiefe: beide sind auf die Stichprobenschiefe beschränkt.
Stichprobenschiefe – Formel und Berechnung
Wenn Ihre Daten eine einfache Zufallsstichprobe aus einer Population enthalten, verwenden Sie
$$Stichprobe\;Schiefe = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$
wobei
- \(X_i\) jeder einzelne Wert ist;
- \(\overline{X}\) ist der Stichprobenmittelwert;
- \(S\) ist die Stichprobenstandardabweichung und
- \(N\) ist der Stichprobenumfang.
Eine Beispielrechnung ist in diesem Googlesheet (siehe unten) dargestellt.
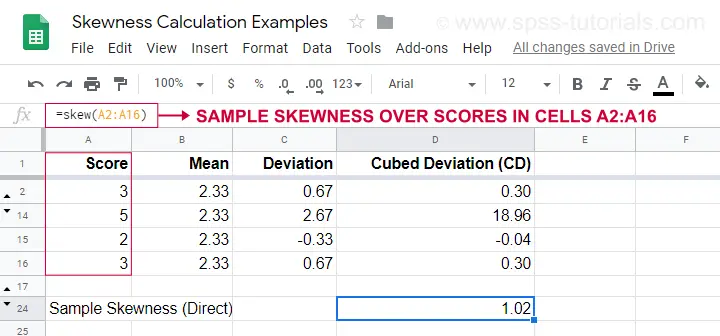
Eine einfachere Möglichkeit, die Stichprobenschiefe zu erhalten, ist die Verwendung von=SKEW(…).was das Ergebnis unserer manuellen Berechnung bestätigt.
Schiefe in SPSS
Zunächst einmal bezieht sich „Schiefe“ in SPSS immer auf die Stichprobenschiefe: Es wird stillschweigend davon ausgegangen, dass Ihre Daten eine Stichprobe und nicht die gesamte Population enthalten. Es gibt viele Optionen, um sie zu erhalten. Mein Favorit ist MEANS, weil die Syntax und die Ausgabe sauber und einfach sind. Die nachstehenden Screenshots führen Sie durch das Programm.

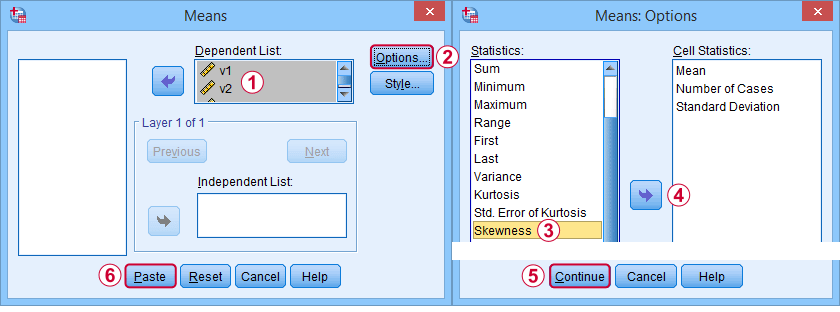
Die Syntax kann so einfach sein wiemeans v1 to v5
/cells skew.Eine sehr vollständige Tabelle – einschließlich Mittelwerten, Standardabweichungen, Medianen und mehr – wird vonmeans v1 to v5
/cells count min max mean median stddev skew kurt ausgeführt.Das Ergebnis ist unten dargestellt.
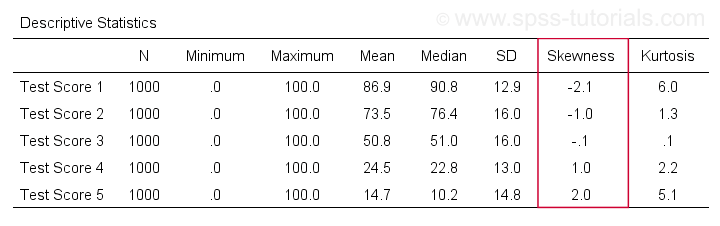
Skewness – Implikationen für die Datenanalyse
Viele Analysen -ANOVA, t-Tests, Regression und andere – erfordern die Normalitätsannahme: Variablen sollten in der Population normalverteilt sein. Die Normalverteilung hat eine Schiefe = 0. Die Beobachtung einer beträchtlichen Schiefe in einigen Stichprobendaten deutet also darauf hin, dass die Normalitätsannahme verletzt ist.
Solche Verletzungen der Normalität sind kein Problem für große Stichprobenumfänge – sagen wir N > 20 oder 25 oder so. In diesem Fall sind die meisten Tests robust gegenüber solchen Verstößen. Dies ist auf den zentralen Grenzwertsatz zurückzuführen. Kurz gesagt, bei großen Stichprobenumfängen ist Schiefe kein wirkliches Problem für statistische Tests, aber Schiefe ist oft mit großen Standardabweichungen verbunden. Diese können zu großen Standardfehlern und geringer statistischer Aussagekraft führen. So kann eine erhebliche Schiefe die Wahrscheinlichkeit verringern, eine Nullhypothese abzulehnen, um eine Wirkung nachzuweisen. In diesem Fall kann ein nichtparametrischer Test die bessere Wahl sein, da er eine höhere Aussagekraft hat.9391>Verletzungen der Normalität stellen eine echte Bedrohung für kleine Stichprobengrößen von – sagen wir – N < 20 oder so dar. Bei kleinen Stichprobengrößen sind viele Tests nicht robust gegenüber einer Verletzung der Normalitätsannahme. Die Lösung ist -wieder einmal- die Verwendung eines nichtparametrischen Tests, da dieser keine Normalität voraussetzt.
Zu guter Letzt gibt es keinen statistischen Test, um zu prüfen, ob die Schiefe der Bevölkerung = 0 ist. Eine indirekte Möglichkeit, dies zu prüfen, ist ein Normalitätstest wie
- der Kolmogorov-Smirnov-Normalitätstest und
- der Shapiro-Wilk-Normalitätstest.
Wenn jedoch Normalität wirklich benötigt wird – bei kleinen Stichprobengrößen – haben solche Tests eine geringe Aussagekraft: Sie erreichen möglicherweise keine statistische Signifikanz, selbst wenn die Abweichungen von der Normalität schwerwiegend sind. So vermitteln sie hauptsächlich ein falsches Gefühl der Sicherheit.




