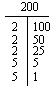Zahlen in ihrer Primzahl
Alle ganzen Zahlen werden entweder als Primzahlen oder als zusammengesetzte Zahlen kategorisiert, mit Ausnahme von Null und Eins, die Sonderfälle sind. Schauen wir uns den Unterschied zwischen Primzahlen und zusammengesetzten Zahlen an. Primzahlen haben genau zwei Faktoren, nämlich einen und die Zahl selbst. Wenn Sie die Teilbarkeitsregeln kennen (die im nächsten Abschnitt behandelt werden), ist die Bestimmung der Primzahlen von 1-100 eine relativ einfache Aufgabe. Hier sind die Primzahlen bis 25:
2, 3, 5, 7, 11, 13, 17, 19, 23
Es gibt kein Muster, um alle Primzahlen zu finden, die es gibt, obwohl Mathematiker Primzahlen mit fast acht Millionen Stellen gefunden haben. Dies ist eines der verbleibenden großen mathematischen Rätsel für Mathematiker.
Zusammengesetzte Zahlen haben mehr als zwei Faktoren, aber keine unendliche Anzahl von Faktoren. Alle geraden Zahlen (außer der Zahl zwei) sind zusammengesetzt, da sie alle durch zwei teilbar sind.
Die Null ist weder prim noch zusammengesetzt. Da jede Zahl mal Null gleich Null ist, gibt es unendlich viele Faktoren für ein Produkt von Null. Eine zusammengesetzte Zahl muss eine endliche Anzahl von Faktoren haben.
Eine ist ebenfalls weder prim noch zusammengesetzt. Die einzige Möglichkeit, ein Produkt von Eins zu erhalten, ist die Multiplikation von 1 x 1. Aber doppelte Faktoren werden nur einmal gezählt, also hat Eins nur einen Faktor. (Eine Primzahl hat genau zwei Faktoren, also kann Eins keine Primzahl sein.)
Eine typische Testfrage verlangt, dass du herausfindest, welche Zahl aus einer Liste eine Primzahl (oder eine zusammengesetzte Zahl oder keine von beiden) ist.
Versuch es hiermit:
Frage
Welche der folgenden Zahlen ist eine Primzahl?
- 33
- 45
- 41
- 51
Antwort aufdecken
Die richtige Antwort ist C. Einundvierzig ist eine Primzahl; die anderen Zahlen sind zusammengesetzt. Sei vorsichtig mit 51 – es kommt von 3 x 17.
Cool Rules
Die Teilbarkeitsregeln sind Hilfsmittel, die dir helfen, weniger Divisionen durchzuführen. Die Teilbarkeitsregeln können dir dabei helfen, festzustellen, ob eine Zahl primär oder zusammengesetzt ist, und sie helfen dir auch, zusammengesetzte Zahlen in ihre Primfaktoren zu zerlegen, das Thema, das wir als Nächstes behandeln werden.
Die Teilbarkeitsregeln sind Abkürzungen, die dir sagen, ob eine Zahl durch eine andere teilbar ist. Die Regeln decken die Division durch die Zahlen 2-10 ab und ermöglichen es dir, Zahlen bis 100 zu überprüfen. Klicken Sie auf die Zahlen in der Tabelle.
| Teilbarkeitsregeln | ||
|---|---|---|
| 2 | 3 | 4 |
| 5 | 6 | 7 |
| 8 | 9 | 10 |
Frage
Welche der folgenden Zahlen ist nicht durch 3 teilbar?
- 4.873
- 7.521
- 12.642
- 25.308
Antwort aufdecken
Die richtige Antwort ist A. Der schnelle Weg, dieses Problem zu lösen, ist, die Teilbarkeitsregel zu verwenden; addiere die Ziffern jeder Zahl und suche diejenige, die kein Vielfaches von drei ist. Der langsame Weg wäre, jedes Divisionsproblem zu lösen – selbst auf einem Taschenrechner dauert diese Methode länger!
Prime Faktorisierung: T’s and Tree
Dies ist ein weiteres Thema, an das du vielleicht seit der Mittelschule nicht mehr gedacht hast. Der Fundamentalsatz der Arithmetik besagt, dass jede zusammengesetzte Zahl in ein eindeutiges Produkt von Primzahlen zerlegt werden kann.
Die Primfaktorzerlegung ist der Prozess, der die Primzahlprodukte einer gegebenen zusammengesetzten Zahl findet. Die Primfaktorzerlegung ist an sich nützlich, aber viele ihrer Anwendungen haben mit Brüchen zu tun, die wir weiter unten behandeln werden.
Du kannst die Primfaktorzerlegung einer Zahl vielleicht im Kopf finden. Zum Beispiel ist 12 2 x 2 x 3 oder 22 x 3. (Primfaktorzerlegungen werden oft mit Exponenten dargestellt.)
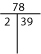
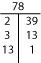
Wenn du die Primfaktorzerlegung nicht im Kopf finden kannst, versuche es mit einem Faktor-T oder einem Faktorenbaum.
Rückblick
- Primzahlen haben genau zwei Faktoren, nämlich eins und sich selbst.
- Zusammengesetzte Zahlen haben mehr als zwei Faktoren, aber nicht unendlich viele.
- Null und eins sind weder prim noch zusammengesetzt.
- Teilbarkeitsregeln sind Abkürzungen, die bei der Bestimmung der Faktoren einer Zahl helfen können.
- Jede zusammengesetzte Zahl kann als eindeutiges Produkt von Primzahlen geschrieben werden, was als Primfaktorzerlegung einer Zahl bezeichnet wird.
- Zwei praktische Methoden, um Primfaktorzerlegungen zu finden, sind Faktor-T’s und Faktorenbäume.