Eigenschappen van vierhoeken – Rechthoek, Vierkant, Parallelogram, Rhombus, Trapezium
In de euclidische meetkunde is een vierhoek een vierzijdige 2D-figuur waarvan de som van de inwendige hoeken 360° is. Het woord vierzijdig is afgeleid van twee Latijnse woorden “quadri” en “latus”, die respectievelijk vier en zijde betekenen. Daarom is het identificeren van de eigenschappen van vierhoeken belangrijk wanneer men ze probeert te onderscheiden van andere veelhoeken.
Dus, wat zijn de eigenschappen van vierhoeken? Er zijn twee eigenschappen van vierhoeken:
- Een vierhoek moet een gesloten vorm met 4 zijden zijn
- Alle inwendige hoeken van een vierhoek zijn samen 360°
In dit artikel krijgt u een idee over de 5 soorten vierhoeken en leert u de eigenschappen van vierhoeken kennen.
Dit is wat je in het artikel zult lezen:
- Verschillende soorten vierhoeken
- Rechthoek
- Eigenschappen van rechthoeken
- Rechthoekformules
- Vierkant
- Eigenschappen van een vierkant
- Vormen van vierkanten
- Parallellogram
- Eigenschappen van parallellogrammen
- Parallellogramformules
- Ruit
- Eigenschappen van een ruit
- Ruit formules
- Trapezium/Trapezium
- Eigenschappen van een Trapezium
- Trapezium formules
- Eigenschappen van vierhoeken
- Belangrijke formules van vierhoeken
- Vragen over vierhoeken
Hier een video waarin de eigenschappen van vierhoeken worden uitgelegd:
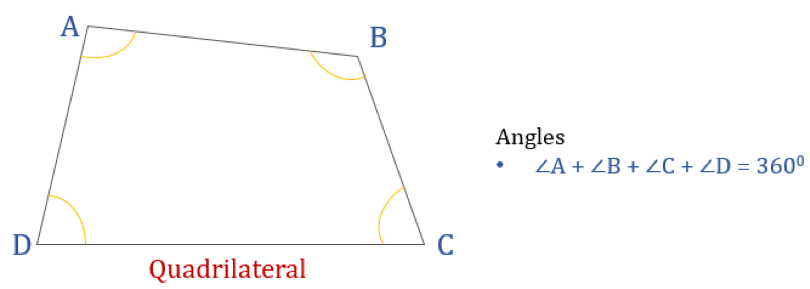
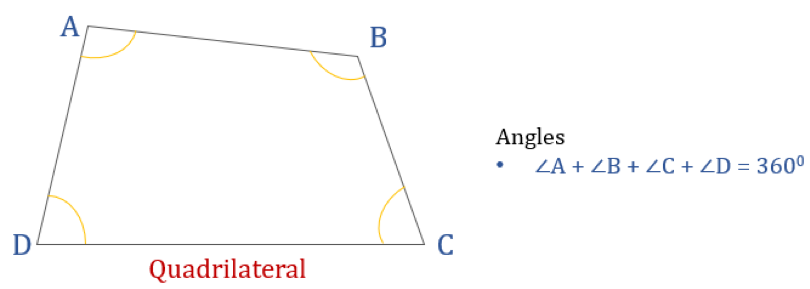
Het diagram hieronder toont een vierhoek ABCD en de som van zijn inwendige hoeken. De som van alle binnenhoeken is 360°.
Dus ∠A + ∠B + ∠C + ∠D = 360°
Verschillende soorten vierhoeken
Er zijn 5 soorten vierhoeken op basis van hun vorm. Deze 5 vierhoeken zijn:
- Rechthoek
- Vierkant
- Parallelogram
- Ruit
- Trapezium
Laten we elk van deze 5 vierhoeken eens in detail bespreken:
Hier volgen vragen die je zullen leren hoe je de eigenschappen van alle 5 de vierhoeken die je in dit artikel zult leren, kunt toepassen.
Rechthoek
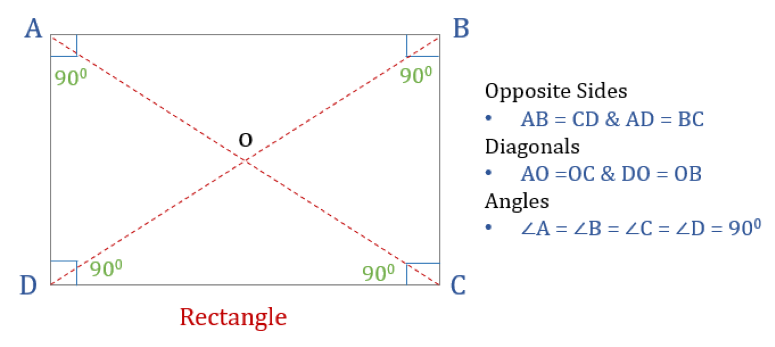
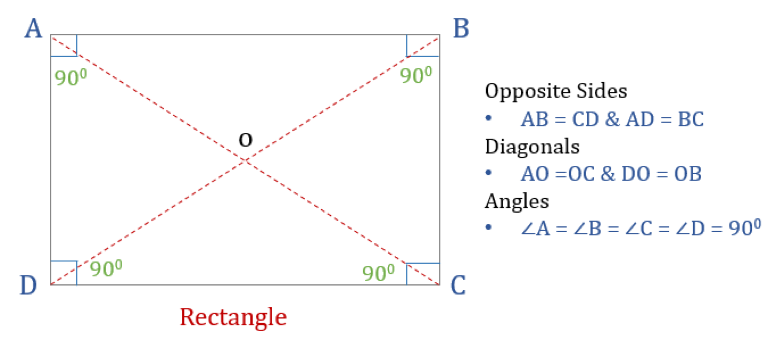
Een rechthoek is een vierhoek met vier rechte hoeken. Alle hoeken in een rechthoek zijn dus gelijk (360°/4 = 90°). Bovendien zijn de tegenover elkaar liggende zijden van een rechthoek evenwijdig en gelijk, en snijden diagonalen elkaar in tweeën.
Eigenschappen van rechthoeken
Een rechthoek heeft drie eigenschappen:
- Alle hoeken van een rechthoek zijn 90°
- Opposite zijden van een rechthoek zijn gelijk en Parallel
- Diagonalen van een rechthoek snijden elkaar
Rechthoekformule – Oppervlakte en omtrek van een rechthoek
Als de lengte van de rechthoek L is en de breedte B dan,
- Oppervlakte van een rechthoek = Lengte × breedte of L × B
- Oppervlakte van een rechthoek = 2 × (L + B)
Deze oefenvragen helpen je de eigenschappen van rechthoeken
Vierkant
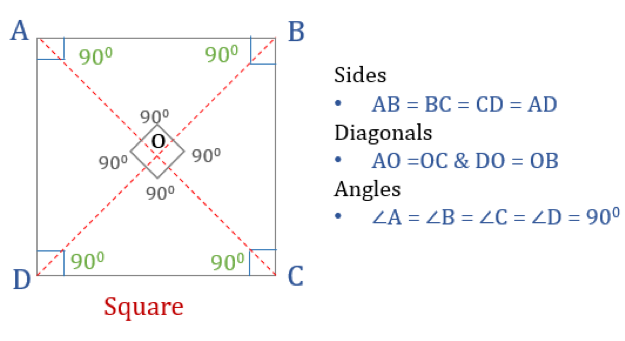
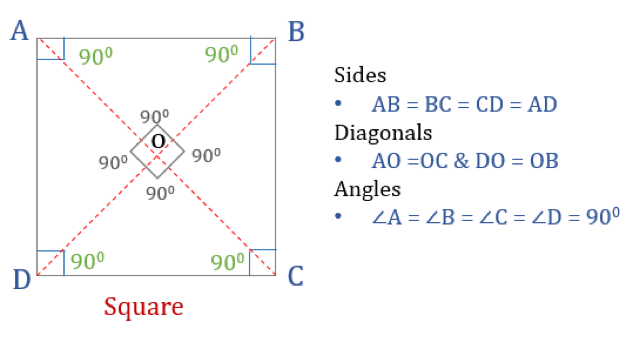
Het vierkant is een vierhoek met vier gelijke zijden en hoeken. Het is ook een regelmatige vierhoek omdat zowel de zijden als de hoeken gelijk zijn. Net als een rechthoek heeft een vierkant vier hoeken van elk 90°. Het kan ook gezien worden als een rechthoek waarvan de twee aangrenzende zijden gelijk zijn.
Eigenschappen van een vierkant
Om een vierhoek een vierkant te laten zijn, moet het bepaalde eigenschappen bezitten. Hier zijn de drie eigenschappen van vierkanten:
- Alle hoeken van een vierkant zijn 90°
- Alle zijden van een vierkant zijn gelijk en evenwijdig aan elkaar
- Diagonalen snijden elkaar loodrecht
Vierkantformule – Oppervlakte en omtrek van een vierkant
Als de zijde van een vierkant ‘a’ is, dan,
- Bereik van het vierkant = a × a = a²
- Omtrek van het vierkant = 2 × (a + a) = 4a
Deze oefenvragen helpen je de eigenschappen van vierkanten
Het scoren van een Q50-51 op de GMAT helpt je een 700+ GMAT score te halen. Waarom begin je niet met je voorbereiding op de GMAT met onze gratis voorbereidingsmateriaal en begin je reis om een Q50-51 te halen op de GMAT. Leer van Carrie Law die in 3 weken van Q35 naar Q50 verbeterde.
Parallelogram
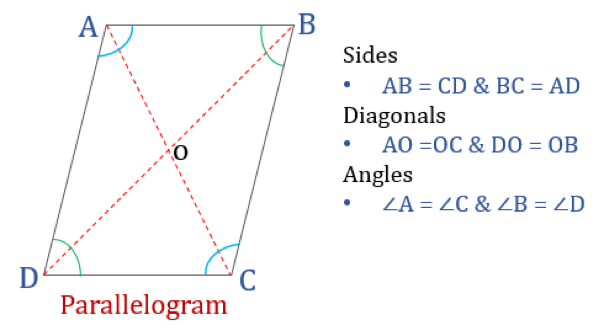
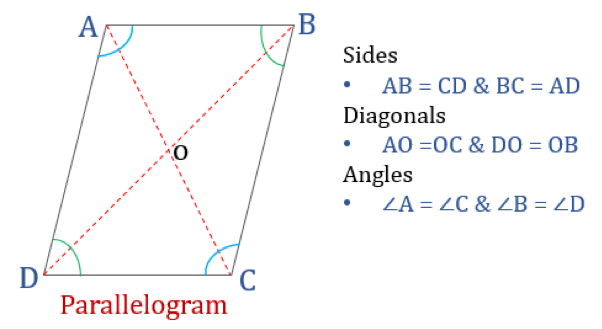
Een parallellogram is, zoals de naam al zegt, een eenvoudige vierhoek waarvan de tegenoverliggende zijden evenwijdig zijn. Het heeft dus twee paar evenwijdige zijden. Bovendien zijn de overstaande hoeken in een parallellogram gelijk en snijden de diagonalen elkaar.
Eigenschappen van een parallellogram
Een vierhoek die aan de onderstaande eigenschappen voldoet, wordt geclassificeerd als een parallellogram. Een parallellogram heeft vier eigenschappen:
- Opposite hoeken zijn gelijk
- Opposite zijden zijn gelijk en evenwijdig
- Diagonalen snijden elkaar
- Som van twee willekeurige aanliggende hoeken is 180°
Parallelogramformules – Oppervlakte en omtrek van een parallellogram
Als de lengte van een parallellogram ‘l’ is, de breedte is ‘b’ en de hoogte is ‘h’ dan:
- Omtrek van parallellogram= 2 × (l + b)
- Oppervlakte van het parallellogram = l × h
Deze oefenvragen helpen je bij het hard maken de eigenschappen van parallellogram
Rhombus
Een rhombus is een vierhoek waarvan alle vier de zijden even lang zijn en de tegenover elkaar liggende zijden evenwijdig aan elkaar zijn. De hoeken zijn echter niet gelijk aan 90°. Een ruit met rechte hoeken zou een vierkant worden. Een andere naam voor een ruit is “ruit”, omdat hij lijkt op de ruit in speelkaarten.
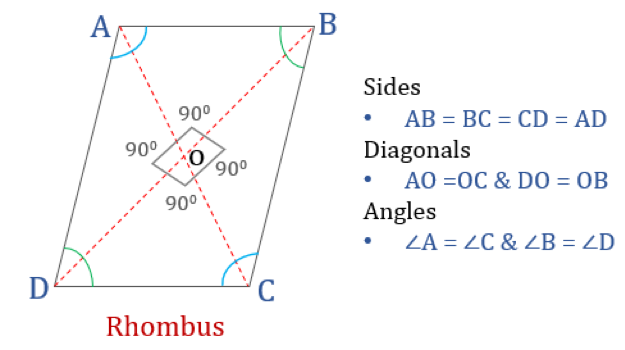
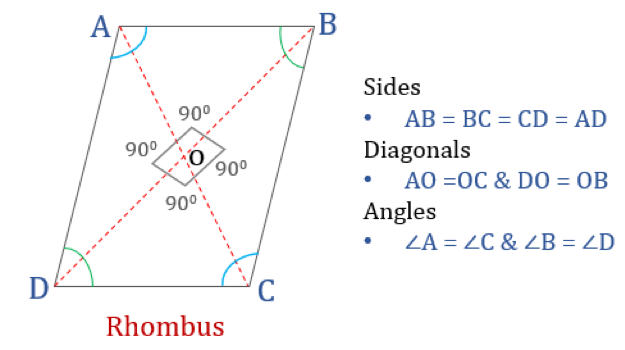
Eigenschappen van een ruit
Een ruit is een vierhoek die de volgende vier eigenschappen heeft:
- Opposiete hoeken zijn gelijk
- Alle zijden zijn gelijk en, tegengestelde zijden zijn evenwijdig
- Diagonalen snijden elkaar loodrecht
- Som van twee willekeurige aanliggende hoeken is 180°
Ruitformules – Oppervlakte en omtrek van een ruit
Als de zijde van een ruit a is dan, omtrek van een ruit = 4a
Als de lengte van twee diagonalen van de ruit d1 en d2 is, dan is de oppervlakte van een ruit = ½ × d1 × d2
Deze oefenvragen zullen helpen je de eigenschappen van ruit
Trapezium
Een trapezium (in de VS Trapezoïde genoemd) is een vierhoek die slechts één paar evenwijdige zijden heeft. De evenwijdige zijden worden “basis” genoemd en de andere twee zijden worden “benen” of laterale zijden genoemd.
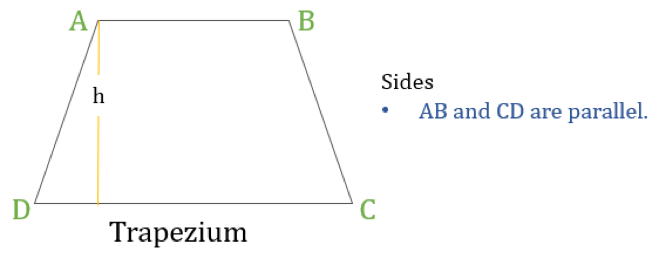
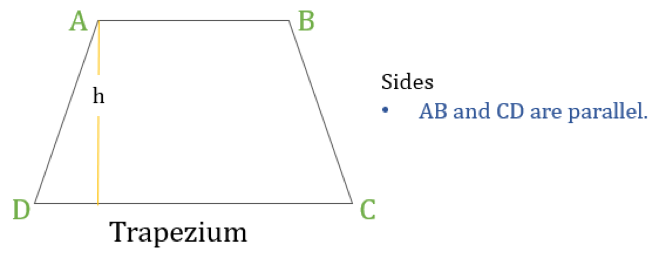
Eigenschappen van een trapezium
Een trapezium is een vierhoek waarvan de volgende eigenschap:
- Niet meer dan één paar tegenover elkaar liggende zijden zijn evenwijdig aan elkaar
Trapeziumformules – Oppervlakte en omtrek van een trapezium
Als de hoogte van een trapezium ‘h’ is (zoals in bovenstaand diagram) dan:
- Omtrek van het trapezium= Som van de lengten van alle zijden = AB + BC + CD + DA
- Oppervlakte van het trapezium = ½ × (Som van de lengten van de evenwijdige zijden) × h = ½ × (AB + CD) × h
Deze oefenvragen zullen je helpen om de eigenschappen van trapezium
Eigenschappen van vierhoeken
De onderstaande tabel vat alle eigenschappen van de vierhoeken samen die we tot nu toe hebben geleerd:
| Eigenschappen van vierhoeken | Rechthoek | Vierkant | Parallelogram | Rhombus | Trapezium |
| Alle zijden zijn gelijk | ✖ | ✔ | ✖ | ✔ | ✖ |
| Oppositiet Zijkanten zijn gelijk | ✔ | ✔ | ✔ | ✖ | |
| Opposite Zijkanten zijn evenwijdig | ✔ | ✔ | ✔ | ✔ | |
| Alle hoeken zijn gelijk | ✔ | ✖ | ✖ | ✖ | |
| Opposite angles are equal | ✔ | ✔ | ✔ | ✔ | ✖ |
| Som van twee aanliggende hoeken is 180 | ✔ | ✔ | ✔ | ✔ | ✖ |
| Bisecteren elkaar | ✔ | ✔ | ✔ | ✖ | |
| Bisecteren elkaar loodrecht | ✖ | ✔ | ✖ | ✖ |
In de onderstaande afbeelding worden ook de eigenschappen van vierhoeken samengevat:
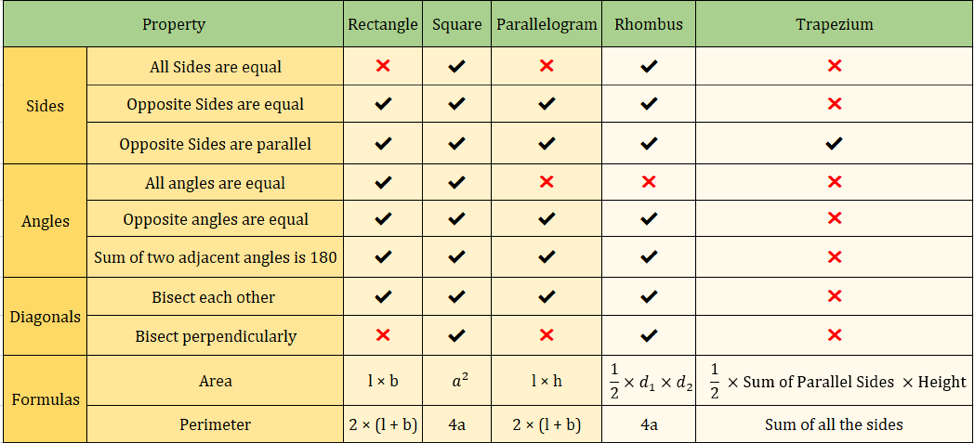
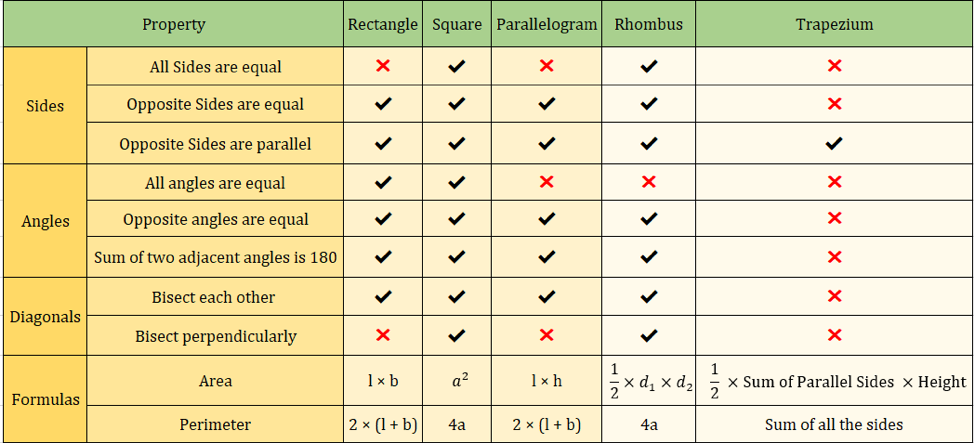
Belangrijke vierhoeksformules
De onderstaande tabel vat de formules over oppervlakte en omtrek van verschillende soorten vierhoeken samen:
| Vierzijdige formules | Rechthoek | Vierkant | Parallelogram | Ruit | Trapezium |
| Area | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Som van de evenwijdige zijden) × hoogte |
| Perimeter | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Som van alle zijden |
Verder lezen:
- Eigenschappen van Cirkel | Cirkelformules – Oppervlakte en omtrek
- Eigenschappen van Getallen – Even & Oneven | Priemgetal | HCF & LCM
- Eigenschappen van Driehoeken – Definitie | Soorten | Indeling
- Eigenschappen van Driehoeken – Definitie | Soorten | Classificatie
- Lijnen en hoeken – Eigenschappen en hun toepassing
Vierzijdige vragen
Laten we de toepassing van eigenschappen van vierhoeken oefenen op de volgende voorbeeldvragen:
Vraag 1
Adam wil een schutting bouwen om zijn rechthoekige tuin van lengte 10 meter en breedte 15 meter. Hoeveel meter schutting moet hij kopen om de hele tuin te omheinen?
- 20 meter
- 25 meter
- 30 meter
- 40 meter
- 50 meter
Oplossing
Stap 1: Gegeven
- Adam heeft een rechthoekige tuin.
- Hij heeft een lengte van 10 meter en een breedte van 15 meter.
- Hij wil er een schutting omheen bouwen.
Stap 2:
- De lengte vinden die nodig is om de schutting om de hele tuin heen te bouwen.
Stap 3: Benaderen en uitwerken
De schutting kan alleen om de buitenzijden van de tuin gebouwd worden.
- Dus de totale lengte van de benodigde schutting= Som van de lengtes van alle zijden van de tuin.
- Omdat de tuin rechthoekig is, is de som van de lengtes van alle zijden niets anders dan de omtrek van de tuin.
- Omtrek = 2 × (10 + 15) = 50 meter
Hieruit volgt dat de benodigde lengte van de schutting 50 meter is.
Daarom is optie E het juiste antwoord.
Vraag: 2
Steve wil één rechthoekige muur van zijn kamer verven. De kosten om de muur te schilderen bedragen $1,5 per vierkante meter. Als de muur 25 meter lang en 18 meter breed is, wat zijn dan de totale kosten om de muur te verven?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Oplossing
Stap 1: Gegeven
- Steve wil één muur van zijn kamer verven.
- De muur is 25 meter lang en 18 meter breed.
- De kosten om de muur te schilderen bedragen $1,5 per vierkante meter.
Stap 2: vinden
- De totale kosten om de muur te schilderen.
Stap 3: benaderen en uitwerken
- Een muur wordt over de hele oppervlakte geschilderd.
- Wanneer we dus de totale oppervlakte van de muur in vierkante meter vinden en die vermenigvuldigen met de kosten om 1 vierkante meter van de muur te schilderen, dan kunnen we de totale kosten.
- Oppervlakte van de muur = lengte × breedte = 25 meter × 18 meter = 450 vierkante meter
- Totale kosten om de muur te schilderen = 450 × $1.5 = $675
Hieruit volgt dat het juiste antwoord optie E is.
We hopen dat je nu de verschillende soorten vierhoeken, hun eigenschappen en formules hebt geleerd en hoe je deze concepten kunt toepassen om vragen over vierhoeken op te lossen. De toepassing van vierhoeken is belangrijk om geometrie vragen op de GMAT op te lossen. Als je van plan bent de GMAT te halen, kunnen wij je helpen met hoogwaardig studiemateriaal waar je gratis toegang tot hebt door je hier te registreren.
Hier zijn nog een paar artikelen over wiskunde:
- Verbeter de nauwkeurigheid in wiskunde vragen over veelhoeken
- Geometrie Vragen – Meest voorkomende fouten | GMAT Quant Prep
Als je van plan bent om de GMAT te doen, kunnen wij je toegang geven tot kwalitatief hoogstaande online content om je voor te bereiden. Wij zijn de meest beoordeelde GMAT prep bedrijf op gmatclub met meer dan 1950 beoordelingen.
Waarom neem je niet een gratis proefversie en oordeel zelf?
Schrijf ons op [email protected] in het geval van een query.




