Interpretar los coeficientes de la regresión lineal

Hoy en día existe una plétora de algoritmos de aprendizaje automático que podemos probar para encontrar el que mejor se adapte a nuestro problema particular. Algunos de los algoritmos tienen una interpretación clara, otros funcionan como una caja negra y podemos utilizar enfoques como LIME o SHAP para derivar algunas interpretaciones.
En este artículo, me gustaría centrarme en la interpretación de los coeficientes del modelo de regresión más básico, es decir, la regresión lineal, incluyendo las situaciones en las que las variables dependientes/independientes han sido transformadas (en este caso hablo de la transformación logarítmica).
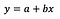
Supongo que el lector está familiarizado con la regresión lineal (si no hay muchos buenos artículos y posts en Medium), así que me centraré únicamente en la interpretación de los coeficientes.
La fórmula básica de la regresión lineal se puede ver arriba (he omitido los residuos a propósito, para mantener las cosas simples y al punto). En la fórmula, y denota la variable dependiente y x es la variable independiente. Para simplificar, vamos a suponer que se trata de una regresión univariante, pero los principios obviamente también son válidos para el caso multivariante.
Para ponerlo en perspectiva, digamos que después de ajustar el modelo recibimos:
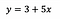
Intercepto (a)
Desglosaré la interpretación del intercepto en dos casos:
- x es continua y centrada (al restar la media de x de cada observación, la media de x transformada se convierte en 0) – la media de y es 3 cuando x es igual a la media muestral
- x es continua pero no centrada – la media de y es 3 cuando x = 0
- x es categórica – la media de y es 3 cuando x = 0 (esta vez indicando una categoría, más adelante)
Coeficiente (b)
- x es una variable continua
Interpretación: un aumento de una unidad en x da lugar a un aumento de la media de y en 5 unidades, manteniéndose constantes las demás variables.
- x es una variable categórica
Esto requiere un poco más de explicación. Digamos que x describe el género y puede tomar valores (‘hombre’, ‘mujer’). Ahora convirtámosla en una variable ficticia que toma valores 0 para los hombres y 1 para las mujeres.
Interpretación: la media de y es mayor en 5 unidades para las mujeres que para los hombres, manteniendo constantes todas las demás variables.
Modelo de nivel logarítmico
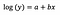
Típicamente utilizamos la transformación logarítmica para acercar los datos periféricos de una distribución positivamente sesgada al grueso de los datos, con el fin de que la variable se distribuya normalmente. En el caso de la regresión lineal, una ventaja adicional de utilizar la transformación logarítmica es la interpretabilidad.
Como antes, digamos que la fórmula siguiente presenta los coeficientes del modelo ajustado.
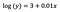
Intercepto (a)
La interpretación es similar a la del caso vainilla (nivel), sin embargo, tenemos que tomar el exponente del intercepto para la interpretación exp(3) = 20,09. La diferencia es que este valor representa la media geométrica de y (a diferencia de la media aritmética en el caso del modelo de niveles).
Coeficiente (b)
Los principios son de nuevo similares a los del modelo de niveles cuando se trata de interpretar variables categóricas/numéricas. De forma análoga al intercepto, tenemos que tomar el exponente del coeficiente: exp(b) = exp(0,01) = 1,01. Esto significa que un aumento unitario de x provoca un aumento del 1% en la media (geométrica) de y, manteniendo constantes todas las demás variables.
Dos cosas que vale la pena mencionar aquí:
- Hay una regla general a la hora de interpretar los coeficientes de un modelo de este tipo. Si abs(b) < 0,15 es bastante seguro decir que cuando b = 0,1 observaremos un aumento del 10% en y para un cambio unitario en x. Para los coeficientes con un valor absoluto mayor, se recomienda calcular el exponente.
- Cuando se trata de variables en rango (como un porcentaje) es más conveniente para la interpretación multiplicar primero la variable por 100 y luego ajustar el modelo. De esta manera la interpretación es más intuitiva, ya que aumentamos la variable en 1 punto porcentual en lugar de 100 puntos porcentuales (de 0 a 1 inmediatamente).
Modelo logarítmico
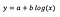
Supongamos que tras ajustar el modelo recibimos:

La interpretación del intercepto es la misma que en el caso del modelo de niveles.
Para el coeficiente b – un aumento del 1% en x resulta en un aumento aproximado de la media de y en b/100 (0,05 en este caso), manteniéndose constantes todas las demás variables. Para obtener la cantidad exacta, tendríamos que tomar b× log(1,01), que en este caso da 0,0498.
Modelo log-log
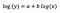
Supongamos que después de ajustar el modelo recibimos:
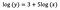
De nuevo me centro en la interpretación de b. Un aumento del 1% en x da lugar a un aumento del 5% en la media (geométrica) de y, manteniendo constantes todas las demás variables. Para obtener la cantidad exacta, tenemos que tomar
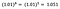
que es ~5,1%.
Conclusiones
Espero que este artículo le haya dado una visión general de cómo interpretar los coeficientes de la regresión lineal, incluyendo los casos en que algunas de las variables han sido transformadas logarítmicamente. Como siempre, cualquier comentario constructivo es bienvenido. Puedes ponerte en contacto conmigo en Twitter o en los comentarios.




