Léxico de las bombas centrífugas
Las pérdidas de carga son el resultado de la fricción de la pared en todo tipo de tuberías y de la resistencia local al flujo, por ejemplo en válvulas y accesorios (véase también Pérdida de presión).
Velocidades de flujo recomendadas
- Para agua fría:
Línea de aspiración 0.7-1,5 m/s
Línea de descarga 1,0-2,0 m/s - Para agua caliente:
Línea de aspiración 0,5-1,0 m/s
Línea de descarga 1,5-3,5 m/s
La ecuación para la pérdida de carga de un flujo en una longitud recta de tubería con sección circular es:
λ Factor de fricción de la tubería
L Longitud de la tubería en m
d Diámetro interior de la tubería en m
v Velocidad del flujo en una sección transversal en m/s
(= 4 Q / π d2 con Q en m3/s)
g Aceleración debida a la gravedad en m/s2
Ver Fig. 1 y 4 Pérdida de carga
El factor de fricción de la tubería se estableció experimentalmente. Sólo depende del estado de flujo del fluido manipulado y de la rugosidad relativa (d/k) de las tuberías por las que circula el fluido. Para secciones transversales de tuberías no circulares se aplica el diámetro equivalente en términos fluidomecánicos (d):
A Sección transversal en m2
U Circunferencia de la sección transversal mojada en m
(no se considera la superficie libre de un canal abierto)
El estado de flujo se determina por el número de Reynolds (Re) según las leyes de afinidad. Lo siguiente se aplica a las tuberías circulares:
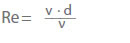
v Velocidad del flujo en una sección transversal en m/s
(= 4 Q / π d2 con Q en m3/s)
ν Viscosidad cinemática en m2/s
(para agua a 20 °C: 1.00 – 10 – 6 m2/s)
d Diámetro interior de la tubería en m
Ver Fig. 4 Pérdida de carga
Para tuberías hidráulicamente lisas, como las de metal estirado o plástico (por ejemplo, PE o PVC), o en caso de flujo laminar, puede calcularse el factor de fricción de la tubería (λ). Para un flujo laminar en una tubería con un número de Reynolds inferior a 2320, el factor de fricción de la tubería es independiente de la rugosidad:
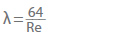
Si el flujo es turbulento, o el número de Reynolds superior a 2320, el factor de fricción de la tubería en tuberías hidráulicamente lisas puede representarse mediante una ecuación empírica según Eck (debido a que las desviaciones son inferiores al 1 % si el número de Reynolds es inferior a 108).
El factor de fricción de la tubería (λ) también depende de otro parámetro adimensional, es decir, de la rugosidad relativa de la superficie interior de la tubería (d/k). Ambos deben especificarse en la misma unidad (por ejemplo, mm).
Ver Fig. 1 Pérdida de carga
(k) es la rugosidad absoluta media de la superficie interior de la tubería para la que existen valores aproximados en función del material y los procesos de fabricación. Véase la Fig. 2 Pérdida de carga
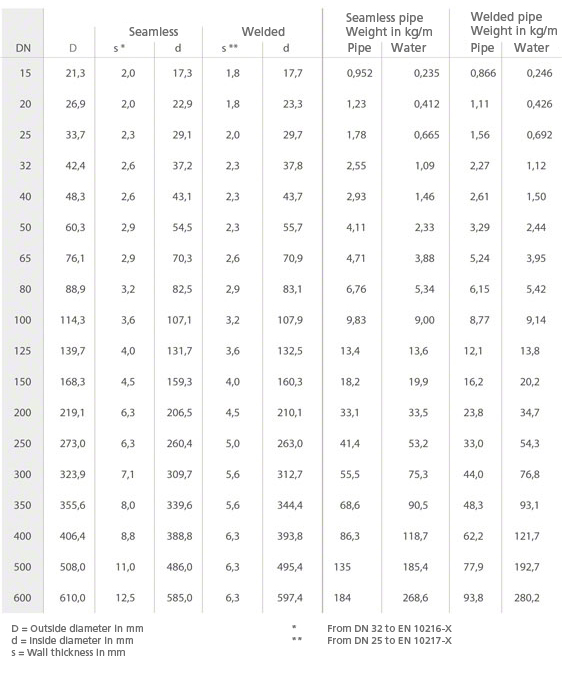Fig. 2 Pérdida de carga: Estimaciones de las alturas medias de pico a valle k (rugosidad absoluta) de las tuberías
Por encima de la curva límite, el factor de fricción de la tubería (λ) depende únicamente de la rugosidad relativa de la tubería (d/k). Ver Fig. 1 Pérdida de carga
Para esta región puede utilizarse la siguiente ecuación empírica de Moody:
Para un uso práctico, la pérdida de carga (HL) por 100 m de tubería recta de acero se muestra en el diagrama en función del caudal (Q) y del diámetro interior de la tubería (d).
Ver Fig. 3 Pérdida de carga
Los valores son válidos sólo para agua fría y limpia o para fluidos con la misma viscosidad cinemática, para tuberías completamente llenas y para una rugosidad absoluta de la superficie interior de la tubería de k = 0.05 mm.
Dimensiones, pesos, llenado de agua para tuberías nuevas de acero sin costura o soldadas longitudinalmente
Ver Anexo, Pérdida de carga, Fig. 4
A continuación se demostrará el efecto de un aumento de la rugosidad de la superficie k para un conjunto de rangos de parámetros frecuentemente utilizados (diámetro nominal DN = 50 a 300, velocidad de flujo v = 0,8 a 3,0 m/s). Véase la Fig. 3 Pérdida de carga
La región de color azul claro corresponde a la región marcada de forma similar para una rugosidad media absoluta de k = 0,05 mm.
Véase la Fig. 1 Pérdida de carga
Para una rugosidad aumentada en un factor de 6 (tubería de acero vieja ligeramente incrustada con k = 0,30 = 300 μm (0.30 mm), los factores de fricción de la tubería (y las pérdidas de carga proporcionales asociadas) en la región azul oscuro son sólo un 25 – 60 % más altos que antes.
Ver Fig. 1 Pérdida de carga
Para las tuberías de aguas residuales debe tenerse en cuenta el aumento de la rugosidad causado por la suciedad. En el caso de las tuberías sometidas a una incrustación extrema, la pérdida de carga real sólo puede determinarse experimentalmente. Las desviaciones del diámetro nominal modifican considerablemente la pérdida de carga, ya que el diámetro interior de la tubería figura en la ecuación a la 5ª potencia.
Una reducción del 5 % del diámetro interior, por ejemplo, conduce a un aumento de la pérdida de carga de hasta un 30 %. Por lo tanto, es importante que el diámetro interior no se sustituya simplemente por el diámetro nominal en los cálculos.
Las pérdidas de carga en tuberías de plástico o en tuberías metálicas lisas estiradas son muy bajas gracias a las superficies lisas de las tuberías. Las pérdidas de carga establecidas son válidas para el agua a 10 °C. A otras temperaturas, la pérdida de las tuberías de plástico debe multiplicarse por un factor de corrección de la temperatura especificado para tener en cuenta su mayor expansión térmica. En el caso de aguas residuales u otras aguas no tratadas, debe tenerse en cuenta una pérdida de carga adicional del 20-30 % para posibles depósitos.
Pérdidas de carga para tuberías de plástico y de metal estirado liso
Ver anexo, Pérdida de carga, Fig. 5
Pérdidas de carga en válvulas y accesorios
La pérdida de carga (HL) en válvulas y accesorios viene dada por:
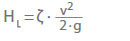
ζ Coeficiente de pérdida
Ver Figs. 6 a 12 Pérdida de carga
v Velocidad del flujo en un área de sección transversal característica A
(por ejemplo, en la boquilla) en m/s
g Aceleración debida a la gravedad 9,81 m/s2
Fig. 6 Pérdida de carga: Diagrama esquemático de diseños de válvulas
Fig. 11 Pérdida de carga: Influencia en el coeficiente de pérdida ζ del redondeo del lado interior y exterior de los codos en conductos cuadrados
Fig. 12 Pérdida de carga: Coeficientes de pérdida ζ para válvulas de mariposa, de globo y de compuerta en función del grado de apertura
Las pérdidas atribuibles al enderezamiento de las perturbaciones del flujo a lo largo de una longitud de tubería equivalente a 12 x DN aguas abajo de la válvula se incluyen en los coeficientes de pérdida de acuerdo con la directriz VDI/VDE 2173. Los valores se aplican a las válvulas que tienen un flujo de aproximación constante, están completamente abiertas y funcionan con agua fría. Dependiendo de las condiciones de flujo de entrada y salida, de los modelos de válvulas y de los objetivos de desarrollo (por ejemplo, válvulas económicas o de bajo consumo), los valores de pérdida pueden variar drásticamente. Véase el anexo, Pérdida de carga, Fig. 7
A menudo se utiliza el valor kv en lugar del coeficiente de pérdida (ζ) al calcular la pérdida de presión para el agua en las válvulas:
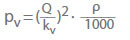
El valor kv es el caudal en m3/h que resultaría de una caída de presión pv = 1 bar a través de la válvula para el agua fría. Describe la correlación entre la pérdida de presión (pL) en bar y el caudal (Q) en m3/h. Conversión a coeficiente de caudal ζ para agua fría:
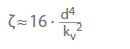
d Diámetro de referencia (nominal) de la válvula en cm
Para el cálculo de las pérdidas de carga en accesorios, los accesorios de derivación y los adaptadores requieren un enfoque diferente. Véanse las figuras 9 y 10 Pérdidas de carga
Fig. 9 Pérdidas de carga: Coeficientes de pérdida ζ para accesorios 
Fig. 10 Pérdida de carga: Coeficientes de pérdida ζ para adaptadores
Para todos los accesorios hay que diferenciar entre dos formas de pérdida de carga:
- Pérdidas de presión irreversibles (reducción de la presión)
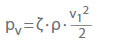
pv Pérdida de presión en Pa
ζ Coeficiente de pérdida
ρ Densidad en kg/m3
v Velocidad de flujo en una sección transversal-sección en m/s
- Cambios de presión reversibles del flujo sin fricción según la ecuación de Bernoulli
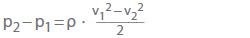
Para flujos acelerados como reducciones del diámetro de la tubería, (p2 – p1) es siempre negativo; para los flujos desacelerados, como las expansiones de las tuberías, siempre es positivo. Cuando se calcula el cambio neto de presión como la suma aritmética de pL y (p2 – p1), siempre se deben restar las pérdidas de presión irreversibles.
Influencia de los fluidos de alta viscosidad en la curva característica del sistema
Como las leyes de la dinámica de los fluidos conservan su validez para todos los fluidos newtonianos, las ecuaciones y los diagramas para calcular los factores de fricción de las tuberías y los coeficientes de pérdida de las válvulas también son aplicables a los fluidos viscosos con una viscosidad superior a la del agua.
Al calcular el número de Reynolds Re = v – d / ν , hay que sustituir simplemente la viscosidad cinemática de los fluidos viscosos νz por la viscosidad del agua νz.
De este modo se obtiene un número Re más bajo y, según la Fig. 1 Pérdida de carga, un mayor coeficiente de fricción de la tubería λz (Nota: la influencia de la rugosidad de la pared puede ignorarse ahora a menudo debido al mayor espesor de la capa límite en el flujo).
Todas las pérdidas de carga en las tuberías y válvulas calculadas para el agua deben extrapolarse utilizando la relación λz/λw.
La figura 13 Pérdida de carga también es adecuada para el uso práctico general: el factor de fricción de la tubería λz puede determinarse rápidamente en función del caudal Q, del diámetro interior de la tubería d y de la viscosidad cinemática νz. No obstante, hay que tener en cuenta que el coeficiente λw de este diagrama sólo es válido para tuberías hidráulicamente lisas (es decir, ¡no para tuberías rugosas!). El correspondiente λw puede utilizarse para calcular la relación λz/λw.
Como la componente estática de la curva característica del sistema Hsys , véase la Fig. 1 Curva característica del sistema y la Fig. 2 Cabeza, no se ve afectada por la viscosidad, la componente dinámica de la curva característica del sistema para el agua puede volver a dibujarse como una parábola más pronunciada para un fluido viscoso.
Influencia de los fluidos no newtonianos en la curva característica del sistema
Como las curvas de flujo no son líneas rectas de viscosidad lineal constante, el cálculo de las pérdidas de carga es muy engorroso. En este caso, el cálculo de las pérdidas se basa en la experiencia con fluidos concretos.