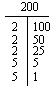Números primos
Todos los números enteros se clasifican como primos o compuestos, con las excepciones del cero y el uno, que son casos especiales. Veamos la diferencia entre números primos y compuestos. Los números primos tienen exactamente dos factores, uno y el propio número. Si conoce las reglas de divisibilidad (tratadas en la siguiente sección), determinar los números primos del 1 al 100 es una tarea relativamente fácil. Aquí están los números primos hasta el 25:
2, 3, 5, 7, 11, 13, 17, 19, 23
No hay un patrón para encontrar todos los números primos que existen, aunque los matemáticos han encontrado números primos con casi ocho millones de dígitos. Este es uno de los grandes misterios matemáticos que quedan para los matemáticos.
Los números compuestos tienen más de dos factores pero no un número infinito de factores. Todos los números pares (excepto el número dos) son compuestos, ya que todos pueden dividirse por dos.
El cero no es ni primo ni compuesto. Como cualquier número por cero es igual a cero, hay un número infinito de factores para un producto de cero. Un número compuesto debe tener un número finito de factores.
El uno tampoco es primo ni compuesto. La única forma de obtener un producto de uno es multiplicando 1 x 1. Pero los factores duplicados sólo se cuentan una vez, así que uno sólo tiene un factor. (Un número primo tiene exactamente dos factores, por lo que el uno no puede ser primo.)
Una pregunta típica de examen te haría identificar qué número de una lista es primo (o compuesto o ninguno).
Prueba esta:
Pregunta
¿Cuál de los siguientes es un número primo?
- 33
- 45
- 41
- 51
Responde
La respuesta correcta es C. El cuarenta y uno es un número primo; los otros números son compuestos. Ten cuidado con el 51-sale de 3 x 17.
Reglas de divisibilidad
Las reglas de divisibilidad son herramientas que te ayudan a hacer menos divisiones. Las reglas de divisibilidad pueden ayudarte a determinar si un número es primo o compuesto, así como a descomponer los números compuestos en sus factores primos, el tema que trataremos a continuación.
Las reglas de divisibilidad son atajos que te indican si un número es divisible por otro. Las reglas cubren la división por los números del 2 al 10 y te permiten comprobar los números hasta el 100. Haz clic en los números de la tabla.
| Reglas de divisibilidad | ||
|---|---|---|
| 2 | 3 | 4 |
| 5 | 6 | 7 |
| 8 | 9 | 10 |
Pregunta
¿Cuál de los siguientes números no es divisible por 3?
- 4,873
- 7,521
- 12,642
- 25,308
Descubre la respuesta
La respuesta correcta es la A. La forma rápida de hacer este problema es utilizar la regla de divisibilidad; sumar los dígitos de cada número buscando el que no es múltiplo de tres. La forma lenta sería hacer cada problema de división-incluso en una calculadora, este método tomará más tiempo!
Factorización de Primas: T’s y Árbol
Este es otro tema en el que quizás no hayas pensado desde la escuela media. El Teorema Fundamental de la Aritmética establece que todo número compuesto puede descomponerse en un único producto de números primos.
La factorización de primos es el proceso que encuentra los productos de números primos de un número compuesto dado. La factorización de números primos es útil por sí misma, pero muchas de sus aplicaciones implican fracciones, que cubriremos más adelante.
Es posible que pueda encontrar la factorización de números primos de un número en su cabeza. Por ejemplo, 12 es 2 x 2 x 3 o 22 x 3. (Las factorizaciones primarias a menudo se representan con exponentes.)
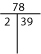
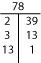
Si no puedes encontrar la factorización primaria mentalmente, prueba con un Factor-T o un Árbol de Factores.
Revisión
- Los números primos tienen exactamente dos factores, uno y él mismo.
- Los números compuestos tienen más de dos factores pero no un número infinito.
- Cero y uno no son ni primos ni compuestos.
- Las reglas de divisibilidad son atajos que pueden ayudarte a determinar los factores de un número.
- Todo número compuesto puede escribirse como un producto único de números primos, lo que se llama la factorización primaria de un número.
- Dos métodos prácticos para encontrar factorizaciones primarias son los factores T y los árboles de factores.