Skewness – pikaesittely, esimerkkejä ja kaavoja
Skewness on luku, joka kertoo, missä määrin
muuttuja on epäsymmetrisesti jakautunut.
- Positiivinen (oikea) vinouma Esimerkki
- Negatiivinen (vasen) vinouma Esimerkki
- Populaation vinouma – Kaava ja laskenta
- Otoksen vinouma -. Kaava ja laskenta
- Skewness in SPSS
- Skewness – Implications for Data Analysis
Positiivinen (oikea) Skewness Esimerkki
Tutkijalla on 1,000 ihmistä suorittamaan joitakin psykologisia testejä. Testin 5 osalta testipisteiden vinous = 2,0. Näiden pisteiden histogrammi on esitetty alla.
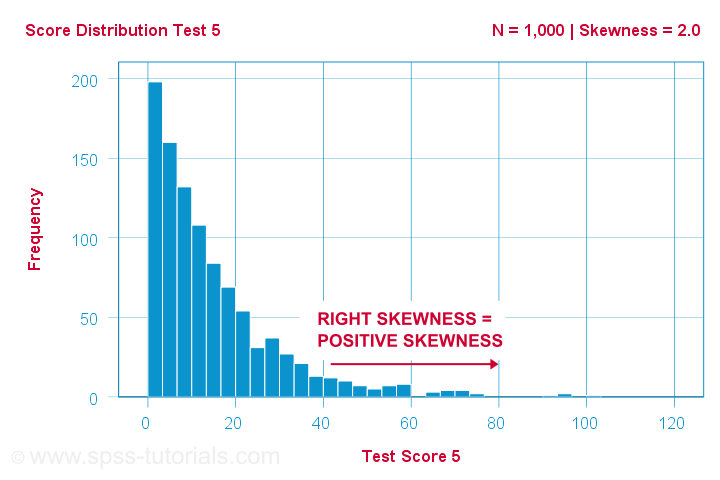
Histogrammi osoittaa hyvin epäsymmetrisen frekvenssijakauman. Suurin osa ihmisistä saa 20 pistettä tai vähemmän, mutta oikeanpuoleinen häntä ulottuu noin 90 pisteeseen. Tämä jakauma on oikealle vino.
Jos liikumme x-akselia pitkin oikealle, siirrymme 0:sta 20:een, 40 pisteeseen ja niin edelleen. Kuvaajan oikeaa puolta kohti pisteet muuttuvat siis positiivisemmiksi. Siksi oikeanpuoleinen vinous on positiivinen vinousjoka tarkoittaa vinoutta > 0. Tässä ensimmäisessä esimerkissä on vinous = 2,0, kuten kuvaajan oikeassa yläkulmassa näkyy. Pisteet ovat vahvasti positiivisesti vino.
Negatiivinen (vasen) vinous Esimerkki
Toisella muuttujalla -testin 2- pisteet osoittautuvat vinoksi = -1.0. Niiden histogrammi on esitetty alla.

Suurin osa pistemääristä on noin 60 ja 100 välillä. Vasen häntä on kuitenkin jonkin verran venynyt. Tämä jakauma on siis vasemmalle vino.
Oikea: vasemmalle, vasemmalle. Jos seuraamme x-akselia vasemmalle, siirrymme kohti negatiivisempia pistemääriä. Siksi vasemmanpuoleinen vinous on negatiivinen vinous.Ja todellakin, vinous = -1,0 näille pisteille. Niiden jakauma on vasemmalle vino. Se on kuitenkin vähemmän vino -tai symmetrisempi- kuin ensimmäinen esimerkkimme, jonka skewness = 2.0.
Symmetrinen jakauma merkitsee nollaa skewnessia
Loppujen lopuksi symmetrisillä jakaumilla on skewness = 0. Testin 3 pisteet -joka on skewness = 0.1- tulevat lähelle sitä.

Havainnoidut jakaumat ovat harvoin täsmälleen symmetrisiä. Tämä on nähtävissä lähinnä joidenkin teoreettisten otantajakaumien kohdalla. Esimerkkejä ovat
- (standardi)normaalijakauma;
- t-jakauma ja
- binomijakauma, jos p = 0.5.
Nämä jakaumat ovat kaikki täsmälleen symmetrisiä ja siten vinous = 0.000…
Populaation vinous – kaava ja laskenta
Jos haluat laskea vinousarvot yhdelle tai useammalle muuttujalle, jätä laskutoimitukset jollekin ohjelmistolle. Mutta -täydellisyyden vuoksi- luettelen kaavat kuitenkin.
Jos aineistosi sisältää koko populaatiosi, laske populaation vinous seuraavasti:
$$$Populaatio\;skewness = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$$$
jossa
- \(X_i\) on kukin yksittäinen pisteytys;
- \(\mu\) on populaation keskiarvo;
- \(\sigma\) on populaation keskihajonta ja
- \(N\) on populaation koko.
Esimerkki laskutoimituksesta, jossa käytetään tätä kaavaa, löytyy tästä Googlesheetistä (näkyy alla).
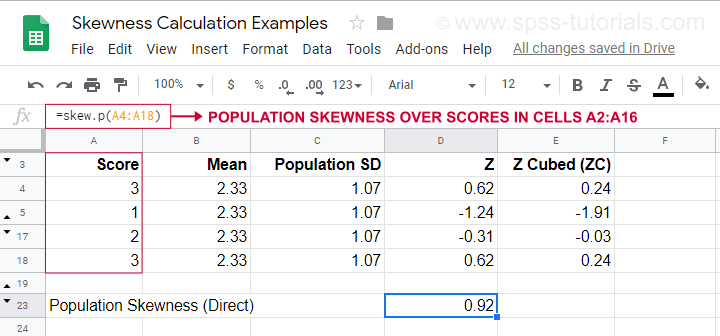
Se näyttää myös, miten populaation vinous saadaan suoraan käyttämällä=SKEW.P(…)missä ”.P” tarkoittaa ”populaatiota”. Tämä vahvistaa manuaalisen laskelmamme tuloksen. Valitettavasti SPSS ja JASP eivät laske populaation vinoutta: molemmat rajoittuvat otoksen vinouteen.
Otoksen vinous – Kaava ja laskenta
Jos aineistosi sisältää yksinkertaisen satunnaisotoksen jostain populaatiosta, käytä
$$Sample\;skewness = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$
jossa
- \(X_i\) on jokainen yksittäinen pistemäärä;
- \(\overline{X}\) on otoksen keskiarvo;
- \(S\) on otoksen keskihajonta ja
- \(N\) on otoskoko.
Esimerkkilaskelma on esitetty tässä Googlesheetissä (näkyy alla).
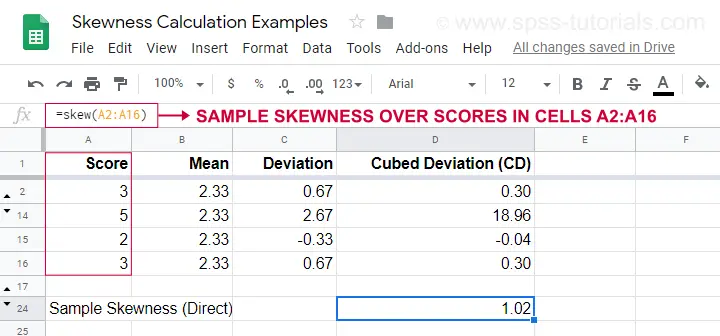
Helpompi vaihtoehto otoksen vinouden saamiseksi on käyttää=SKEW(…).joka vahvistaa manuaalisen laskelmamme tuloksen.
Vinouma SPSS:ssä
Aluksi, ”vinouma” SPSS:ssä viittaa aina otosvinoumaan: se olettaa hiljaa, että aineistossasi on otos eikä koko perusjoukko. Sen saamiseen on paljon vaihtoehtoja. Suosikkini on MEANS, koska syntaksi ja tulostus ovat puhtaita ja yksinkertaisia. Alla olevat kuvakaappaukset opastavat sinua.

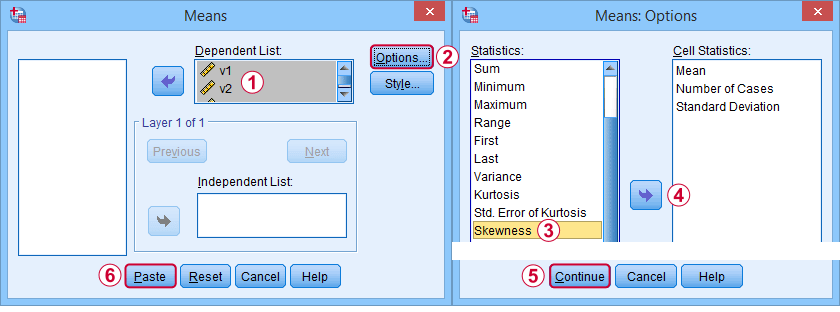
Syntaksi voi olla niinkin yksinkertainen kuinmeans v1 to v5
/cells skew.Erittäin kattava taulukko – mukaan lukien keskiarvot, keskihajonnat, mediaanit ja paljon muuta – ajetaanmeans v1 to v5
/cells count min max mean mediaani stddev skew kurt.Tulos on esitetty alla.
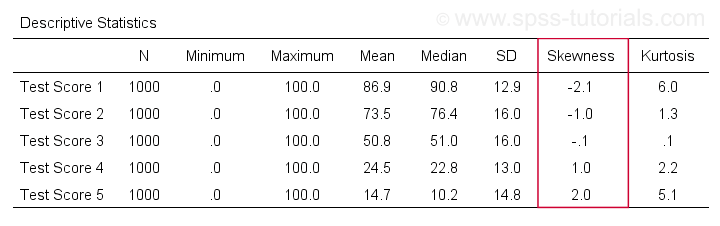
Skewness – Implications for Data Analysis
Monet analyysit -ANOVA, t-testit, regressio ja muut- edellyttävät normaalisuusolettamaa: muuttujien tulisi olla normaalisti jakautuneita populaatiossa. Normaalijakauman vinous = 0. Joten huomattavan vinouden havaitseminen joissakin otosaineistoissa viittaa siihen, että normaalisuusolettamaa on rikottu.
Tällaiset normaalisuuden rikkomiset eivät ole ongelma, jos otoskoko on suuri – sanotaan N > 20 tai 25 tai noin. Tällöin useimmat testit ovat kestäviä tällaisia rikkomuksia vastaan. Tämä johtuu keskeisestä raja-arvoteoriasta. Lyhyesti sanottuna, kun otoskoko on suuri, vinous
ei ole todellinen ongelma tilastollisille testeille.Vinous liittyy kuitenkin usein suuriin keskihajontoihin. Nämä voivat johtaa suuriin keskivirheisiin ja pieneen tilastolliseen tehoon. Näin ollen huomattava vinous voi vähentää mahdollisuutta hylätä jokin nollahypoteesi jonkin vaikutuksen osoittamiseksi. Tällöin ei-parametrinen testi voi olla viisaampi valinta, koska sen teho voi olla suurempi.Normaalisuusrikkomukset ovat todellinen uhka
pienille otoskoolle, joiden koko on -vaikkapa- N < 20 tai noin. Kun otoskoko on pieni, monet testit eivät ole kestäviä normaalisuusolettaman rikkomista vastaan. Ratkaisu on -jälleen kerran- ei-parametrisen testin käyttäminen, koska nämä eivät vaadi normaalisuutta.
Lopuksi, mutta ei vähäisimpänä, ei ole olemassa mitään tilastollista testiä, jolla voitaisiin tutkia, onko populaation vinous = 0. Epäsuora tapa testata tätä on normaalisuustestit, kuten
- Kolmogorov-Smirnovin normaalisuustestit ja
- Shapiro-Wilkin normaalisuustestit.
Mutta silloin, kun normaalisuutta todella tarvitaan – pienillä otoskokoluokilla – tällaisilla testeillä on heikko teho: ne eivät välttämättä saavuta tilastollista merkitsevyyttä, vaikka poikkeamat normaalisuudesta olisivat vakavia. Näin ollen ne lähinnä antavat väärän turvallisuuden tunteen.




