Synteettinen jakomenetelmä
Minun täytyy sanoa, että synteettinen jako on ”hauskin” tapa jakaa polynomeja. Siinä on vähemmän vaiheita vastauksen saamiseksi verrattuna polynomien pitkään jakomenetelmään. Tällä oppitunnilla käyn läpi viisi (5) esimerkkiä, joiden avulla toivottavasti tutustut perusmenettelyihin, joilla polynomien jakaminen synteettisellä jakomenetelmällä onnistuu.
Muistettavaa:
- Varmista, että jakolasku on vakiomuodossa. Se tarkoittaa, että potenssit ovat pienenevässä järjestyksessä.
- Jakaja on oltava muodossa x – \vasen( c \oikea).
Esimerkkejä siitä, miten polynomeja jaetaan synteettisellä jaolla
Esimerkki 1: Jaetaan alla oleva polynomi.
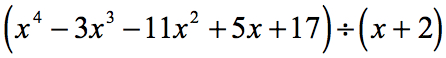
Tarkastellaan annettua ongelmaa uudelleen ja tehdään tarvittaessa tarvittavat korjaukset.
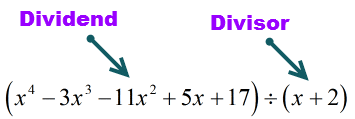
Jakaja (jaettava aine) on vakiomuodossa, koska eksponentit ovat laskevassa järjestyksessä. Se on hyvä!
Jakaja on kirjoitettava uudelleen muotoon
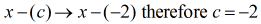
Tässä vaiheessa voin nyt asettaa synteettisen jaon poimimalla osingon kertoimet ja asettamalla ne sitten riviin.
Suoraan vasemmalle puolelle sijoitetaan ”laatikon” sisälle arvo c = – 2.
Viimeiseksi rakennetaan vaakasuora viiva heti osingon kertoimien alapuolelle.
Vaiheet:
1. Pudota ensimmäinen kerroin vaakaviivan alapuolelle.
2. Kerro tämä pudottamasi luku ”laatikossa” olevalla luvulla. Mikä sen tulo onkaan, aseta se vaakaviivan yläpuolelle heti toisen kertoimen alapuolelle.
3. Laske numerosarake yhteen ja aseta summa sitten suoraan vaakaviivan alapuolelle.
4. Toista prosessia, kunnes sarakkeet loppuvat kesken.
Katso alla oleva animaatioratkaisu:
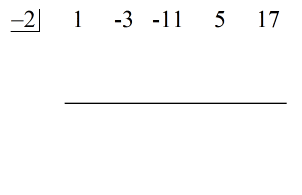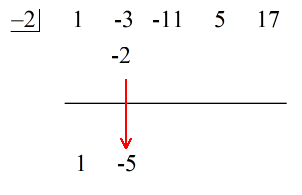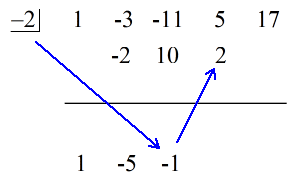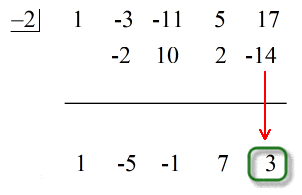
Viimeinen vaakaviivan alapuolella oleva luku on aina jäännös! Tämän tehtävän jäännös on 3.
Miten siis esitämme lopullisen vastauksemme?
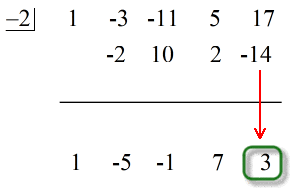
- Näytä lopullinen vastauksesi muodossa
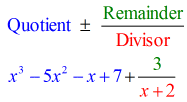
Huomaa, että vaakasuoran viivan alapuolella olevat luvut viimeistä (jäännös) lukuun ottamatta ovat Kertoimen kertoimia.
Lisäksi kvintientin muuttujien eksponentit ovat kaikki pienentyneet 1:llä.
Esimerkki 2: Jaa polynomi.
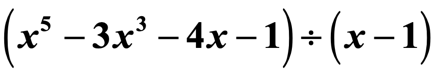
Tämä ei ole temppukysymys. Huomaa, että lainaajassa ei ole kaikkia muuttujan x eksponentteja.
Huomaa, että meiltä puuttuvat {x^4} ja {x^2}. Jotta kaikki muuttujan x kertoimet olisivat mukana vähenevässä potenssissa, meidän pitäisi kirjoittaa alkuperäinen ongelma uudelleen näin. Liitä nollat näihin puuttuviin x:iin. Ilmaise myös jakaja muodossa x – (c), josta käy selvästi ilmi c:n arvo, eli c = + 1.
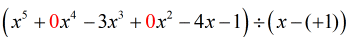
Tässä vaiheessa voin nyt asettaa luvut, jotta voin jatkaa prosessia.
Vaiheet:
1. Pudota ensimmäinen kerroin vaakasuoran viivan alapuolelle.
2. Kerro tuo pudottamasi luku ”laatikossa” olevalla luvulla. Mikä sen tulo onkaan, aseta se vaakaviivan yläpuolelle heti toisen kertoimen alapuolelle.
3. Laske numerosarake yhteen ja aseta summa suoraan vaakaviivan alapuolelle.
4. Toista prosessia, kunnes sarakkeet loppuvat.
Katso alla oleva animoitu ratkaisu:
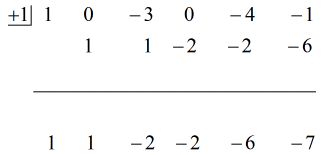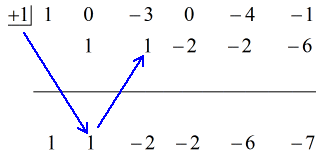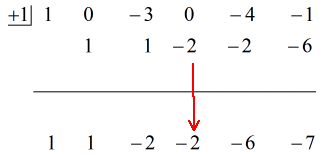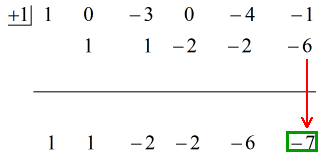
Sijoittamalla lopullisen vastauksen muotoon
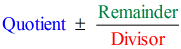
saamme
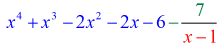
Esimerkki 3: Jaa alla oleva polynomi.
\left( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Tästä tulee mielenkiintoisempaa! Osamäärä näyttää varmasti kamalalta, koska siitä puuttuu paljon. Sen lisäksi, että siitä puuttuu joitakin x:iä, jotka ovat {x^3} ja {x^2}, myös vakio on kadonnut.
Korjatakseni tämän kirjoitan alkuperäisen ongelman uudelleen siten, että kaikki x:t otetaan huomioon. Mutta mikä tärkeintä, älä unohda sisällyttää puuttuvaa vakiota, joka on nolla.
”Uuden ja parannetun” ongelman pitäisi näyttää tältä:
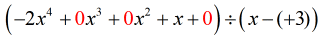
Tästä eteenpäin edetään tavalliseen tapaan.
Vaiheet:
1. Pudota ensimmäinen kerroin vaakaviivan alapuolelle.
2. Kerro tuo pudottamasi luku ”laatikossa” olevalla luvulla. Mikä sen tulo onkaan, aseta se vaakaviivan yläpuolelle heti toisen kertoimen alapuolelle.
3. Laske numerosarake yhteen ja aseta summa suoraan vaakaviivan alapuolelle.
4. Toista prosessia, kunnes sarakkeet loppuvat.
Katso alla oleva animoitu ratkaisu:
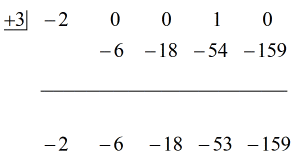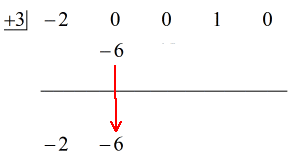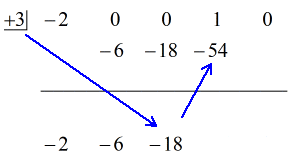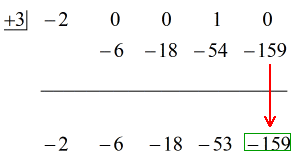
Okei, lopullinen vastaus tähän on
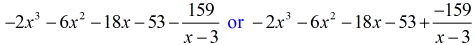
Voit kirjoittaa lopullisen vastauksen kahdella tavalla. Ensimmäisessä käytetään miinus- tai vähennysmerkkiä osoittamaan, että jäännös on negatiivinen. Toinen tapa on käyttää +-symbolia, mutta liittää negatiivinen symboli osoittajaan. Ne tarkoittavat samaa asiaa!
Esimerkki 4: Jaa alla oleva polynomi.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Älä lannistu tästä ongelmasta. Tämä on itse asiassa melko helppoa varsinkin nyt, kun olet jo käynyt läpi muutaman esimerkin. Muista aina ”täyttää puuttuvat osat”, eikö?
Katsele ositusta ja sinun pitäisi olla samaa mieltä siitä, että puuttuvat osat ovat {x^4}, {x^3}, {x^2} ja x.
Kirjoittamalla alkuperäisen ongelman uudelleen, joka on synteettisen jakamisen valmis, saamme…
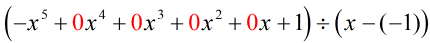
Puuttuvat x:t täytetään nollilla ja ratkaistaan eksplisiittisesti c = -1.
Vaiheet:
1. Pudota ensimmäinen kerroin vaakasuoran viivan alapuolelle.
2. Kerro tuo pudottamasi luku ”laatikossa” olevalla luvulla. Mikä sen tulo onkaan, aseta se vaakaviivan yläpuolelle heti toisen kertoimen alapuolelle.
3. Laske numerosarake yhteen ja aseta summa suoraan vaakaviivan alapuolelle.
4. Laske se yhteen. Toista prosessia, kunnes yhteenlaskettavat sarakkeet loppuvat.
Katso alla oleva animoitu ratkaisu:
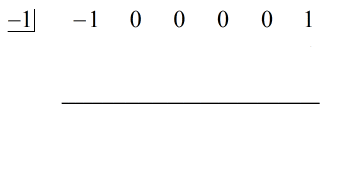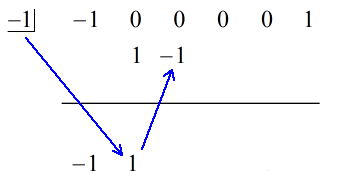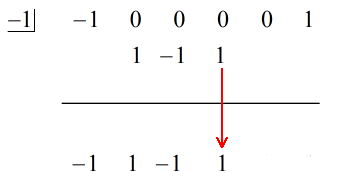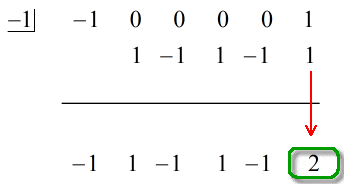
Vaakaviivan alapuolella oleva viimeinen luku on aina jäännös. Älä unohda sitä. Tässä tapauksessa jäännös on 2.
Lopullinen vastauksemme on
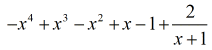
Esimerkki 5: Jaa polynomi binomilla.
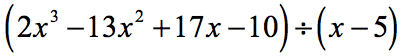
Tässä esimerkissä saamme jäännökseksi nolla. Kun näin tapahtuu, jakaja muuttuu jakolaskun tekijäksi. Toisin sanoen jakaja jakaa osingon tasan.
Tarkastelemalla ongelmaa näen, että puuttuvia komponentteja ei ole. Kaikki x:n potenssit on huomioitu, ja meillä on vakio. Hienoa! Tämä ongelma on itse asiassa valmis synteettiseen jakoon.
Vaiheet:
1. Pudota ensimmäinen kerroin vaakaviivan alapuolelle.
2. Kerro tuo pudottamasi luku ”laatikossa” olevalla luvulla. Mikä sen tulo onkaan, aseta se vaakaviivan yläpuolelle heti toisen kertoimen alapuolelle.
3. Laske numerosarake yhteen ja aseta summa suoraan vaakaviivan alapuolelle.
4. Toista prosessia, kunnes sarakkeet loppuvat.
Katso alla oleva animoitu ratkaisu:
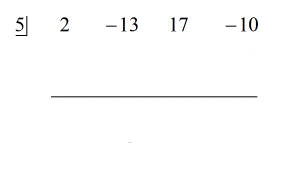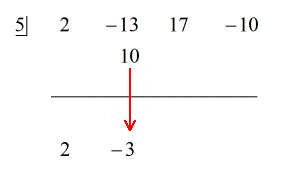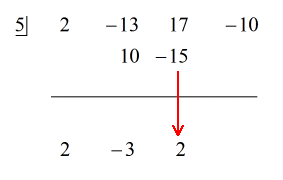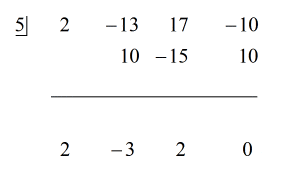
Koska jäännös on nolla, tämä tarkoittaa, että jakaja x – 5 on osingon tekijä
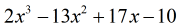
siten
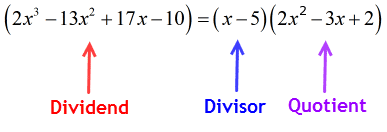
Harjoittelua työtaulukoiden avulla
Mahdollisesti sinua kiinnostaa myös:
Polynomien yhteen- ja vähennyslasku
Polynomien jakaminen pitkällä jakomenetelmällä
Kaksinimien kertominen FOIL-menetelmällä
Polynomien kertominen
.




