Todennäköisyys Johdanto: Todennäköisyys: Artikkelit ja videot ratkaisujen kanssa!

admin 0 Comments Articles

Todennäköisyys Johdanto: Todennäköisyys: Artikkelit ja videot ratkaisujen kanssa!

Nopanheitto, parkkipaikan löytäminen, korttivoitto; Nämä ovat vain muutamia tilanteita, joissa saatat haluta selvittää jonkin tapahtuman toteutumisen todennäköisyyden. Jos haluat tietää, miten todennäköisyys löydetään, sinun on ensin selvitettävä, millainen kysymys sinulla on. Esimerkiksi se, miten löydät tapahtuman toteutumisen todennäköisyyden, on eri asia kuin se, miten löydät todennäköisyyden sille, että ryhmän jäsenet valitsevat saman asian.

Jotkut todennäköisyydet on helppo tunnistaa, kuten nopan heittotodennäköisyyksien löytäminen tai korttipakasta valitseminen.

Kysymykset, joihin liittyy binomiteoria, on myös helppo tunnistaa. Tämäntyyppisissä kokeissa tapahtuman ainoat mahdolliset lopputulokset ovat ”Onnistuminen” tai ”Epäonnistuminen”: kuten kyllä/ei, kruunu/kruunu tai musta/valkoinen.

Muut kysymystyypit, joihin saatat törmätä, liittyvät ihmisiin, kuten:

• Henkilön valitseminen ryhmästä tai komiteasta.
• Todennäköisyys, että ryhmä valitsee saman asian.

Tapahtumat

Tahdotko selvittää yksinkertaisen tapahtuman toteutumisen todennäköisyyden? Kuten että sataa tai että löydät parkkipaikan keskustasta? Katso:
Todennäköisyys, että yksinkertainen tapahtuma tapahtuu.
Toisaalta, jos haluat täysin päinvastaista, katso:
Miten selvittää todennäköisyys, että tapahtuma EI tapahdu.

Kysytkö kysymyksesi siitä, että yksi tapahtuma tapahtuu toisen tapahtuman ollessa kyseessä? Kuten todennäköisyys löytää parkkipaikka, koska on pelipäivä, tai löytää tietty suosittu lelu mustana perjantaina? Jos näin on, katso:

• Jonkin tapahtuman todennäköisyys, kun otetaan huomioon toinen tapahtuma.
• Kahden tapahtuman esiintyminen yhdessä.

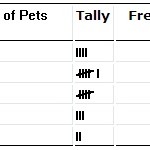
Tiheysjakaumataulukko.

Tiheysjakaumat

Onko sinulla taajuusjakauma, jonka kanssa voit työskennellä? Vai pystytkö tekemään taajuusjakaumataulukon annetuista tiedoista? Sinulla on esimerkiksi x kappaletta, joilla on tietty ominaisuus. Todennäköisyyden frekvenssijakauma.

Introduction to Probability: How-to Articles and Videos.

1. Permutaatiot ja yhdistelmät: How to Solve Problems
2. Probability Problems:
3. Probability of a and b.
4. Total Probability Rule.
5. Bayes Theorem Problems: Easy Solution Steps.
6. Prior Probability (including Uninformative and Conjugate).
7. How to Make a Probability Distribution from data.
8. How to find the Probability of Selecting a Person from a Group or Committee.
9. Miten löytää todennäköisyys sille, että tapahtuma EI tapahdu.
10. Todennäköisyysfrekvenssijakauma.
11. Miten löytää todennäköisyys sille, että yksinkertainen tapahtuma tapahtuu.
12. Sattumanvarainen tapahtuma: Todennäköisyys annettuna prosentteina.
13. Miten löydetään todennäköisyys sille, että ryhmän jäsenet valitsevat saman asian.
14. Miten löydetään todennäköisyys sille, että kaksi toisistaan riippuvaista tapahtumaa tapahtuu yhdessä.
15. Miten löydetään todennäköisyys sille, että tapahtuma tapahtuu toisen tapahtuman perusteella.
16. How to use a Probability Tree (Decision Tree) to Calculate Odds.
17. How to find the Probability of Drawing a Card from a Deck.
18. How to figure out if Something is a Mutually Exclusive Event.
19. How to Tell the Difference Between Dependent and Independent Events.
20. Probability: Dice Rolling.
21. How to Draw a Venn diagram.
22. How to Create an Euler Diagram.
23. 5 choose 3: how to solve combinations.
24. How to use the fundamental counting principle.
25. How to find expected value for a diskreetti satunnaismuuttuja.

Todennäköisyysopin johdanto: Definitions

• Axiomatic Probability.
• Benfordin laki
• What is a Binomial Experiment?
• Perusluvut ja perusluvun harhaluulo
• Brier-pisteet
• Kollektiivisesti tyhjentävä
• Mitä ovat kombinaatiot?
• Komplementaariset tapahtumat.
• Ehdollinen odotus
• Mitä on ehdollinen suhteellinen esiintymistiheys?
• Laskettava additiivisuus
• Tyhjä joukko
• Episteellinen todennäköisyys
• Tapahtuma-avaruudet.
• Mitä on kokeellinen todennäköisyys?
• Yhteensopivat todennäköisyysjakaumat.
• Rajoitusjakauma.
• Maximum Likelihood Estimation
• Memoryless Property.
• Monte Carlo Method.
• Monty Hall Problem
• What is a Mutually Exclusive Event?
• What is a Mutually Inclusive Events?
• Vastavuoroisesti riippumattomat ja pareittain riippumattomat.
• Mikä on kertolaskusääntö?
• Nashin tasapaino
• Ei-tyhjä joukko
• Normaalitodennäköisyys Harjoitusongelmia.
• Mikä on normaalitodennäköisyysdiagrammi?
• Objektiivinen todennäköisyys
• Mikä on odds ratio?
• Prediktiivinen analytiikka
• Mikä on todennäköisyysjakaumataulukko?
• Todennäköisyysmitta
• Mikä on todennäköisyysavaruus?
• Todennäköisyysvektorit
• Mitä ovat otosavaruudet?
• Stokastiset mallit.
• Mitä on subjektiivinen todennäköisyys?
• Mitä on teoreettinen todennäköisyys?
• Mitä on uurnamalli?

Laskurit.

• Online permutaatiolaskuri ja yhdistelmälaskuri.

Todennäköisyyskaavat / Todennäköisyyssäännöt

Yksi epämiellyttävimmistä asioista, joita opiskelijat eivät pidä kaavoista, on niiden puute todennäköisyydessä ja tilastotieteessä. On olemassa muutamia niittejä, mukaan lukien joitakin pakollisia merkintätapoja:

Todennäköisyysalue
0 ≤ P(A) ≤ 1
Tässä sanotaan, että jonkin tapahtuman todennäköisyys on jossakin nollan ja 100 %:n välissä (desimaalilukuna se on 0 ja 1). Tämä sääntö kannattaa muistaa, kun lasket yhteen tai kerrot tapahtumien todennäköisyyksiä. Jos vastauksesi on yli 100 %, se on vihje siitä, että olet saattanut tehdä jotain väärin.

Täydentävien tapahtumien sääntö
P(AC) + P(A) = 1
Täydentävät tapahtumat tapahtuvat silloin, kun on vain kaksi lopputulosta, kuten kolikon heittäminen. Kuution heittäminen sen selvittämiseksi, saisitko kuuden, on myös komplementaarinen tapahtuma; ainoat kaksi lopputulosta ovat kuuden saaminen (1/6 mahdollisuus) tai kuuden saamatta jättäminen (5/6 mahdollisuus). Molempien todennäköisyyksien summan on oltava 1.
Voi myös nähdä tämän kaavan kirjoitettuna näin:
p(A) + p(A’) = 1
joka voidaan järjestää algebrallisesti seuraavasti:
p(A’) = 1 – p(A).
Kaikki kolme kaavaa ovat ekvivalentteja: oppikirjan laatijasta ja opettajasta riippuu, mitä terminologiaa (A’ vai Ac) käytetään. Henkilökohtaisesti pidän enemmän A’:sta, jota kutsun ”ei A:ksi”. Todennäköisyys ”ei A” on mielestäni helpompi ymmärtää kuin ”komplementti” (joko tapahtuma tapahtuu tai se ei tapahdu).

Lisäyssääntö
P(A∪B) = P(A) + P(B) – P(A∩B)
jossa ∪ on unioni ja ∩ on leikkaus.
Mitä tämä tarkoittaa (suomeksi!) on, että todennäköisyys sille, että tapahtuma A TAI tapahtuma B tapahtuu (tai molemmat samaan aikaan) on:

• Todennäköisyys sille, että tapahtuma A tapahtuu yksinään,
• Plussatodennäköisyys sille, että tapahtuma B tapahtuu yksinään,
• Plussatodennäköisyys sille, että kumpikin tapahtuma tapahtuu samaan aikaan.

Jos sinulla on toisensa poissulkevia tapahtumia, niin P(A∩B) ei voi tapahtua (tapahtumat eivät voi tapahtua yhdessä), joten kaavasta tulee:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Disjointitapahtumat
Tapahtumat A ja B ovat disjointitapahtumia, jos:
P(A∩B) = 0
Tämähän on vain eräs toinen tapa sanoa, että tapahtumat sulkevat pois toisensa. Ne eivät voi tapahtua samaan aikaan.

Seuraava kaava on P((A∪B)c) tai vastaavasti ((A∪B)’). Englanniksi tämä sanoo ”not the union”. Ratkaistaksesi tämän, laske yhteenliittymä ja ota tulos pois 1:stä (koska todennäköisyyden, että tapahtumat tapahtuvat tai eivät tapahdu, on oltava yhtä suuri kuin 1).

Ehdollinen todennäköisyys
P(A|B) = P(A∩B) / P(B)
Symboli ”|” tarkoittaa ”edellyttäen, että”. Toisin sanoen todennäköisyys sille, että tapahtuma B tapahtuu, jos tapahtuma A tapahtuu. Esimerkkejä kaavan käytöstä löydät osoitteesta: Ehdollinen todennäköisyys.

Bayesin kaava
P(A|B) = P(B|A) – P(A) / P(B)
Bayesin teoreema on keino selvittää ehdollinen todennäköisyys, joskin se on hieman vivahteikkaampi. Lyhyesti sanottuna se antaa tapahtuman todellisen todennäköisyyden, kun otetaan huomioon tiedot testeistä. Esimerkiksi, mikä on todennäköisyys, että sinulla on syöpä, jos lääketieteellinen testisi on positiivinen (vastaus = paljon pienempi kuin luulet). Joitakin esimerkkejä, ks: Bayesin teoreeman esimerkkejä ja Posterioriset jakaumat / Posterioriset todennäköisyydet.

riippumattomat tapahtumat
Tapahtumat A ja B ovat riippumattomia, jos toinen niistä ei vaikuta toisen todennäköisyyteen. Tapahtumien sanotaan olevan riippumattomia myös, jos seuraava yhtälö pätee.
P(A∩B) = P(A) – P(B).
Tämä yhtälö on johdettu kertolaskusäännöstä, jonka mukaan P(A∩B) = P(A) * P(B|A). Koska tiedämme, että P(B|A) = P(B) riippumattomille tapahtumille, voimme korvata P(B):n P(B):llä P(B|A):lla, jolloin saamme kaavan.

Joitakin huomioita todennäköisyyssäännöistä

Tilastotieteessä on kyse sattumasta ja palloilusta, ei absoluuttisuudesta ja ”oikeasta vastauksesta”. Katsokaa vain mitä tahansa Gallupin gallup-kyselyä – he ovat harvoin yli 90-prosenttisen varmoja siitä, että heillä on ”oikea vastaus”. On olemassa tekniikoita, joita voit käyttää todennäköisyyksien laskemiseen (kuten kahden todennäköisyyden kertominen keskenään tai niiden laskeminen yhteen). Mutta lukuun ottamatta ehkä binomijakaumataulukkoa ja edellä mainittuja kaavoja (joita ei oikeassa elämässä käytetä kovinkaan paljon), ei oikeastaan ole olemassa muita todennäköisyyskaavoja, joita voisi helposti soveltaa. Sinun on palattava takaisin vanhaan peruskoulun perusasioihin, logiikkaan (muistathan sen… se oli siellä juuri ennen kuin sinulta alettiin testata logiikkaa standardoitujen testien avulla).

Todennäköisyyskaavojen kolme sääntöä:

1. Sääntöjä ei ole (no, hyvin vähän, paitsi yllä luetellut).
2. Käyttäkää logiikkaa, älkää yhtälöitä.
3. On monia, monia erilaisia tapoja päästä vastaukseen – joista yksikään ei oikeastaan käytä kaavoja.

Tänään saapui postilaatikkooni kysymys, joka käsittelee todennäköisyyksiä:

”Jos yrittäisit kerätä 6 baseball-korttia, jotka tulivat juustohöyläpakkauksissa, olettaen, että ne ovat jakautuneet tasaisesti, kuinka monta juustohöyläpakkausta odottaisit joutuvasi ostamaan, ennen kuin sinulla on käytössäsi kaikki 6 korttia?”

Vaihe 1 tämän ongelman ratkaisemisessa on sen tajuaminen, ettet voi katsoa vastausta taulukosta. Ratkaistaksesi sen sinun on ajateltava kuin lapsi.

Kortti nro 1:Olet taas 8-vuotias ja kävelet kauppaan, jossa sinulla on tarpeeksi rahaa ostaaksesi yhden pussillisen juustopuffeja. Toivot kerääväsi kaikki 5 baseball-korttia, mutta sinulla ei ole vielä yhtään. Mikä on todennäköisyys, että ostat pussin ja saat haluamasi kortin?

Vastaus on tietenkin 100 %. Osta ensimmäinen pussi, ja sinulla on 100% todennäköisyys, että siinä on kortti, jonka haluat.

Kortti nro 2: Nyt tilanne muuttuu hieman hankalammaksi. Palaat kauppaan hakemaan korttia#2. Mutta koska olet jo saanut kortin #1, Mickey Mantle. Et halua häntä uudestaan, mutta on 1/5 mahdollisuus, että saat hänet (ja siis 4/5 mahdollisuus, että et saa). Kuinka monta juustopussia sinun on ostettava saadaksesi kortin nro 2, muodostuu suhdelukuongelmaksi. Voit keksiä sen päässäsi, mutta jos haluat mallintaa sen matemaattisesti, sinun on asetettava yhtälö. Jos yksi pussi juustopuffeja antaa sinulle 80 %:n mahdollisuuden saada haluamasi kortti, kuinka monta pussia sinun täytyy ostaa saadaksesi 100 %:n mahdollisuuden?

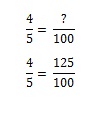
Saadaksesi 100 %:n sinun täytyy ostaa 1,25 pussia.

Kortti nro 3:Todennäköisyydet alkavat muuttua vaikeammiksi. Sinulla on 60 %:n mahdollisuus saada kolmas pesäpallokortti, ja sinun pitäisi ostaa 1,667 pussia saadaksesi tuon kolmannen kortin.

Kortti# 4:Kertoimet alkavat muuttua hieman synkemmiksi. Sinulla on 40 prosentin mahdollisuus saada neljäs baseball-kortti, ja sinun on ostettava 2,5 pussia saadaksesi tuon kolmannen kortin.

Kortti# 5:Kertoimet ovat sinua vastaan. Sinulla on 20 prosentin mahdollisuus saada viimeinen kortti, ja sinun on ostettava 5 pussia saadaksesi tuon kolmannen kortin.

Siten pussien kokonaismäärä, joka sinun on ostettava, on yhtä suuri kuin:
1 + 1,25 + 1,667 + 2,5 + 5
Mutta odota! (Ja tässä kohtaa pieni logiikka tulee mukaan). Et voi mennä kauppaan ja ostaa 1,25 pussia juustohöylää, joten sinun on pyöristettävä. Yhtälöstä tulee:
1 + 2 + 2 + 3 + 5 = 13 pussia.

Yksi tärkeä seikka kaavojen suhteen: muista, että mikään ei ole absoluuttista. Olen kohtuullisen varma siitä, että jos ostaisit 13 pussillista juustonaksuja ja olettaen, että kortit jakautuvat tasaisesti, saisit kaikki 5 korttia. Mutta… todennäköisyydessä on kyse sattumasta, ja voi olla vain huonoa tuuria saada sama kortti 10 kertaa peräkkäin (muistan, että minulle kävi niin lapsena). ”Huonolle tuurillesi” voi kuitenkin olla toinenkin selitys, ja se on se, että yritykset haluavat sinun ostavan mahdollisimman monta pussia, joten ne yrittävät saada todennäköisyydet toimimaan omaksi edukseen. Vaikka kortit olisivatkin jakautuneet tasaisesti, yhtiö voi lähettää pussit, joissa on kortit nro 1, nro 2 ja nro 3, yhteen kauppaan (ja siten houkutella sinut keräämään yli puolet korteista) ja pussit, joissa on kortit nro 4 ja nro 5, toiseen kauppaan.

Mitä muita tapoja keksit, joilla valmistajat voisivat kääntää todennäköisyydet edukseen?

Todennäköisyys, että ryhmä valitsee saman asian

Todennäköisyyskysymykset voidaan jakaa eri tyyppeihin. Kun sinua pyydetään löytämään todennäköisyys sille, että ryhmä valitsee saman asian, tarkastelet ryhmän satunnaisten jäsenten toimia (ryhmä voi olla niinkin pieni kuin komitea tai yhtä suuri kuin Yhdysvaltojen väestö).
Nämä todennäköisyyskysymykset antavat sinulle ryhmän ja pyytävät sinua laskemaan tapahtuman toteutumisen todennäköisyyden tietylle määrälle satunnaisia jäseniä tässä ryhmässä.

Todennäköisyys, että ryhmä valitsee saman asian : vaiheet

Esimerkkiongelma: Kirjamessuilla on 200 ihmistä. Heistä 159 ostaa vähintään yhden kirjan. Jos kysytään viideltä satunnaisesti ovesta ulos tulevalta ihmiseltä, mikä on todennäköisyys, että he kaikki ovat ostaneet vähintään yhden kirjan?

Millä todennäköisyydellä ryhmä ostaa vähintään yhden kirjan?

Vaihe 1: Muunna kysymyksen tiedot murtoluvuksi. Esimerkiksi lause ”159 ihmistä 200:sta” voidaan muuntaa muotoon: 159/200.

Vaihe 2: Kerro murtoluku itsellään. Toista tämä kuinka monelle satunnaiskohteelle (eli ihmiselle) tahansa. Esimerkissämme on 5 tutkittua henkilöä, joten haluamme:

159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0.3176
Siten saadaan selville todennäköisyys sille, että ryhmä valitsee saman asian!

Vinkki: Voi olla helpompaa muuntaa murtoluku desimaaliluvuksi ennen kertomista. Tässä tapauksessa 159/200 = 0,795.

Katso YouTube-kanavamme, josta löydät lisää apua ja vinkkejä tilastoihin! Meillä on videoita yleisimpiin ongelmiin, joihin todennäköisesti törmäät. Lisäksi videoita Excelin käytöstä tilastotieteessä > kaikenlaiseen perustason pylväsdiagrammeista monimutkaisten data-analyysiongelmien ratkaisemiseen.

——————————————————————————

Tarvitsetko apua kotitehtävän tai kokeen kysymyksen kanssa? Chegg Studyn avulla saat kysymyksiisi vaiheittaiset ratkaisut alan asiantuntijalta. Ensimmäiset 30 minuuttia Chegg-opettajan kanssa ovat ilmaisia!