Interpréter les coefficients de régression linéaire

Apprendre à interpréter correctement les résultats de la régression linéaire – y compris les cas avec des transformations de variables
De nos jours, il existe une pléthore d’algorithmes d’apprentissage automatique que nous pouvons essayer pour trouver le meilleur ajustement pour notre problème particulier. Certains de ces algorithmes ont une interprétation claire, d’autres fonctionnent comme une boîte noire et nous pouvons utiliser des approches telles que LIME ou SHAP pour dériver certaines interprétations.
Dans cet article, je voudrais me concentrer sur l’interprétation des coefficients du modèle de régression le plus basique, à savoir la régression linéaire, y compris les situations où les variables dépendantes/indépendantes ont été transformées (dans ce cas, je parle de la transformation logarithmique).
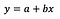
Je suppose que le lecteur est familier avec la régression linéaire (si ce n’est pas le cas, il y a beaucoup de bons articles et de posts Medium), donc je vais me concentrer uniquement sur l’interprétation des coefficients.
La formule de base de la régression linéaire peut être vue ci-dessus (j’ai omis les résidus à dessein, pour garder les choses simples et au point). Dans la formule, y désigne la variable dépendante et x est la variable indépendante. Pour simplifier, supposons qu’il s’agit d’une régression univariée, mais les principes sont évidemment valables pour le cas multivarié également.
Pour mettre cela en perspective, disons qu’après avoir ajusté le modèle, nous obtenons :
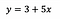
Intercept (a)
Je vais décomposer l’interprétation de l’intercept en deux cas :
- x est continu et centré (en soustrayant la moyenne de x à chaque observation, la moyenne de x transformée devient 0) – la moyenne y est 3 lorsque x est égal à la moyenne de l’échantillon
- x est continu, mais non centrée – la moyenne y est de 3 lorsque x = 0
- x est catégorique – la moyenne y est de 3 lorsque x = 0 (indiquant cette fois une catégorie, plus sur ce point ci-dessous)
Coefficient (b)
- x est une variable continue
Interprétation : une augmentation unitaire de x entraîne une augmentation de la moyenne y de 5 unités, toutes les autres variables restant constantes.
- x est une variable catégorielle
Cela demande un peu plus d’explications. Disons que x décrit le sexe et peut prendre les valeurs (‘male’, ‘female’). Maintenant, convertissons-le en une variable muette qui prend les valeurs 0 pour les hommes et 1 pour les femmes.
Interprétation : le y moyen est plus élevé de 5 unités pour les femmes que pour les hommes, toutes les autres variables restant constantes.
Modèle à niveau logarithmique
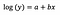
Typiquement, nous utilisons la transformation logarithmique pour rapprocher les données aberrantes d’une distribution positivement asymétrique de la majeure partie des données, afin de rendre la variable normalement distribuée. Dans le cas de la régression linéaire, un avantage supplémentaire de l’utilisation de la transformation logarithmique est l’interprétabilité.
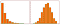
Comme précédemment, disons que la formule ci-dessous présente les coefficients du modèle ajusté.
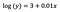
Intercept (a)
L’interprétation est similaire à celle du cas vanille (niveau), cependant, nous devons prendre l’exposant de l’intercept pour l’interprétation exp(3) = 20,09. La différence est que cette valeur représente la moyenne géométrique de y (par opposition à la moyenne arithmétique dans le cas du modèle à niveau).
Coefficient (b)
Les principes sont à nouveau similaires au modèle à niveau lorsqu’il s’agit d’interpréter des variables catégorielles/numériques. Analogiquement à l’ordonnée à l’origine, nous devons prendre l’exposant du coefficient : exp(b) = exp(0,01) = 1,01. Cela signifie qu’une augmentation unitaire de x entraîne une augmentation de 1% de la moyenne (géométrique) y, toutes les autres variables restant constantes.
Deux choses qui méritent d’être mentionnées ici :
- Il existe une règle empirique lorsqu’il s’agit d’interpréter les coefficients d’un tel modèle. Si abs(b) < 0,15, il est tout à fait sûr de dire que lorsque b = 0,1, nous observerons une augmentation de 10% de y pour un changement d’unité de x. Pour les coefficients avec une valeur absolue plus grande, il est recommandé de calculer l’exposant.
- Lorsqu’on a affaire à des variables en fourchette (comme un pourcentage), il est plus pratique pour l’interprétation de multiplier d’abord la variable par 100, puis d’ajuster le modèle. De cette façon, l’interprétation est plus intuitive, car nous augmentons la variable de 1 point de pourcentage au lieu de 100 points de pourcentage (de 0 à 1 immédiatement).
Modèle logarithmique à deux niveaux
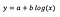
Supposons qu’après avoir ajusté le modèle, nous obtenions :

L’interprétation de l’intercept est la même que dans le cas du modèle à niveau.
Pour le coefficient b – une augmentation de 1% de x entraîne une augmentation approximative de y moyen de b/100 (0,05 dans ce cas), toutes les autres variables restant constantes. Pour obtenir le montant exact, il faudrait prendre b× log(1,01), ce qui donne dans ce cas 0,0498.
Modèle log-log
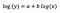
Supposons qu’après avoir ajusté le modèle, nous obtenions :
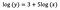
Une fois encore, je me concentre sur l’interprétation de b. Une augmentation de x de 1% entraîne une augmentation de 5% de la moyenne (géométrique) y, toutes les autres variables restant constantes. Pour obtenir le montant exact, nous devons prendre
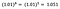
ce qui représente ~5,1%.
Conclusions
J’espère que cet article vous a donné un aperçu de la façon d’interpréter les coefficients de régression linéaire, y compris les cas où certaines des variables ont été log-transformées. Comme toujours, tout commentaire constructif est le bienvenu. Vous pouvez me joindre sur Twitter ou dans les commentaires.




