Introduction aux probabilités : Articles et vidéos avec solutions !

admin 0 Comments Articles

Introduction aux probabilités : Articles et vidéos avec solutions !

Lancer de dés, trouver une place de parking, gagner aux cartes ; Ce ne sont que quelques situations où vous pourriez vouloir trouver les probabilités qu’un événement se produise. Si vous voulez savoir comment trouver la probabilité, vous devez d’abord déterminer le type de question que vous vous posez. Par exemple, la façon de trouver les probabilités qu’un événement se produise est différente de celle de trouver les probabilités que les membres d’un groupe choisissent la même chose.

Certaines probabilités sont faciles à identifier, comme trouver les probabilités de lancer un dé ou de piocher dans un jeu de cartes.

Les questions qui impliquent le théorème binomial sont également faciles à identifier. Dans ces types d’expériences, les seules issues possibles d’un événement sont « Succès » ou « Échec » : comme oui/non, tête/queue ou noir/blanc.

D’autres types de questions que vous pourriez rencontrer impliquent des personnes, comme :

• Sélectionner une personne dans un groupe ou un comité.
• Probabilité qu’un groupe choisisse la même chose.

Événements

Vous voulez trouver la probabilité qu’un événement simple se produise ? Comme la pluie, ou trouver une place de parking en ville ? Voir :
Probabilité qu’un événement simple se produise.
En revanche, si vous voulez exactement le contraire, voir :
Comment trouver la probabilité qu’un événement NE se produise PAS.

Votre question porte-t-elle sur la survenance d’un événement compte tenu d’un autre événement ? Comme les chances de trouver une place de parking, étant donné que c’est jour de match, ou de trouver un certain jouet populaire le vendredi noir ? Si c’est le cas, vérifiez :

• Les chances d’un événement, étant donné un autre événement.
• Deux événements se produisant ensemble.

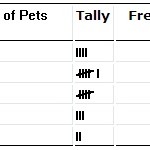
Un tableau de distribution de fréquences.

Distributions de fréquences

Avez-vous une distribution de fréquences avec laquelle travailler ? Ou êtes-vous capable de faire un tableau de distribution de fréquence avec vos données données ? Par exemple, vous avez x nombre d’articles avec un certain caractère. Distribution de fréquence des probabilités.

Introduction aux probabilités : articles et vidéos pratiques.

1. Permutations et combinaisons : Comment résoudre les problèmes
2. Problèmes de probabilités : Résolvez-les de manière simple !
3. Probabilité de a et b.
4. Règle de probabilité totale.
5. Problèmes de théorème de Bayes : Étapes de solution faciles.
6. Probabilité antérieure (y compris non informative et conjuguée).
7. Comment faire une distribution de probabilité à partir de données.
8. Comment trouver la probabilité de choisir une personne dans un groupe ou un comité.
9. Comment trouver la probabilité qu’un événement ne se produise PAS.
10. Distribution de fréquence des probabilités.
11. Comment trouver la probabilité qu’un événement simple se produise.
12. Événement aléatoire : Probabilité étant donné un pourcentage.
13. Comment trouver la probabilité que les membres d’un groupe choisissent la même chose.
14. Comment trouver la probabilité que deux événements dépendants se produisent ensemble.
15. Comment trouver la probabilité qu’un événement se produise, étant donné un autre événement.
16. Comment utiliser un arbre de probabilité (arbre de décision) pour calculer les probabilités.
17. Comment trouver la probabilité de tirer une carte d’un jeu.
18. Comment déterminer si quelque chose est un événement mutuellement exclusif.
19. Comment faire la différence entre des événements dépendants et indépendants.
20. Probabilité : Lancer de dés.
21. Comment dessiner un diagramme de Venn.
22. Comment créer un diagramme d’Euler.
23. 5 choisir 3 : comment résoudre les combinaisons.
24. Comment utiliser le principe fondamental du comptage.
25. Comment trouver la valeur attendue pour une variable aléatoire discrète.

Introduction aux probabilités : Définitions

• Probabilité axiomatique.
• La loi de Benford
• Qu’est-ce qu’une expérience binomiale ?
• Taux de base et sophisme du taux de base
• Scores de Brier
• Exhaustivité collective
• Que sont les combinaisons ?
• Événements complémentaires.
• Espérance conditionnelle
• Qu’est-ce que la fréquence relative conditionnelle ?
• Additivité dénombrable
• Ensemble vide
• Probabilité épistémique
• Espaces événementiels.
• Qu’est-ce que la probabilité expérimentale ?
• Distributions de probabilités conjointes.
• Distribution limite.
• Estimation du maximum de vraisemblance
• Propriété sans mémoire.
• Méthode de Monte Carlo.
• Problème de Monty Hall
• Qu’est-ce qu’un événement mutuellement exclusif ?
• Qu’est-ce qu’un événement mutuellement inclusif ?
• Mutuellement indépendants et indépendants par paires.
• Qu’est-ce que la règle de multiplication ?
• Equilibre de Nash
• Ensemble non vide
• Problèmes pratiques de probabilité normale.
• Qu’est-ce qu’un tracé de probabilité normale ?
• Probabilité objective
• Qu’est-ce que le rapport de cotes ?
• Analyse prédictive
• Qu’est-ce qu’un tableau de distribution des probabilités ?
• Mesure de probabilité
• Qu’est-ce qu’un espace de probabilité ?
• Vecteurs de probabilité
• Que sont les espaces échantillons ?
• Modèles stochastiques.
• Qu’est-ce qu’une probabilité subjective ?
• Qu’est-ce que la probabilité théorique ?
• Qu’est-ce qu’un modèle d’urne ?

Calculateurs.

• Calculateur de permutations et calculateur de combinaisons en ligne.

Formules de probabilité / Règles de probabilité

L’une des choses les plus gênantes que les étudiants n’aiment pas dans les formules est leur absence en probabilité et en statistique. Il y a quelques agrafes, y compris certaines notations à connaître absolument :

Etendue de probabilité
0 ≤ P(A) ≤ 1
Ceci stipule que la probabilité d’un événement est quelque part entre zéro et 100% (en décimal, c’est 0 et 1). Vous voudrez vous souvenir de cette règle lorsque vous ajouterez ou multiplierez les probabilités d’événements. Si votre réponse est supérieure à 100%, c’est un indice que vous avez peut-être fait quelque chose de mal.

Règle des événements complémentaires
P(AC) + P(A) = 1
Les événements complémentaires se produisent lorsqu’il n’y a que deux issues, comme le lancer d’une pièce de monnaie. Lancer un dé pour voir si vous obtiendrez six est également complémentaire ; les deux seules issues sont d’obtenir un six (une chance sur six) ou de ne pas obtenir un six (une chance sur cinq). La somme des deux probabilités doit être égale à 1.
Vous pouvez aussi voir cette formule s’écrire comme ceci :
p(A) + p(A’) = 1
qui peut être réarrangé algébriquement pour donner :
p(A’) = 1 – p(A).
Ces trois formules sont équivalentes : la terminologie (A’ ou Ac) utilisée est laissée à l’appréciation de l’auteur du manuel et de l’enseignant. Personnellement, je préfère A’, que j’appelle « pas A ». La probabilité de « pas A », je pense, est plus facile à comprendre que « le complément » (soit un événement se produit, soit il ne se produit pas).

Règle d’addition
P(A∪B) = P(A) + P(B) – P(A∩B)
où ∪ est l’union et ∩ l’intersection.
Ce que cela dit (en anglais !) est que la probabilité que l’événement A OU l’événement B se produise (ou les deux en même temps) est :

• La probabilité que l’événement A se produise seul,
• Plus la probabilité que l’événement B se produise seul,
• Plus la probabilité que les deux événements se produisent en même temps.

Si vous avez des événements qui s’excluent mutuellement, alors P(A∩B) ne peut pas se produire (les événements ne peuvent pas se produire ensemble), donc la formule devient :
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Événements disjoints
Les événements A et B sont disjoints si :
P(A∩B) = 0
C’est juste une autre façon de dire que les événements sont mutuellement exclusifs. Ils ne peuvent pas se produire en même temps.

Une formule connexe est P((A∪B)c) ou, de manière équivalente ((A∪B)’). En anglais, cela veut dire « not the union ». Pour résoudre cela, il faut calculer l’union et retirer le résultat de 1 (car la probabilité que les événements se produisent ou ne se produisent pas doit s’additionner à 1).

Probabilité conditionnelle
P(A|B) = P(A∩B) / P(B)
Le symbole « | » signifie « étant donné que ». En d’autres termes, la probabilité que l’événement B se produise, étant donné que l’événement A se produit. Pour des exemples d’utilisation de la formule, voir : probabilité conditionnelle.

Formule de Bayes
P(A|B) = P(B|A) – P(A) / P(B)
Le théorème de Bayes est un moyen de calculer la probabilité conditionnelle, bien qu’il soit légèrement plus nuancé. En un mot, il vous donne la probabilité réelle d’un événement compte tenu des informations sur les tests. Par exemple, quelle est la probabilité que vous ayez un cancer si votre test médical est positif (réponse = beaucoup plus faible que vous ne le pensez). Pour quelques exemples, voir : Exemples du théorème de Bayes et Distributions postérieures / Probabilités postérieures.

Événements indépendants
Les événements A et B sont indépendants si l’un d’eux n’affecte pas la probabilité de l’autre. On dit aussi que les événements sont indépendants si l’équation suivante est vraie.
P(A∩B) = P(A) – P(B).
Cette équation est dérivée de la règle de multiplication, qui dit que P(A∩B) = P(A) * P(B|A). Comme nous savons que P(B|A) = P(B) pour des événements indépendants, nous pouvons substituer P(B|A) à P(B), ce qui nous donne la formule.

Quelques notes sur les règles de probabilité

Les statistiques sont une question de chance et de ballparking, pas d’absolus et de « bonne réponse ». Il suffit de regarder n’importe quel sondage Gallup – ils sont rarement plus de 90% à penser qu’ils ont la « bonne réponse ». Il existe des techniques que vous pouvez utiliser pour calculer les probabilités (comme multiplier deux probabilités ensemble ou les additionner). Cependant, à part peut-être le tableau de distribution binomiale et les formules ci-dessus (qui, dans la vie réelle, ne sont pas tellement utilisées), il n’existe pas vraiment de formules de probabilité faciles à appliquer. Vous devez revenir à ce vieil aliment de base de l’école primaire, la logique (vous vous en souvenez… c’était là juste avant qu’ils ne commencent à tester standardisé la logique hors de vous).

Les trois règles des formules de probabilité :

1. Il n’y a pas de règles (enfin, très peu, sauf celles énumérées ci-dessus).
2. Utilisez la logique, pas les équations.
3. Il y a beaucoup, beaucoup de façons différentes d’arriver à la réponse – aucune n’utilise vraiment les formules.

Voici une question qui est arrivée dans ma boîte de réception ce matin et qui aborde les probabilités :

« Si vous essayiez de collecter 6 cartes de baseball qui sont venues dans des paquets de soufflés au fromage, en supposant qu’elles sont distribuées uniformément, combien de paquets de soufflés au fromage vous attendriez-vous à acheter avant d’avoir les 6 cartes ? »

L’étape 1 pour résoudre ce problème est de réaliser que vous ne pouvez pas chercher la réponse dans un tableau. Pour le résoudre, vous devez penser comme un enfant.

Carte# 1:Vous avez à nouveau 8 ans et entrez dans un magasin avec assez d’argent pour acheter un sac de soufflés au fromage. Vous espérez collectionner les 5 cartes de baseball mais vous n’en avez pas encore. Quelles sont les chances que vous achetiez un sac et que vous obteniez une carte que vous voulez ?

La réponse, bien sûr, est 100%. Achetez votre premier sac, et vous avez 100% de chances qu’il contienne une carte que vous voulez.

Carte n° 2 : Maintenant, ça devient un peu plus délicat. Vous retournez au magasin pour obtenir la carte#2. Mais comme vous avez déjà eu la carte n°1, Mickey Mantle. Vous ne voulez plus de lui, mais il y a 1/5 de chance que vous l’ayez (et donc 4/5 de chance que vous ne l’ayez pas). Le nombre de sacs de soufflés au fromage que vous devrez acheter pour obtenir la carte n° 2 devient un problème de ratio. Vous pouvez le calculer dans votre tête, mais si vous voulez le modéliser mathématiquement, vous devez établir l’équation. Si un sac de soufflés au fromage vous donne 80 % de chances d’obtenir la carte que vous voulez, combien de sacs devez-vous acheter pour avoir 100 % de chances ?

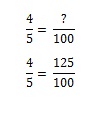
Pour obtenir 100 %, vous devriez acheter 1,25 sac.

Carte n° 3 : Les chances commencent à devenir plus difficiles. Vous avez 60% de chances d’obtenir la troisième carte de baseball, et vous devrez acheter 1,667 sacs pour obtenir cette troisième carte.

Carte# 4:Les chances commencent à être un peu lugubres. Vous avez 40% de chances d’obtenir la quatrième carte de baseball, et vous devrez acheter 2,5 sacs pour obtenir cette troisième carte.

Carte# 5:Les chances sont contre vous. Vous avez 20 % de chances d’obtenir la dernière carte, et vous devrez acheter 5 sacs pour obtenir cette troisième carte.

Donc le nombre total de sacs que vous devrez acheter est égal à :
1 + 1,25 + 1,667 + 2,5 + 5
Mais attendez ! (Et c’est ici qu’un peu de logique entre en jeu). Vous ne pouvez pas aller dans un magasin et acheter 1,25 sacs de soufflés au fromage, vous devrez donc arrondir. L’équation devient :
1 + 2 + 2 + 3 + 5 = 13 sacs.

Un point important pour les formules : n’oubliez pas que rien n’est absolu. Je suis raisonnablement confiant que si vous achetez 13 sacs de soufflés au fromage et en supposant que les cartes sont distribuées uniformément, que vous obtiendrez les 5 cartes. Mais… les probabilités sont liées au hasard, et vous pourriez n’avoir que de la malchance d’obtenir la même carte 10 fois de suite (je me souviens que cela m’est arrivé quand j’étais enfant). Mais il peut y avoir une autre explication à votre « malchance », et c’est que les entreprises veulent que vous achetiez autant de sacs que possible, et elles essaieront donc de faire tourner les chances en leur faveur. Même si les cartes sont distribuées de manière égale, l’entreprise pourrait expédier des sacs contenant les cartes #1, #2 et #3 à un magasin (vous attirant ainsi en vous faisant collectionner plus de la moitié des cartes) et #4 et #5 à un autre magasin.

Quelles autres façons pensez-vous que les fabricants pourraient faire tourner les chances en leur faveur ?

Probabilité qu’un groupe choisisse la même chose

Les questions de probabilité peuvent être décomposées en différents types. Lorsqu’on vous demande de trouver la probabilité qu’un groupe choisisse la même chose, vous considérez les actions des membres aléatoires d’un groupe (il peut être aussi petit qu’un comité ou aussi grand que la population des États-Unis).
Ces questions de probabilité vous donnent un groupe, et vous demandent de calculer la probabilité qu’un événement se produise pour un certain nombre de membres aléatoires au sein de ce groupe.

Probabilité qu’un groupe choisisse la même chose : étapes

Problème type : Il y a 200 personnes à un salon du livre. 159 d’entre elles vont acheter au moins un livre. Si vous interrogez 5 personnes au hasard qui sortent de la porte, quelle est la probabilité qu’elles aient toutes acheté au moins un livre ?

Quelle est la probabilité qu’un groupe achète au moins un livre ?

Étape 1 : Convertissez les données de la question en fraction. Par exemple, la phrase « 159 personnes sur 200 » peut être convertie en : 159/200.

Étape 2 : Multiplier la fraction par elle-même. Répétez l’opération pour le nombre d’éléments aléatoires (c’est-à-dire de personnes) choisis. Dans notre exemple, nous avons 5 personnes interrogées, nous voulons donc :

159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
C’est ainsi que l’on trouve la probabilité qu’un groupe choisisse la même chose !

Conseil : Il peut être plus facile de convertir la fraction en décimal avant de multiplier. Dans ce cas, 159/200 = 0,795.

Consultez notre chaîne YouTube pour plus d’aide et de conseils sur les statistiques ! Nous avons des vidéos pour les problèmes les plus courants que vous êtes susceptibles de rencontrer. Plus des vidéos pour utiliser Excel dans les stats > tout, de la réalisation de graphiques à barres de base à la résolution de problèmes complexes d’analyse de données.

——————————————————————————

Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !