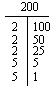A számok prímszámukban
Minden egész számot prímszámnak vagy összetettnek minősítünk, kivéve a nullát és az egyest, amelyek speciális esetek. Nézzük meg, mi a különbség a prímszámok és az összetett számok között. A prímszámoknak pontosan két tényezője van, egy és maga a szám. Ha ismered az oszthatósági szabályokat (amelyekről a következő részben lesz szó), akkor az 1-100 közötti prímszámok meghatározása viszonylag egyszerű feladat. Íme a prímszámok 25-ig:
2, 3, 5, 7, 11, 13, 17, 19, 23
Nincs minta az összes létező prímszám megtalálására, bár a matematikusok találtak már közel nyolcmillió számjegyű prímszámot. Ez az egyik megmaradt nagy matematikai rejtély a matematikusok számára.
Az összetett számoknak kettőnél több tényezőjük van, de nem végtelen számú. Minden páros szám (a kettes szám kivételével) összetett, mivel mindegyik osztható kettővel.
A nulla nem prím és nem összetett szám. Mivel bármely szám szorozva nullával egyenlő nullával, a nulla szorzatának végtelen számú tényezője van. Egy összetett számnak véges számú tényezővel kell rendelkeznie.
Az egyes szintén nem prím és nem összetett. Az egyes szorzatát csak úgy kaphatjuk meg, ha megszorozzuk 1 x 1. A duplikált tényezőket azonban csak egyszer számoljuk, így az egyesnek csak egy tényezője van. (Egy prímszámnak pontosan két faktora van, tehát az egyes nem lehet prímszám.)
Egy tipikus tesztkérdésben meg kell határoznod, hogy egy listából melyik szám prímszám (vagy összetett, vagy egyik sem).
Próbáld ki ezt:
Kérdés
Az alábbiak közül melyik prímszám?
- 33
- 45
- 41
- 51
Válasz
A helyes válasz a C. A 41 prímszám, a többi szám összetett. Légy óvatos az 51-gyel – 3 x 17-ből származik.
Cool szabályok
A feloszthatósági szabályok olyan eszközök, amelyek segítenek abban, hogy kevesebb osztást végezzünk. Az oszthatósági szabályok segítenek meghatározni, hogy egy szám prím vagy összetett-e, valamint segítenek az összetett számokat prímtényezőikre bontani, amivel a következőkben foglalkozunk.
Az oszthatósági szabályok olyan rövidítések, amelyek megmondják, hogy egy szám osztható-e egy másik számmal. A szabályok lefedik a 2-10-es számokkal való osztást, és lehetővé teszik a számok ellenőrzését 100-ig. Kattints a számokra a táblázatban.
| Eloszthatósági szabályok | |||
|---|---|---|---|
| 2 | 3 | 4 | |
| 5 | 6 | 6 | 7 |
| 8 | 9 | 10 | |
Kérdés
Az alábbi számok közül melyik nem osztható 3-mal?
- 4,873
- 7,521
- 12,642
- 25,308
Válasz
A helyes válasz: A. A feladat megoldásának gyors módja az oszthatósági szabály alkalmazása; add össze az egyes számok számjegyeit, keresve azt, amelyik nem háromszorosa. A lassú módszer az lenne, ha minden egyes osztásfeladatot elvégeznénk – ez a módszer még számológépen is hosszabb időt vesz igénybe!
Prímtényezős szorzás: T-k és fa
Ez egy másik téma, amire talán már a középiskola óta nem gondoltál. Az aritmetika alaptétele kimondja, hogy minden összetett szám felbontható prímszámok egyedi szorzatára.
A prímtényezős faktorizálás az a folyamat, amely egy adott összetett szám prímszámterméket talál. A prímtényezős számképzés önmagában is hasznos, de számos alkalmazási területe a törtekkel kapcsolatos, amelyekkel a későbbiekben foglalkozunk.
Egy szám prímtényezőjét fejben is meg tudod találni. A 12 például 2 x 2 x 3 vagy 22 x 3. (A prímtényezőket gyakran exponensekkel ábrázolják.)
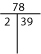
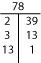
Ha gondolatban nem találod meg a prímtényezőket, próbáld ki a Factor-T-t vagy a Factor Tree-t.
Értekezés
- A prímszámoknak pontosan két tényezőjük van, egy és önmaga.
- Az összetett számoknak kettőnél több tényezőjük van, de nem végtelen számú.
- A nulla és az egy nem prím és nem összetett.
- Az oszthatósági szabályok olyan rövidítések, amelyek segíthetnek egy szám tényezőinek meghatározásában.
- Minden összetett szám felírható prímszámok egyedi szorzataként, amit a szám prímfaktorizációjának nevezünk.
- A prímfaktorizáció megtalálásának két praktikus módszere a T-faktor és a faktorfa.