Valószínűség Bevezetés: Cikkek és videók megoldásokkal!
 Kockadobás, parkolóhely megtalálása, kártyanyeremény; Ez csak néhány olyan helyzet, amikor egy esemény bekövetkezésének esélyét szeretnénk megtudni. Ha tudni akarod, hogyan találd meg a valószínűséget, először is ki kell találnod, hogy milyen kérdésed van. Például az, hogy hogyan találod meg egy esemény bekövetkezésének az esélyét, különbözik attól, hogy megkeresed annak az esélyét, hogy a csoport tagjai ugyanazt a dolgot választják.
Kockadobás, parkolóhely megtalálása, kártyanyeremény; Ez csak néhány olyan helyzet, amikor egy esemény bekövetkezésének esélyét szeretnénk megtudni. Ha tudni akarod, hogyan találd meg a valószínűséget, először is ki kell találnod, hogy milyen kérdésed van. Például az, hogy hogyan találod meg egy esemény bekövetkezésének az esélyét, különbözik attól, hogy megkeresed annak az esélyét, hogy a csoport tagjai ugyanazt a dolgot választják.
Egyes valószínűségeket könnyű meghatározni, mint például a kockadobás vagy a kártyapakliból való választás valószínűségének megtalálása.
A binomiális tételt tartalmazó kérdések szintén könnyen azonosíthatók. Az ilyen típusú kísérletekben egy esemény egyetlen lehetséges kimenetele a “Siker” vagy a “Kudarc”: például igen/nem, fej/farok vagy fekete/fehér.
A többi kérdéstípus, amellyel találkozhatsz, emberekkel kapcsolatos, például:
- Egy személy kiválasztása egy csoportból vagy bizottságból.
- Az azonos dolgot választó csoport valószínűsége.
Események
Egy egyszerű esemény bekövetkezésének valószínűségét szeretnéd megtalálni? Például hogy esik az eső, vagy hogy találsz egy parkolóhelyet a belvárosban? Lásd:
Egy egyszerű esemény bekövetkezésének valószínűsége.
Ha viszont pont az ellenkezőjét akarod, lásd:
Hogyan derítsük ki egy esemény NEM bekövetkezésének valószínűségét.
A kérdésed egy esemény bekövetkezésére vonatkozik egy másik esemény bekövetkezése esetén? Mint például annak az esélye, hogy találsz egy parkolóhelyet, tekintve, hogy játéknap van, vagy hogy találsz egy bizonyos népszerű játékot a fekete pénteken? Ha igen, akkor nézd meg:
- Egy esemény esélye, egy másik eseményt figyelembe véve.
- Két esemény együttes előfordulása.
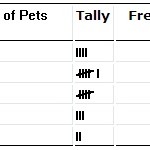
Egy gyakorisági eloszlási táblázat.
Sokasági eloszlások
Sokasági eloszlással kell dolgoznia? Vagy tudsz gyakorisági eloszlási táblázatot készíteni a megadott adatokból? Például van x darab bizonyos tulajdonságú tételed. Valószínűségi gyakorisági eloszlás.
Bevezetés a valószínűségszámításba: oktatócikkek és videók.
- Permutációk és kombinációk: How to Solve Problems
- Probability Problems:
- A és b valószínűsége.
- Teljes valószínűségi szabály.
- Bayes tétel feladatai: Easy Solution Steps.
- Prior Probability (including Uninformative and Conjugate).
- How to Make a Probability Distribution from data.
- How to find the Probability of Selecting a Person from a Group or Committee.
- Hogyan találjuk meg egy esemény NEM bekövetkezésének valószínűségét.
- Valószínűségi gyakorisági eloszlás.
- Hogyan találjuk meg egy egyszerű esemény bekövetkezésének valószínűségét.
- Véletlen esemény: Valószínűség adott százalékban.
- Hogyan találjuk meg annak valószínűségét, hogy a csoport tagjai ugyanazt a dolgot választják.
- Hogyan találjuk meg két függő esemény együttes bekövetkezésének valószínűségét.
- Hogyan találjuk meg egy esemény bekövetkezésének valószínűségét egy másik esemény esetén.
- Hogyan használjunk valószínűségi fát (döntési fát) az esélyek kiszámításához.
- Hogyan találjuk meg egy kártya pakliból való kihúzásának valószínűségét.
- Hogyan találjuk meg, hogy valami kölcsönösen kizáró esemény-e.
- Hogyan különböztessük meg a függő és független eseményeket.
- Probability: Dice Rolling.
- How to Draw a Venn diagram.
- How to Create an Euler Diagram.
- 5 choose 3: how to solve combinations.
- How to use the fundamental counting principle.
- How to find expected value for a discrete random variable.
Introduction to Probability: Definíciók
- Axiomatikus valószínűség.
- Benford törvénye
- Mi a binomiális kísérlet?
- A bázisráták és a bázisráta tévedés
- Brier pontszámok
- Kollektív kimerítő
- Mi a kombinációk?
- Kiegészítő események.
- Feltételes várakozás
- Mi a feltételes relatív gyakoriság?
- Megszámlálható additivitás
- Üres halmaz
- Episztemikus valószínűség
- Eseményterek.
- Mi a kísérleti valószínűség?
- Közös valószínűségi eloszlások.
- Határeloszlás.
- Maximum Likelihood becslés
- Memóriamentes tulajdonság.
- Monte Carlo módszer.
- Monty Hall probléma
- Mi az egymást kizáró esemény?
- Mi az egymást kizáró esemény?
- Kölcsönösen független és párosan független.
- Mi a szorzási szabály?
- Nash-egyensúly
- Nem üres halmaz
- Normál valószínűségi gyakorlati feladatok.
- Mi a normál valószínűségi ábra?
- Objektív valószínűség
- Mi az esélyhányados?
- Prediktív analitika
- Mi a valószínűségi eloszlási táblázat?
- Valószínűségi mérték
- Mi a valószínűségi tér?
- Valószínűségi vektorok
- Mik a mintaterek?
- Sztochasztikus modellek.
- Mi a szubjektív valószínűség?
- Mi az elméleti valószínűség?
- Mi az urnamodell?
Kalkulátorok.
- Online permutációs és kombinációs kalkulátor.
Valószínűségi képletek / valószínűségi szabályok
A valószínűségszámításban és a statisztikában az egyik legkellemetlenebb dolog, amit a diákok nem szeretnek a képletekkel kapcsolatban. Van néhány kapocs, köztük néhány kötelezően megismerendő jelölés:
Valószínűségi tartomány
0 ≤ P(A) ≤ 1
Ez azt mondja ki, hogy egy esemény valószínűsége valahol nulla és 100% között van (tizedesjegyként ez 0 és 1). Ezt a szabályt érdemes megjegyezni, amikor események valószínűségeit összeadod vagy megszorozod. Ha a válaszod 100% fölött van, az arra utal, hogy valamit rosszul csináltál.
A komplementer események szabálya
P(AC) + P(A) = 1
A komplementer események akkor következnek be, amikor csak két kimenetel van, például amikor feldobunk egy érmét. A kockadobás, hogy megtudjuk, kapunk-e hatost, szintén komplementer esemény; az egyetlen két kimenetel az, hogy hatost kapunk (1/6 esély) vagy nem kapunk hatost (5/6 esély). A két valószínűségnek össze kell adódnia 1-re.
Láthatjuk ezt a képletet így is leírva:
p(A) + p(A’) = 1
mely algebrailag átrendezve így hangzik:
p(A’) = 1 – p(A).
Mindhárom képlet egyenértékű: hogy melyik terminológiát (A’ vagy Ac) használjuk, az a tankönyv szerzőjétől és tanárától függ. Én személy szerint az A’-t részesítem előnyben, amit én “nem A”-nak nevezek. A “nem A” valószínűsége szerintem könnyebben érthető, mint a “komplementer” (vagy megtörténik egy esemény, vagy nem történik meg).
Adódási szabály
P(A∪B) = P(A) + P(B) – P(A∩B)
ahol ∪ az unió és ∩ a metszet.
Mit mond ez (magyarul!), hogy az A esemény VAGY a B esemény bekövetkezésének (vagy mindkettő egyidejű bekövetkezésének) valószínűsége:
- Az A esemény önmagában való bekövetkezésének valószínűsége,
- Plusz a B esemény önmagában való bekövetkezésének valószínűsége,
- Plusz a két esemény egyidejű bekövetkezésének valószínűsége.
Ha egymást kizáró események vannak, akkor P(A∩B) nem történhet meg (az események nem történhetnek meg együtt), így a képlet a következő lesz:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)
Disjunkt események
A és B események disjunktek, ha:
P(A∩B) = 0
Ez csak egy másik módja annak, hogy az események kölcsönösen kizárják egymást. Nem történhetnek egyszerre.
A kapcsolódó képlet a P((A∪B)c) vagy egyenértékűen ((A∪B)’). Magyarul ez azt jelenti, hogy “nem az unió”. Ennek megoldásához számold ki az egyesülést, és az eredményt vedd el 1-től (mert az események bekövetkezésének vagy meg nem bekövetkezésének valószínűségének össze kell adódnia 1-re).
Feltételes valószínűség
P(A|B) = P(A∩B) / P(B)
A “|” jel azt jelenti, hogy “feltéve, hogy”. Más szóval annak a valószínűsége, hogy a B esemény bekövetkezik, feltéve, hogy az A esemény bekövetkezik. Példákat a képlet használatára lásd: Feltételes valószínűség.
Bayes-képlet
P(A|B) = P(B|A) – P(A) / P(B)
A feltételes valószínűség kiszámításának egyik módja a Bayes-tétel, bár kissé árnyaltabb. Dióhéjban megadja egy esemény tényleges valószínűségét a tesztekre vonatkozó információk ismeretében. Például mekkora a valószínűsége annak, hogy rákos vagy, ha az orvosi teszted pozitív (válasz = sokkal kisebb, mint gondolnád). Néhány példát lásd: Bayes-tétel példái és Posterior eloszlások / Posterior valószínűségek.
Független események
A és B esemény független, ha az egyik nem befolyásolja a másik valószínűségét. Az eseményeket akkor is függetlennek mondjuk, ha a következő egyenlet igaz.
P(A∩B) = P(A) – P(B).
Ez az egyenlet a szorzási szabályból származik, amely szerint P(A∩B) = P(A) * P(B|A). Mivel tudjuk, hogy független események esetén P(B|A) = P(B), P(B|A) helyettesíthető P(B)-vel, így megkapjuk a képletet.
Néhány megjegyzés a valószínűségi szabályokról
A statisztika a véletlenről és a becslésről szól, nem az abszolútumokról és a “helyes válaszról”. Csak nézz utána bármelyik Gallup-felmérésnek – ritkán vannak 90%-nál biztosabbak abban, hogy megvan a “helyes válasz”. Vannak technikák, amelyekkel kiszámíthatod az esélyeket (például két valószínűséget összeszorozhatsz, vagy összeadhatod őket). Azonban a binomiális eloszlási táblázaton és a fenti képleteken kívül (amelyeket a való életben nem nagyon használnak) nincsenek olyan valószínűségi képletek, amelyeket könnyen alkalmazhatnál. Vissza kell térned ahhoz a régi általános iskolai alapelemhez, a logikához (emlékszel rá… ott volt, mielőtt elkezdték a logika szabványosított tesztelését).
A valószínűségi képletek három szabálya:
- Nincsenek szabályok (vagyis nagyon kevés, kivéve a fent felsoroltakat).
- Logikát használj, ne egyenleteket.
- Sok-sok különböző módon juthatsz el a válaszhoz – ezek közül egyik sem igazán használ képleteket.
Itt egy kérdés, ami ma reggel érkezett a postaládámba, és a valószínűségekkel foglalkozik:
“Ha megpróbálnál 6 baseballkártyát gyűjteni, amelyek sajtos puffancs csomagban vannak, feltételezve, hogy egyenletesen vannak elosztva, hány csomag sajtos puffancsot kellene venned, mielőtt mind a 6 kártyát megkapod?”
A feladat megoldásának első lépése, hogy rájössz, hogy a választ nem tudod megnézni egy táblázatban. A megoldáshoz úgy kell gondolkodnod, mint egy gyerek.
1. kártya:Megint 8 éves vagy, és besétálsz egy boltba, ahol van elég pénzed, hogy vegyél egy zacskó sajtos puffancsot. Reméled, hogy mind az 5 baseballkártyát összegyűjtheted, de még nincs egy sem. Mennyi az esélye, hogy veszel egy zacskót, és kapsz egy olyan kártyát, amit szeretnél?
A válasz természetesen 100%. Vedd meg az első zsákodat, és 100% esélyed van rá, hogy olyan kártya lesz benne, amit szeretnél.
Kettes számú kártya: Most egy kicsit trükkösebb lesz a dolog. Visszatérsz a boltba, hogy megszerezd a 2. kártyát. De mivel már megkaptad az #1-es kártyát, Mickey Mantle-t. Nem akarod őt újra, de 1/5 esély van rá, hogy megkapod (és ezért 4/5 esély van rá, hogy nem kapod meg). Arányproblémává válik, hogy hány zacskó sajtos puffancsot kell venned ahhoz, hogy megszerezd a 2-es kártyát. Kitalálhatod fejben, de ha matematikailag akarod modellezni, akkor fel kell állítanod az egyenletet. Ha egy zacskó sajtos puffancs 80%-os esélyt ad a kívánt kártya megszerzésére, hány zacskót kell venned ahhoz, hogy 100%-os esélyt kapj?
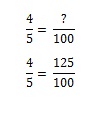
A 100% eléréséhez 1,25 zacskót kell venned.
3. kártya:Az esélyek egyre nehezebbé válnak. A harmadik baseballkártya megszerzésének esélye 60%, és a harmadik kártya megszerzéséhez 1,667 zsákot kell vásárolnod.
4. kártya:Az esélyek kezdenek kissé lehangolóvá válni. A negyedik baseballkártya megszerzésének esélye 40%, és a harmadik kártyához 2,5 zacskót kell vásárolnod.
5. kártya:Az esélyek ellened szólnak. 20% esélyed van arra, hogy megkapod az utolsó kártyát, és 5 zacskót kell venned ahhoz, hogy megszerezd a harmadik kártyát.
Az összes zacskó, amit meg kell venned, egyenlő:
1 + 1,25 + 1,667 + 2,5 + 5
De várj! (És itt jön a képbe egy kis logika). Nem mehetsz be egy boltba, és nem vehetsz 1,25 zacskó sajtos puffancsot, ezért felfelé kell kerekítened. Az egyenlet így lesz:
1 + 2 + 2 + 3 + 5 = 13 zacskó.
Egy fontos pont a képletekkel kapcsolatban: ne feledd, hogy semmi sem abszolút. Meglehetősen biztos vagyok benne, hogy ha 13 zacskó sajtos puffancsot vásárolnál, és feltételezve, hogy a kártyák egyenletesen oszlanak el, mind az 5 kártyát megkapnád. De… a valószínűség a véletlenről szól, és lehet, hogy csak a balszerencséd, hogy 10-szer egymás után ugyanazt a kártyát kapod (emlékszem, hogy gyerekkoromban ez történt velem). De lehet egy másik magyarázat is a “balszerencsédre”, mégpedig az, hogy a cégek azt akarják, hogy minél több zacskót vegyél, ezért megpróbálják az esélyeket a javukra fordítani. Még ha a kártyák egyenletesen vannak is elosztva, a cég az #1, #2 és #3 kártyákat tartalmazó zsákokat elküldheti az egyik boltba (így becsalogatva téged azzal, hogy a kártyák több mint felét összegyűjtöd), a #4 és #5 kártyákat pedig egy másik boltba.
Milyen más módot tud még elképzelni arra, hogy a gyártók a maguk javára fordítsák az esélyeket?
Az egy csoport azonos dolgot választásának valószínűsége
A valószínűségi kérdések különböző típusokra bonthatók. Amikor azt kérik, hogy találd meg annak a valószínűségét, hogy egy csoport ugyanazt a dolgot választja, akkor egy csoport (ez lehet olyan kicsi, mint egy bizottság, vagy lehet olyan nagy, mint az Egyesült Államok lakossága) véletlenszerű tagjainak cselekedeteit veszed figyelembe.
Ezek a valószínűségi kérdések egy csoportot adnak meg, és arra kérnek, hogy számítsd ki egy esemény bekövetkezésének valószínűségét a csoporton belül bizonyos számú véletlenszerű tag esetében.
Az azonos dolgot választó csoport valószínűsége : Lépések
Mintaprobléma: Egy könyvvásáron 200 ember vesz részt. Közülük 159-en legalább egy könyvet megvesznek. Ha megkérdezünk 5 véletlenszerűen kilépő embert, mekkora a valószínűsége annak, hogy mindannyian legalább egy könyvet vásároltak?

Mi a valószínűsége annak, hogy egy csoport legalább egy könyvet vásárol?
1. lépés: A kérdésben szereplő adatokat alakítsuk át törtre. Például a “159 ember 200-ból” kifejezés átalakítható a következőre: “159 ember 200-ból”: 159/200.
2. lépés: Szorozza meg a törtet önmagával. Ismételje ezt meg, ahány véletlenszerű elemet (azaz embert) választ ki. Példánkban 5 embert kérdeztek meg, tehát:
159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Így találjuk meg annak a valószínűségét, hogy egy csoport ugyanazt a dolgot választja!
Tipp: Könnyebb lehet, ha a szorzás előtt a törtet decimálisra alakítjuk. Ebben az esetben 159/200 = 0,795.
Nézd meg YouTube csatornánkat további statisztikai segítségért és tippekért! A leggyakoribb problémákra, amelyekkel valószínűleg találkozni fogsz, videókat találsz. Plusz videók az Excel használatához a statisztikában > az alapvető oszlopdiagramok készítésétől az összetett adatelemzési problémák megoldásáig.
Stephanie Glen. “Bevezetés a valószínűségszámításba: Cikkek és videók megoldásokkal!” A StatisticsHowTo.com webhelyről: Elemi statisztika a többieknek! https://www.statisticshowto.com/probability-and-statistics/probability-main-index/
——————————————————————————
Segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!




