Inleiding tot kansberekening: Artikelen en video’s met oplossingen!

Dobbelen, een parkeerplaats vinden, winnen met kaarten; Dit zijn slechts enkele situaties waarin je de kans wilt bepalen dat een gebeurtenis plaatsvindt. Als je wilt weten hoe je kansberekening maakt, moet je eerst uitzoeken wat voor soort vraag je hebt. Hoe je bijvoorbeeld de kans vindt dat een gebeurtenis plaatsvindt, is iets anders dan hoe je de kans vindt dat groepsleden hetzelfde kiezen.

Sommige kansen zijn gemakkelijk te bepalen, zoals de kans dat een dobbelsteen rolt of dat iemand een kaart uit een spel kiest.

Vragen waarbij de binomiale stelling een rol speelt, zijn ook gemakkelijk te identificeren. Bij dit soort experimenten zijn de enige mogelijke uitkomsten van een gebeurtenis “succes” of “mislukking”: zoals ja/nee, kop/staart of zwart/wit.

Andere soorten vragen die u kunt tegenkomen hebben betrekking op mensen, zoals:

• Het kiezen van een persoon uit een groep of comité.
• Kans dat een groep hetzelfde kiest.

Gebeurtenissen

Wilt u weten hoe groot de kans is dat een eenvoudige gebeurtenis plaatsvindt? Bijvoorbeeld dat het regent, of dat u een parkeerplaats vindt in de stad? Zie:
Kans dat een eenvoudige gebeurtenis plaatsvindt.
Aan de andere kant, als u precies het tegenovergestelde wilt, zie:
Hoe bepaal je de kans dat een gebeurtenis NIET plaatsvindt.

Gaat uw vraag over een gebeurtenis die plaatsvindt gegeven een andere gebeurtenis? Zoals de kans op het vinden van een parkeerplaats, gegeven dat het spelletjesdag is, of het vinden van een bepaald populair stuk speelgoed op Black Friday? Zo ja, kijk dan eens op:

• Kans op een gebeurtenis, gegeven een andere gebeurtenis.
• Twee gebeurtenissen die samen voorkomen.

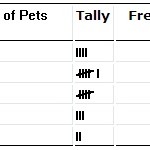
Een frequentieverdelingstabel.

Frequentieverdelingen

Heeft u een frequentieverdeling om mee te werken? Of ben je in staat om met je gegeven gegevens een frequentieverdelingstabel te maken? Bijvoorbeeld, je hebt x aantal items met een bepaalde eigenschap. Frequentieverdeling kansberekening.

Inleiding tot kansberekening: How-to artikelen en video’s.

1. Permutaties en Combinaties: How to Solve Problems
2. Probability Problems: Los ze op de gemakkelijke manier op!
3. Kans van a en b.
4. Totale kansregel.
5. Bayes Theorema Problemen: Eenvoudige oplossingsstappen.
6. Voorafgaande waarschijnlijkheid (inclusief niet-informatief en geconjugeerd).
7. Hoe maak je een waarschijnlijkheidsverdeling uit gegevens.
8. Hoe vind je de waarschijnlijkheid van het kiezen van een persoon uit een groep of comité.
9. Hoe de waarschijnlijkheid vinden van een gebeurtenis die NIET plaatsvindt.
10. Probability Frequency Distribution.
11. Hoe de waarschijnlijkheid vinden van een eenvoudige gebeurtenis die plaatsvindt.
12. Random event: Waarschijnlijkheid gegeven een percentage.
13. Hoe de waarschijnlijkheid vinden van groepsleden die hetzelfde kiezen.
14. Hoe de waarschijnlijkheid vinden van twee afhankelijke gebeurtenissen die samen optreden.
15. Hoe de waarschijnlijkheid vinden van een gebeurtenis die optreedt, gegeven een andere gebeurtenis.
16. Hoe gebruik je een waarschijnlijkheidsboom (beslisboom) om kansen te berekenen.
17. Hoe vind je de kans dat je een kaart trekt uit een kaartspel.
18. Hoe bepaal je of iets een wederzijds uitsluitende gebeurtenis is.
19. Hoe zie je het verschil tussen afhankelijke en onafhankelijke gebeurtenissen.
20. Gebruikswaarschijnlijkheid: Dobbelstenen gooien.
21. Hoe teken je een Venn-diagram.
22. Hoe maak je een Eulerdiagram.
23. 5 kies 3: hoe los je combinaties op.
24. Hoe gebruik je het fundamentele telprincipe.
25. Hoe vind je de verwachte waarde voor een discrete toevalsvariabele.

Inleiding tot kansberekening: Definities

• Axiomatische waarschijnlijkheid.
• De wet van Benford
• Wat is een binomiaal experiment?
• Basispercentages en de basispercentagefout
• Brier-scores
• Collectief uitputtend
• Wat zijn combinaties?
• Complementaire gebeurtenissen.
• Conditional Expectation
• Wat is Conditional Relative Frequency?
• Telbare additiviteit
• Lege verzameling
• Epistemische waarschijnlijkheid
• Gebeurtenisruimten.
• Wat is Experimentele waarschijnlijkheid?
• Gezamenlijke waarschijnlijkheidsverdelingen.
• Gelimiterende verdeling.
• Maximale waarschijnlijkheidsschatting
• Eigenschap zonder geheugen.
• Monte Carlo-methode.
• Monty Hall-probleem
• Wat is een wederzijds exclusieve gebeurtenis?
• Wat is een wederzijds inclusieve gebeurtenis?
• Wederzijds Onafhankelijk en Paarsgewijs Onafhankelijk.
• Wat is de Vermenigvuldigingsregel?
• Nash Equilibrium
• Niet-lege Set
• Oefeningen met normale waarschijnlijkheid.
• Wat is een normale kansberekening?
• Objectieve kansberekening
• Wat is de kansverhouding?
• Predictive Analytics
• Wat is een kansverdelingstabel?
• Kansmaat
• Wat is een kansruimte?
• Kansvectoren
• Wat zijn Steekproefruimten?
• Stochastische modellen.
• Wat is subjectieve waarschijnlijkheid?
• Wat is theoretische waarschijnlijkheid?
• Wat is een urnenmodel?

Calculators.

• On-line permutatiescalculator en combinatiescalculator.

Probabiliteitsformules / waarschijnlijkheidsregels

Een van de meest ongemakkelijke dingen die studenten niet leuk vinden aan formules is het gebrek eraan in kansberekening en statistiek. Er zijn een paar basisregels, waaronder enkele notaties die je moet kennen:

Kansbereik
0 ≤ P(A) ≤ 1
Dit stelt dat de kans op een gebeurtenis ergens tussen nul en 100% ligt (als decimaal, is dat 0 en 1). Je zult deze regel willen onthouden wanneer je waarschijnlijkheden van gebeurtenissen optelt of vermenigvuldigt. Als uw antwoord meer dan 100% is, is dat een aanwijzing dat u misschien iets verkeerd hebt gedaan.

Regel van complementaire gebeurtenissen
P(AC) + P(A) = 1
Complementaire gebeurtenissen doen zich voor wanneer er slechts twee uitkomsten zijn, zoals het opgooien van een munt. Een dobbelsteen gooien om te zien of je een zes zou krijgen is ook complementair; de enige twee uitkomsten zijn een zes krijgen (een kans van 1/6) of geen zes krijgen (kans van 5/6). De twee kansen moeten optellen tot 1.
U kunt deze formule ook als volgt geschreven zien:
p(A) + p(A’) = 1
die algebraïsch kan worden herschikt tot:
p(A’) = 1 – p(A).
Alle drie formules zijn equivalent: welke terminologie (A’ of Ac) wordt gebruikt is aan de auteur van het leerboek en aan de leraar. Persoonlijk geef ik de voorkeur aan A’, dat ik “niet A” noem. De kans op “niet A” is, denk ik, gemakkelijker te begrijpen dan “het complement” (ofwel gebeurt een gebeurtenis, ofwel gebeurt ze niet).

Toevoegingsregel
P(A∪B) = P(A) + P(B) – P(A∩B)
waar ∪ de unie is en ∩ de intersectie.
Wat dit zegt (in het Engels!) is de kans dat gebeurtenis A OF gebeurtenis B plaatsvindt (of beide tegelijk) is:

• De kans dat gebeurtenis A alleen plaatsvindt,
• Plus de kans dat gebeurtenis B alleen plaatsvindt,
• Plus de kans dat beide gebeurtenissen tegelijk plaatsvinden.

Als u gebeurtenissen hebt die elkaar uitsluiten, dan kan P(A∩B) niet gebeuren (de gebeurtenissen kunnen niet samen gebeuren), dus wordt de formule:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Gebeurtenissen die elkaar uitsluiten
Gebeurtenissen A en B zijn niet-samenhangend als:
P(A∩B) = 0
Dit is gewoon een andere manier om te zeggen dat de gebeurtenissen elkaar uitsluiten. Ze kunnen niet tegelijkertijd plaatsvinden.

Een verwante formule is P((A∪B)c) of, equivalente wijze ((A∪B)’). In het Engels betekent dit “not the union”. Om dit op te lossen, bereken je de unie en haal je de uitkomst weg van 1 (want de kans dat de gebeurtenissen wel of niet gebeuren moet optellen tot 1).

Conditional Probability
P(A|B) = P(A∩B) / P(B)
Het “|” symbool betekent “gegeven dat”. Met andere woorden, de kans dat gebeurtenis B plaatsvindt, gegeven dat gebeurtenis A plaatsvindt. Voor voorbeelden van het gebruik van de formule, zie: voorwaardelijke kans.

Bayes Formule
P(A|B) = P(B|A) – P(A) / P(B)
De stelling van Bayes is een manier om de voorwaardelijke kans uit te rekenen, hoewel die iets genuanceerder is. In een notendop, het geeft u de werkelijke waarschijnlijkheid van een gebeurtenis gegeven informatie over tests. Bijvoorbeeld, wat is de kans dat je kanker hebt als je medische test positief is (antwoord = veel lager dan je denkt). Voor enkele voorbeelden, zie: Theorema van Bayes Voorbeelden en Posterior Distributies / Posterior Waarschijnlijkheden.

Onafhankelijke gebeurtenissen
Gebeurtenissen A en B zijn onafhankelijk als de ene gebeurtenis de waarschijnlijkheid van de andere niet beïnvloedt. Men zegt ook dat gebeurtenissen onafhankelijk zijn als de volgende vergelijking opgaat.
P(A∩B) = P(A) – P(B).
Deze vergelijking is afgeleid van de vermenigvuldigingsregel, die zegt dat P(A∩B) = P(A) * P(B|A). Aangezien we weten dat P(B|A) = P(B) voor onafhankelijke gebeurtenissen, kunnen we P(B|A) vervangen door P(B), waardoor we de formule krijgen.

Enige opmerkingen over waarschijnlijkheidsregels

Statistiek gaat over toeval en ballparking, niet over absoluten en het “juiste antwoord”. Kijk maar eens naar een Gallup-peiling – ze zijn zelden zekerder dan 90% dat ze het “juiste antwoord” hebben. Er zijn technieken die je kunt gebruiken om kansen te berekenen (zoals twee kansen met elkaar vermenigvuldigen, of ze bij elkaar optellen). Maar behalve misschien de binomiale verdeeltabel en de bovenstaande formules (die in het echte leven niet zo veel gebruikt worden), zijn er niet echt waarschijnlijkheidsformules die je gemakkelijk kunt toepassen. Je moet teruggrijpen op dat oude basisonderwerp van de lagere school, de logica (je kent het nog wel… het was er vlak voordat ze begonnen met het standaard testen van de logica uit je).

De drie regels van kansformules:

1. Er zijn geen regels (nou ja, heel weinig, behalve de hierboven genoemde).
2. Gebruik logica, geen vergelijkingen.
3. Er zijn vele, vele verschillende manieren om tot het antwoord te komen – waarvan er niet echt formules worden gebruikt.

Hier is een vraag die vanmorgen in mijn inbox binnenkwam en die over waarschijnlijkheden gaat:

“Als je probeert 6 honkbalkaartjes te verzamelen die in pakjes kaasflips zitten, ervan uitgaande dat ze gelijk verdeeld zijn, hoeveel pakjes kaasflips zou je dan verwachten te kopen voordat je alle 6 de kaartjes hebt?”

Stap 1 om dit probleem op te lossen is je realiseren dat je het antwoord niet in een tabel kunt opzoeken. Om het op te lossen, moet je denken als een kind.

Kaart# 1:Je bent weer 8 jaar oud en loopt een winkel binnen met genoeg geld om één zakje kaasflips te kopen. Je hoopt alle 5 de honkbalkaartjes te verzamelen, maar je hebt er nog geen. Hoe groot is de kans dat je een zakje koopt en een kaart krijgt die je wilt?

Het antwoord is natuurlijk 100%. Koop je eerste tas, dan heb je 100% kans dat er een kaart in zit die je wilt hebben.

Card# 2: Nu wordt het een beetje lastiger. Je gaat terug naar de winkel om kaart nr. 2 te halen. Maar omdat u kaart nr. 1 al hebt, Mickey Mantle. Je wilt hem niet nog eens, maar er is 1/5 kans dat je hem krijgt (en dus 4/5 kans dat je hem niet krijgt). Hoeveel zakjes kaasflips je moet kopen om kaart nr. 2 te krijgen wordt een verhoudingsprobleem. Je zou het in je hoofd kunnen uitdokteren, maar als je het wiskundig wil modelleren moet je de vergelijking opstellen. Als je met één zakje kaasflips 80% kans hebt op de kaart die je wilt, hoeveel zakjes moet je dan kopen om 100% kans te maken?

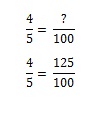
Om 100% te krijgen moet je 1,25 zakjes kopen.

Kaart # 3: De kansen worden steeds moeilijker. Je hebt 60% kans om de derde baseball kaart te krijgen, en je moet 1.667 zakken kopen om die derde kaart te krijgen.

Card# 4:De kansen beginnen een beetje somber te worden. Je hebt 40% kans op de vierde baseball kaart, en je moet 2.5 zakjes kopen om die derde kaart te krijgen.

Card# 5:De kansen zijn tegen je. Je hebt 20% kans om de laatste kaart te krijgen, en je zult 5 zakjes moeten kopen om die derde kaart te krijgen.

Dus het totale aantal zakjes dat je zult moeten kopen is gelijk aan:
1 + 1,25 + 1,667 + 2,5 + 5
Maar wacht! (En hier komt een beetje logica om de hoek kijken). Je kunt niet in een winkel 1,25 zakjes kaasflips kopen, dus moet je naar boven afronden. De vergelijking wordt:
1 + 2 + 2 + 3 + 5 = 13 zakken.

Een belangrijk punt voor formules: onthoud dat niets absoluut is. Ik ben er redelijk zeker van dat als je 13 zakjes kaasflips koopt en ervan uitgaande dat de kaartjes gelijk verdeeld zijn, dat je dan alle 5 de kaartjes zou krijgen. Maar… waarschijnlijkheid gaat over toeval, en het zou gewoon je pech kunnen zijn om 10 keer achter elkaar dezelfde kaart te krijgen (ik herinner me dat dat met mij gebeurde als kind). Maar er kan ook een andere verklaring zijn voor je “pech”, en dat is dat bedrijven willen dat je zoveel mogelijk zakjes koopt, dus zullen ze proberen de kansen in hun voordeel te laten werken. Zelfs als de kaarten gelijk verdeeld zijn, kan het bedrijf zakjes met kaarten #1, #2, en #3 naar de ene winkel sturen (en u zo binnenhalen door u meer dan de helft van de kaarten te laten verzamelen) en #4 en #5 naar een andere winkel.

Welke andere manieren kun je bedenken waarop fabrikanten de kansen in hun voordeel kunnen laten werken?

Kans dat een groep hetzelfde kiest

Waarschijnlijkheidsvragen kunnen worden onderverdeeld in verschillende typen. Wanneer u wordt gevraagd de waarschijnlijkheid te vinden dat een groep hetzelfde kiest, overweegt u de acties van willekeurige leden van een groep (die zo klein kan zijn als een comité of zo groot als de bevolking van de V.S.).
Deze kansvragen geven je een groep, en vragen je om de kans te berekenen dat een gebeurtenis zich voordoet voor een bepaald aantal willekeurige leden binnen die groep.

Kans dat een groep hetzelfde kiest : Stappen

Voorbeeldprobleem: Er zijn 200 mensen op een boekenbeurs. 159 van hen zullen ten minste één boek kopen. Als je 5 willekeurige mensen ondervraagt die uit de deur komen, hoe groot is dan de kans dat ze allemaal minstens één boek hebben gekocht?

Hoe groot is de kans dat een groep minstens één boek koopt?

Stap 1: Zet de gegevens in de vraag om in een breuk. Bijvoorbeeld, de zin “159 mensen op 200” kan worden omgezet in: 159/200.

Stap 2: Vermenigvuldig de breuk met zichzelf. Herhaal dit voor het aantal willekeurige items (d.w.z. mensen) dat is gekozen. In ons voorbeeld worden 5 mensen ondervraagd, dus willen we:

159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Zo vindt u de kans dat een groep hetzelfde kiest!

Tip: Het kan makkelijker zijn om de breuk om te zetten in een decimaal getal voordat je vermenigvuldigt. In dit geval is 159/200 = 0,795.

Bekijk ons YouTube-kanaal voor meer statistiekenhulp en -tips! We hebben video’s voor de meest voorkomende problemen die je waarschijnlijk zult tegenkomen. Plus video’s voor het gebruik van Excel in stats > alles van het maken van basis staafdiagrammen tot het oplossen van complexe data-analyse problemen.

——————————————————————————

Heb je hulp nodig bij een huiswerk- of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!