Area superficiale di un cilindro – Spiegazione ed esempi
Prima di addentrarci nell’argomento dell’area superficiale di un cilindro, esaminiamo un cilindro. In geometria, un cilindro è una figura tridimensionale con due basi circolari parallele tra loro e una superficie curva.
Come trovare la superficie di un cilindro?
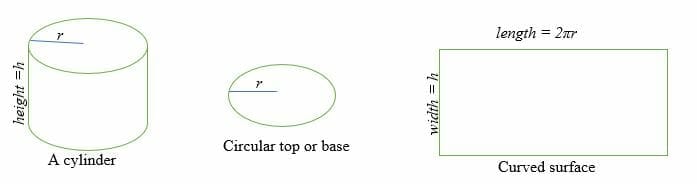
La superficie di un cilindro è la somma delle due facce circolari parallele e congruenti e la superficie curva.
Questo articolo discuterà come trovare la superficie totale e la superficie laterale di un cilindro.
Per calcolare la superficie di un cilindro, è necessario trovare l’area di base (B) e la superficie curva (CSA). Quindi, l’area della superficie o la superficie totale di un cilindro è uguale alla somma dell’area di base per due volte e l’area della superficie curva.
La superficie curva di un cilindro è uguale a un rettangolo la cui lunghezza è 2πr e la cui larghezza è h.
dove r = raggio della faccia circolare e h = altezza del cilindro.
L’area della superficie curva = Area di un rettangolo =l x w = πdh
L’area di base, B = Area di un cerchio = πr2
La formula dell’area di un cilindro
La formula della superficie totale di un cilindro è data come:
Superficie totale di un cilindro = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
dove 2πr2 è l’area della faccia circolare superiore e inferiore, e 2πrh è l’area della superficie curva.
Prendendo 2πr come fattore comune da RHS, otteniamo;
TSA = 2πr (h + r) ……………………………………. (Formula dell’area superficiale di un cilindro)
Risolviamo problemi di esempio che coinvolgono l’area superficiale di un cilindro.
Esempio 1
Trova la superficie totale di un cilindro il cui raggio è 5 cm e l’altezza è 7 cm.
Soluzione
Con la formula,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Esempio 2
Trova il raggio di un cilindro la cui superficie totale è 2136,56 piedi quadrati, e l’altezza è 3 piedi.
Soluzione
Dati:
TSA = 2136.56 piedi quadrati
Altezza, h = 3 piedi
Ma, TSA = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
Per proprietà distributiva della moltiplicazione a destra, abbiamo,
2136,56 = 18,84r + 6,28r2
Dividere ogni termine per 6,28
340.22 = 3r + r2
r2 + 3r – 340.22 = 0 ……… (un’equazione quadratica)
Solvendo l’equazione con la formula quadratica, otteniamo,
r = 17
Quindi, il raggio del cilindro è 17 piedi.
Esempio 3
Il costo della verniciatura di un contenitore cilindrico è di 0,04 $ per cm2. Trova il costo di verniciare 20 contenitori di raggio, 50 cm, e altezza, 80 cm.
Soluzione
Calcolare la superficie totale di 20 contenitori.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
La superficie totale di 20 contenitori = 40.820 cm2 x 20
=816.400 cm2
Il costo della pittura = 816.400 cm2 x $0.04 per cm2
= $32.656.
Quindi, il costo della pittura di 20 contenitori è di $32.656.
Esempio 4
Trova l’altezza di un cilindro se la sua superficie totale è 2552 in2 e il raggio è 14 in.
Soluzione
Dati:
TSA = 2552 in2
Raggio, r = 14 in.
Ma, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Dividere entrambi i lati per 87,92 per ottenere,
29.026 = 14 + h
Sottrai per 14 su entrambi i lati.
h = 15
Quindi, l’altezza del cilindro è 15 in.
Superficie laterale di un cilindro
Come detto prima, l’area della superficie curva di un cilindro è quella che viene chiamata superficie laterale. In parole semplici, la superficie laterale di un cilindro è la superficie di un cilindro, escludendo l’area della base e del fondo (superficie circolare).
La formula dà la superficie laterale di un cilindro;
LSA = 2πrh
Esempio 5
Trova la superficie laterale di un cilindro di diametro 56 cm e altezza 20 cm.
Soluzione
Dati:
Diametro = 56 cm, quindi raggio, r =56/2 = 28 cm
Altezza, h = 20 cm
Con la formula,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Quindi, la superficie laterale del cilindro è 3516,8 cm2.
Esempio 6
La superficie laterale di un cilindro è 144 ft2. Se il raggio del cilindro è di 7 piedi, trovare l’altezza del cilindro.
Soluzione
Dati;
LSA = 144 ft2
Raggio, r = 7 piedi




