Interpretare i coefficienti della regressione lineare

Impara come interpretare correttamente i risultati della regressione lineare – inclusi i casi con trasformazioni di variabili
Oggi c’è una pletora di algoritmi di apprendimento automatico che possiamo provare per trovare il migliore per il nostro particolare problema. Alcuni algoritmi hanno un’interpretazione chiara, altri funzionano come una scatola nera e possiamo usare approcci come LIME o SHAP per ricavare alcune interpretazioni.
In questo articolo, vorrei concentrarmi sull’interpretazione dei coefficienti del modello di regressione più basilare, cioè la regressione lineare, comprese le situazioni in cui le variabili dipendenti/indipendenti sono state trasformate (in questo caso sto parlando della trasformazione log).
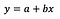
Presumo che il lettore abbia familiarità con la regressione lineare (se no c’è un sacco di buoni articoli e post su Medium), quindi mi concentrerò esclusivamente sull’interpretazione dei coefficienti.
La formula di base della regressione lineare può essere vista sopra (ho omesso i residui di proposito, per mantenere le cose semplici e al punto). Nella formula, y denota la variabile dipendente e x è la variabile indipendente. Per semplicità assumiamo che si tratti di regressione univariata, ma i principi ovviamente valgono anche per il caso multivariato.
Per metterlo in prospettiva, diciamo che dopo aver adattato il modello riceviamo:
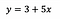
Intercetta (a)
Scomporrò l’interpretazione dell’intercetta in due casi:
- x è continua e centrata (sottraendo la media di x ad ogni osservazione, la media di x trasformata diventa 0) – la media y è 3 quando x è uguale alla media del campione
- x è continua, ma non centrato – la media y è 3 quando x = 0
- x è categorico – la media y è 3 quando x = 0 (questa volta indica una categoria, più avanti)
Coefficiente (b)
- x è una variabile continua
Interpretazione: un aumento di unità in x provoca un aumento della media y di 5 unità, tutte le altre variabili mantenute costanti.
- x è una variabile categorica
Questo richiede qualche spiegazione in più. Diciamo che x descrive il genere e può assumere valori (‘maschio’, ‘femmina’). Ora convertiamola in una variabile dummy che assume valori 0 per i maschi e 1 per le femmine.
Interpretazione: la media y è più alta di 5 unità per le femmine che per i maschi, tutte le altre variabili sono costanti.
Modello log-level
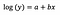
In genere si usa la trasformazione logaritmica per avvicinare i dati fuori scala di una distribuzione positivamente asimmetrica al grosso dei dati, in modo da rendere la variabile normalmente distribuita. Nel caso della regressione lineare, un ulteriore vantaggio dell’uso della trasformazione log è l’interpretabilità.
Come prima, diciamo che la formula sottostante presenta i coefficienti del modello montato.
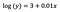
Intercetta (a)
L’interpretazione è simile a quella del caso vanilla (level-level), tuttavia, dobbiamo prendere l’esponente dell’intercetta per l’interpretazione exp(3) = 20,09. La differenza è che questo valore rappresenta la media geometrica di y (al contrario della media aritmetica nel caso del modello a livelli).
Coefficiente (b)
I principi sono di nuovo simili al modello a livelli quando si tratta di interpretare le variabili categoriche/numeriche. Analogamente all’intercetta, dobbiamo prendere l’esponente del coefficiente: exp(b) = exp(0,01) = 1,01. Questo significa che un aumento unitario di x causa un aumento dell’1% nella media (geometrica) y, tutte le altre variabili mantenute costanti.
Due cose che vale la pena menzionare qui:
- C’è una regola empirica quando si tratta di interpretare i coefficienti di un tale modello. Se abs(b) < 0,15 è abbastanza sicuro dire che quando b = 0,1 osserveremo un aumento del 10% in y per un cambiamento unitario in x. Per i coefficienti con un valore assoluto più grande, si raccomanda di calcolare l’esponente.
- Quando si tratta di variabili in intervallo (come una percentuale) è più conveniente per l’interpretazione moltiplicare prima la variabile per 100 e poi adattare il modello. In questo modo l’interpretazione è più intuitiva, poiché aumentiamo la variabile di 1 punto percentuale invece di 100 punti percentuali (da 0 a 1 immediatamente).
modello a curve progressive
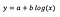
Prevediamo che dopo aver adattato il modello riceviamo:

L’interpretazione dell’intercetta è la stessa del modello a livelli.
Per il coefficiente b – un aumento dell’1% di x si traduce in un aumento approssimativo della media y di b/100 (0,05 in questo caso), tutte le altre variabili mantenute costanti. Per ottenere l’importo esatto, avremmo bisogno di prendere b× log(1,01), che in questo caso dà 0,0498.
modello log-log
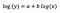
Immaginiamo che dopo il montaggio del modello riceviamo:
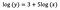
Ancora una volta mi concentro sull’interpretazione di b. Un aumento di x dell’1% si traduce in un aumento del 5% della media (geometrica) y, tutte le altre variabili mantenute costanti. Per ottenere la quantità esatta, dobbiamo prendere
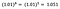
che è ~5,1%.
Conclusioni
Spero che questo articolo vi abbia dato una panoramica su come interpretare i coefficienti della regressione lineare, compresi i casi in cui alcune delle variabili sono state log-trasformate. Come sempre, qualsiasi feedback costruttivo è benvenuto. Potete contattarmi su Twitter o nei commenti.




