Introduzione alla probabilità: Articoli e video con soluzioni!

admin 0 Comments Articles

Introduzione alla probabilità: Articoli e video con soluzioni!

Lancio dei dadi, trovare un parcheggio, vincere a carte; Queste sono solo alcune situazioni in cui potresti voler trovare le probabilità che un evento accada. Se vuoi sapere come trovare la probabilità, devi prima capire che tipo di domanda hai. Per esempio, come trovare le probabilità che un evento accada è diverso dal trovare le probabilità che i membri di un gruppo scelgano la stessa cosa.

Alcune probabilità sono facili da identificare, come trovare le probabilità di lanciare i dadi o di scegliere da un mazzo di carte.

Anche le domande che coinvolgono il teorema binomiale sono facili da identificare. In questi tipi di esperimenti, gli unici risultati possibili di un evento sono “Successo” o “Fallimento”: come sì/no, testa/coda o bianco/nero.

Altri tipi di domande che potresti incontrare coinvolgono le persone, come:

• Selezione di una persona da un gruppo o comitato.
• Probabilità che un gruppo scelga la stessa cosa.

Eventi

Vuoi trovare la probabilità che un semplice evento accada? Come piovere, o trovare un parcheggio in centro? Vedi:
Probabilità che un semplice evento accada.
D’altra parte, se vuoi l’esatto contrario, vedi:
Come trovare la probabilità che un evento NON accada.

La tua domanda riguarda un evento che accade dato un altro evento? Come le probabilità di trovare un parcheggio, dato che è il giorno della partita, o di trovare un certo giocattolo popolare il venerdì nero? Se è così, controlla:

• Probabilità di un evento, dato un altro evento.
• Due eventi che accadono insieme.

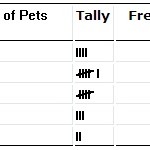
Una tabella di distribuzione di frequenza.

Distribuzioni di frequenza

Hai una distribuzione di frequenza con cui lavorare? O sei in grado di fare una tabella di distribuzione di frequenza con i tuoi dati? Per esempio, avete un numero x di articoli con un certo tratto. Distribuzione di frequenza della probabilità.

Introduzione alla probabilità: come fare per articoli e video.

1. Permutazioni e combinazioni: Come risolvere i problemi
2. Problemi di probabilità: Risolverli in modo semplice!
3. Probabilità di a e b.
4. Regola della probabilità totale.
5. Problemi del teorema di Bayes: Semplici passi per la soluzione.
6. Probabilità prioritaria (incluso disinformativo e coniugato).
7. Come fare una distribuzione di probabilità dai dati.
8. Come trovare la probabilità di selezionare una persona da un gruppo o comitato.
9. Come trovare la probabilità che un evento NON si verifichi.
10. Distribuzione delle frequenze di probabilità.
11. Come trovare la probabilità che un semplice evento si verifichi.
12. Evento casuale: Probabilità data una percentuale.
13. Come trovare la probabilità che i membri di un gruppo scelgano la stessa cosa.
14. Come trovare la probabilità che due eventi dipendenti si verifichino insieme.
15. Come trovare la probabilità che un evento si verifichi, dato un altro evento.
16. Come usare un albero delle probabilità (albero delle decisioni) per calcolare le probabilità.
17. Come trovare la probabilità di pescare una carta da un mazzo.
18. Come capire se qualcosa è un evento mutualmente esclusivo.
19. Come distinguere la differenza tra eventi dipendenti e indipendenti.
20. Probabilità: Lancio dei dadi.
21. Come disegnare un diagramma di Venn.
22. Come creare un diagramma di Eulero.
23. 5 scegliere 3: come risolvere le combinazioni.
24. Come usare il principio fondamentale di conteggio.
25. Come trovare il valore atteso per una variabile casuale discreta.

Introduzione alla probabilità: Definizioni

• Probabilità assiomatica.
• Legge di Benford
• Cos’è un esperimento binomiale?
• Tassi di base e l’errore del tasso di base
• Punteggi di Brier
• Collettivamente esaustivo
• Cosa sono le combinazioni?
• Eventi complementari.
• Aspettativa condizionata
• Che cos’è la frequenza relativa condizionata?
• Additività Contabile
• Insieme Vuoto
• Probabilità Epistemica
• Spazi degli Eventi.
• Cos’è la Probabilità Sperimentale?
• Distribuzioni di probabilità congiunte.
• Distribuzione Limite.
• Stima della massima verosimiglianza
• Proprietà senza memoria.
• Metodo Monte Carlo.
• Problema di Monty Hall
• Cos’è un evento mutuamente esclusivo?
• Mutuamente indipendenti e indipendenti a coppie.
• Qual è la regola della moltiplicazione?
• Equilibrio di Nash
• Insieme non vuoto
• Problemi pratici di probabilità normale.
• Cos’è un grafico di probabilità normale?
• Probabilità oggettiva
• Cos’è il rapporto di probabilità?
• Analisi predittiva
• Cos’è una tabella di distribuzione della probabilità?
• Misura di probabilità
• Cos’è uno spazio di probabilità?
• Vettori di probabilità
• Cosa sono gli spazi campione?
• Modelli stocastici.
• Cos’è la probabilità soggettiva?
• Che cos’è la probabilità teorica?
• Che cos’è un modello a urna?

Calcolatori.

• Calcolatrice di permutazioni e combinazioni online.

Formule di probabilità / Regole di probabilità

Una delle cose più scomode che gli studenti non amano delle formule è la loro mancanza in probabilità e statistica. Ci sono alcuni punti fermi, tra cui alcune notazioni indispensabili:

Campo di probabilità
0 ≤ P(A) ≤ 1
Questo afferma che la probabilità di un evento è da qualche parte tra zero e 100% (come decimale, è 0 e 1). Dovrai ricordare questa regola quando aggiungi o moltiplichi le probabilità degli eventi. Se la tua risposta è superiore al 100%, questo è un indizio che potresti aver fatto qualcosa di sbagliato.

Regola degli eventi complementari
P(AC) + P(A) = 1
Gli eventi complementari accadono quando ci sono solo due risultati, come lanciare una moneta. Anche lanciare un dado per vedere se si ottiene sei è complementare; gli unici due risultati sono ottenere un sei (1/6 di probabilità) o non ottenere un sei (5/6 di probabilità). Le due probabilità devono sommarsi a 1.
Si può anche vedere questa formula scritta così:
p(A) + p(A’) = 1
che può essere riorganizzata algebricamente per leggere:
p(A’) = 1 – p(A).
Tutte e tre le formule sono equivalenti: quale terminologia (A’ o Ac) sia usata dipende dall’autore del libro di testo e dall’insegnante. Personalmente, preferisco A’, che chiamo “non A”. La probabilità di “non A”, penso, è più facile da comprendere che “il complemento” (o un evento accade, o non accade).

Regola dell’aggiunta
P(A∪B) = P(A) + P(B) – P(A∩B)
dove ∪ è l’unione e ∩ è l’intersezione.
Quello che sta dicendo (in inglese!) è che la probabilità che l’evento A OPPURE l’evento B accada (o entrambi allo stesso tempo) è:

• La probabilità che l’evento A accada da solo,
• più la probabilità che l’evento B accada da solo,
• più la probabilità che entrambi gli eventi accadano allo stesso tempo.

Se si hanno eventi che si escludono a vicenda, allora P(A∩B) non può accadere (gli eventi non possono accadere insieme), quindi la formula diventa:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Eventi disgiunti
Gli eventi A e B sono disgiunti se:
P(A∩B) = 0
Questo è solo un altro modo per dire che gli eventi si escludono a vicenda. Non possono accadere nello stesso momento.

Una formula correlata è P((A∪B)c) o, equivalentemente ((A∪B)’). In inglese, questo dice “non l’unione”. Per risolverlo, calcola l’unione e togli il risultato da 1 (perché la probabilità che gli eventi accadano o non accadano deve sommarsi a 1).

Probabilità condizionata
P(A|B) = P(A∩B) / P(B)
Il simbolo “|” significa “dato che”. In altre parole, la probabilità che l’evento B accada, dato che l’evento A accade. Per esempi su come usare la formula, vedi: probabilità condizionata.

Formula di Bayes
P(A|B) = P(B|A) – P(A) / P(B)
Il teorema di Bayes è un modo per capire la probabilità condizionata, anche se è leggermente più sfumato. In poche parole, ti dà la probabilità effettiva di un evento date le informazioni sui test. Per esempio, qual è la probabilità che tu abbia il cancro se il tuo test medico è positivo (risposta = molto più bassa di quanto pensi). Per alcuni esempi, vedere: Esempi del Teorema di Bayes e Distribuzioni Posteriori / Probabilità Posteriori.

Eventi indipendenti
Gli eventi A e B sono indipendenti se uno di essi non influenza la probabilità dell’altro. Gli eventi sono anche detti indipendenti se la seguente equazione è vera.
P(A∩B) = P(A) – P(B).
Questa equazione deriva dalla regola della moltiplicazione, che dice che P(A∩B) = P(A) * P(B|A). Poiché sappiamo che P(B|A) = P(B) per eventi indipendenti, possiamo sostituire P(B|A) con P(B), dandoci la formula.

Alcune note sulle regole della probabilità

La statistica riguarda il caso e il ballparking, non gli assoluti e la “risposta giusta”. Basta guardare qualsiasi sondaggio Gallup: raramente sono più del 90% sicuri di avere la “risposta giusta”. Ci sono tecniche che si possono usare per calcolare le probabilità (come moltiplicare due probabilità insieme, o sommarle). Tuttavia, a parte forse la tabella di distribuzione binomiale e le formule di cui sopra (che nella vita reale non sono usate molto), non ci sono davvero formule di probabilità che si possano applicare facilmente. Dovete ritornare a quel vecchio punto fermo della scuola elementare, la logica (ve la ricordate… era lì proprio prima che iniziassero i test standardizzati sulla logica).

Le tre regole delle formule di probabilità:

1. Non ci sono regole (beh, molto poche, tranne quelle elencate sopra).
2. Usa la logica, non le equazioni.
3. Ci sono molti, molti modi diversi per arrivare alla risposta – nessuno dei quali usa veramente le formule.

Ecco una domanda che è arrivata nella mia casella di posta questa mattina che affronta le probabilità:

“Se stai cercando di raccogliere 6 figurine di baseball che si trovano in pacchetti di patatine al formaggio, supponendo che siano distribuite uniformemente quanti pacchetti di patatine al formaggio ti aspetti di comprare prima di avere tutte e 6 le figurine?”

Il primo passo per risolvere questo problema è capire che non puoi cercare la risposta in una tabella. Per risolverlo, devi pensare come un bambino.

Carta n. 1:Hai di nuovo 8 anni ed entri in un negozio con abbastanza soldi per comprare un sacchetto di patatine al formaggio. Speri di collezionare tutte e 5 le figurine del baseball, ma non ne hai ancora nessuna. Quali sono le probabilità che tu compri un sacchetto e riceva una carta che vuoi?

La risposta, ovviamente, è 100%. Compra il tuo primo sacchetto, e hai il 100% di possibilità che ci sia una carta che vuoi.

Carta numero 2: Ora diventa un po’ più complicato. Ritorni al negozio per prendere la carta#2. Ma siccome hai già preso la carta#1, Mickey Mantle. Non lo vuoi di nuovo, ma c’è un 1/5 di possibilità che tu possa prenderlo (e quindi un 4/5 di possibilità che tu non lo faccia). Quanti sacchetti di patatine al formaggio dovrai comprare per avere la carta n. 2 diventa un problema di rapporto. Potresti capirlo nella tua testa, ma se vuoi modellarlo matematicamente devi impostare l’equazione. Se un sacchetto di patatine al formaggio ti dà l’80% di possibilità di ottenere la carta che vuoi, quanti sacchetti devi comprare per avere il 100% di possibilità?

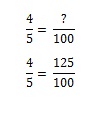
Per ottenere il 100% dovresti acquistare 1,25 sacchetti.

Card# 3: Le probabilità iniziano a diventare più difficili. Hai il 60% di possibilità di ottenere la terza carta del baseball, e dovrai comprare 1,667 sacchetti per ottenere quella terza carta.

Carta# 4:Le probabilità iniziano a diventare un po’ più basse. Hai il 40% di possibilità di ottenere la quarta carta di baseball, e dovrai comprare 2,5 sacchetti per ottenere quella terza carta.

Carta# 5:Le probabilità sono contro di te. Hai il 20% di possibilità di ottenere l’ultima carta, e dovrai comprare 5 sacchetti per ottenere quella terza carta.

Quindi la quantità totale di sacchetti che dovrai comprare è uguale a:
1 + 1,25 + 1,667 + 2,5 + 5
Ma aspetta! (E qui entra in gioco un po’ di logica). Non puoi andare in un negozio e comprare 1,25 sacchetti di patatine al formaggio, quindi devi arrotondare. L’equazione diventa:
1 + 2 + 2 + 3 + 5 = 13 sacchetti.

Un punto importante per le formule: ricordate che nulla è assoluto. Sono ragionevolmente sicuro che se avete acquistato 13 sacchetti di patatine al formaggio e supponendo che le carte siano distribuite uniformemente, otterrete tutte e 5 le carte. Ma… la probabilità riguarda il caso, e potrebbe essere solo la tua sfortuna ad ottenere la stessa carta 10 volte di fila (ricordo che mi succedeva da bambino). Ma potrebbe esserci un’altra spiegazione per la tua “sfortuna”, ed è che le compagnie vogliono che tu compri più sacchetti possibile, quindi cercheranno di far lavorare le probabilità a loro favore. Anche se le carte sono distribuite uniformemente, l’azienda potrebbe spedire i sacchetti con le carte #1, #2, e #3 ad un negozio (quindi ti attira facendoti raccogliere più della metà delle carte) e #4 e #5 ad un altro negozio.

In quali altri modi puoi pensare che i produttori possano volgere le probabilità a loro favore?

Probabilità che un gruppo scelga la stessa cosa

Le domande sulla probabilità possono essere suddivise in diversi tipi. Quando ti viene chiesto di trovare la probabilità che un gruppo scelga la stessa cosa, stai considerando le azioni di membri casuali di un gruppo (potrebbe essere piccolo come un comitato o potrebbe essere grande come la popolazione degli Stati Uniti).
Queste domande di probabilità ti danno un gruppo e ti chiedono di calcolare la probabilità che un evento si verifichi per un certo numero di membri casuali all’interno di quel gruppo.

Probabilità di un gruppo che sceglie la stessa cosa: Passi

Problema esemplificativo: Ci sono 200 persone ad una fiera del libro. 159 di loro compreranno almeno un libro. Se si intervistano 5 persone a caso che escono dalla porta, qual è la probabilità che tutti abbiano acquistato almeno un libro?

Qual è la probabilità che un gruppo acquisti almeno un libro?

Passo 1: Convertire i dati della domanda in una frazione. Per esempio, la frase “159 persone su 200” può essere convertita in: 159/200.

Passo 2: Moltiplicare la frazione per se stessa. Ripetere per quanti elementi casuali (cioè persone) vengono scelti. Nel nostro esempio, abbiamo 5 persone intervistate, quindi vogliamo:

159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Ecco come trovare la probabilità che un gruppo scelga la stessa cosa!

Suggerimento: Può essere più facile convertire la frazione in un decimale prima di moltiplicare. In questo caso, 159/200 = 0,795.

Guarda il nostro canale YouTube per altri aiuti e consigli sulle statistiche! Abbiamo video per i problemi più comuni che probabilmente incontrerai. Più video per l’uso di Excel nelle statistiche >tutto, dalla creazione di grafici a barre di base alla risoluzione di complessi problemi di analisi dei dati.

——————————————————————————

Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!