Metodo di divisione sintetica
Devo dire che la divisione sintetica è il modo più “divertente” di dividere i polinomi. Ha meno passaggi per arrivare alla risposta rispetto al metodo della divisione lunga dei polinomi. In questa lezione, andrò oltre cinque (5) esempi che si spera ti rendano familiare con le procedure di base per dividere con successo i polinomi usando la divisione sintetica.
Cose da ricordare:
- Assicurati che il dividendo sia in forma standard. Questo significa che le potenze sono in ordine decrescente.
- Il divisore deve essere nella forma x – \sinistra( c \destra).
Esempi di come dividere polinomi usando la divisione sintetica
Esempio 1: Dividere il polinomio qui sotto.
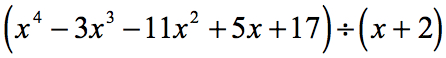
Ripercorriamo il problema dato e facciamo gli aggiustamenti necessari, se necessario.
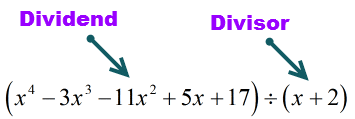
Il dividendo (roba da dividere) è in forma standard perché gli esponenti sono in ordine decrescente. Bene!
Il divisore deve essere riscritto come
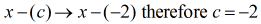
A questo punto, posso impostare la divisione sintetica estraendo i coefficienti del dividendo e poi allineandoli sopra.
Direttamente a sinistra, posizionare il valore di c = – 2 all’interno della “scatola”.
Infine, costruire una linea orizzontale appena sotto i coefficienti del dividendo.
Passi:
1. Fai cadere il primo coefficiente sotto la linea orizzontale.
2. Moltiplica quel numero che fai cadere per il numero nella “scatola”. Qualunque sia il suo prodotto, mettilo sopra la linea orizzontale proprio sotto il secondo coefficiente.
3. Aggiungi la colonna di numeri, poi metti la somma direttamente sotto la linea orizzontale.
4. Ripeti il processo finché non hai finito le colonne da aggiungere.
Vedi la soluzione animata qui sotto:
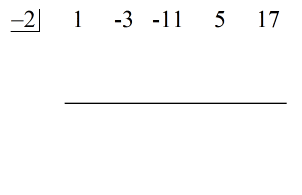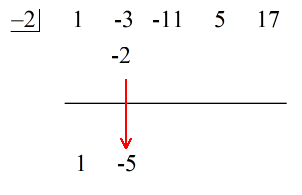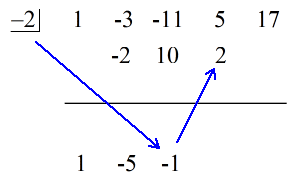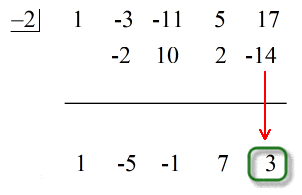
L’ultimo numero sotto la linea orizzontale è sempre il resto! Il resto di questo problema è 3.
Come presentiamo la nostra risposta finale?
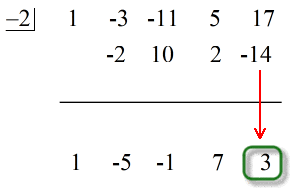
- Mostra la tua risposta finale nella forma
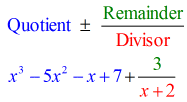
Nota che i numeri sotto la linea orizzontale tranne l’ultimo (resto) sono i coefficienti del quoziente.
Inoltre, gli esponenti delle variabili del quoziente sono tutti ridotti di 1.
Esempio 2: Dividi il polinomio.
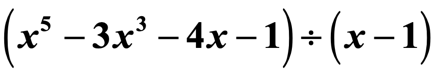
Questa non è una domanda trabocchetto. Notate che il quoziente non ha tutti gli esponenti della variabile x.
Vedo che mancano {x^4} e {x^2}. Per includere tutti i coefficienti della variabile x in potenza decrescente, dovremmo riscrivere il problema originale in questo modo. Attacca degli zeri su quelle x mancanti. Esprimere anche il divisore come x – (c) che rivela chiaramente il valore di c, cioè c = + 1.
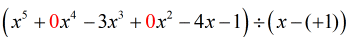
Da questo punto, posso ora impostare i numeri per continuare il processo.
Passi:
1. Fai cadere il primo coefficiente sotto la linea orizzontale.
2. Moltiplica quel numero che fai cadere per il numero nella “scatola”. Qualunque sia il suo prodotto, mettilo sopra la linea orizzontale proprio sotto il secondo coefficiente.
3. Aggiungi la colonna di numeri, poi metti la somma direttamente sotto la linea orizzontale.
4. Ripeti il processo finché non finisci le colonne da aggiungere.
Vedi la soluzione animata qui sotto:
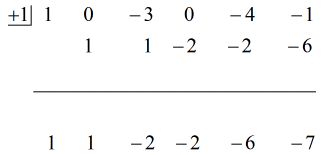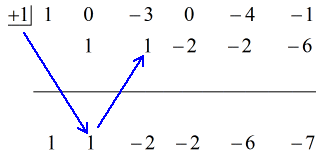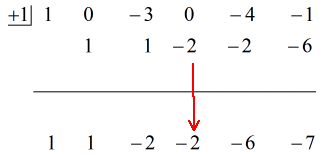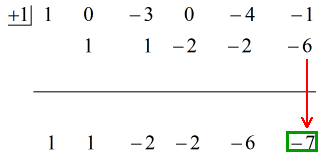
Quindi mettendo la risposta finale nella forma
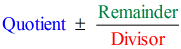
abbiamo
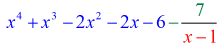
Esempio 3: Dividi il polinomio qui sotto.
Sinistra( { – 2{x^4} + x} \destra) \div \left( {x – 3} \destra)
Questo sta diventando più interessante! Il quoziente sembra decisamente orribile perché manca molto. Non solo mancano alcune x che sono {x^3} e {x^2} ma è sparita anche la costante.
Per risolvere questo, riscriverò il problema originale in modo tale che tutte le x siano considerate. Ma soprattutto, non dimenticate di includere la costante mancante che è zero.
Il problema “nuovo e migliorato” dovrebbe assomigliare a questo:
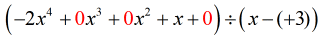
Da qui, procedete con i passi come sempre.
Passi:
1. Fai cadere il primo coefficiente sotto la linea orizzontale.
2. Moltiplica quel numero che fai cadere per il numero nella “scatola”. Qualunque sia il suo prodotto, mettilo sopra la linea orizzontale proprio sotto il secondo coefficiente.
3. Aggiungi la colonna di numeri, poi metti la somma direttamente sotto la linea orizzontale.
4. Ripeti il processo finché non finisci le colonne da aggiungere.
Vedi la soluzione animata qui sotto:
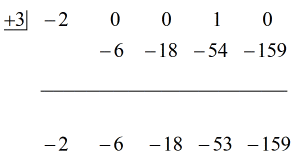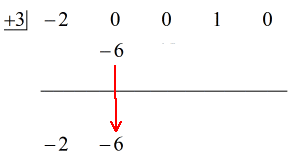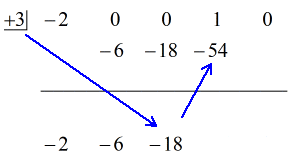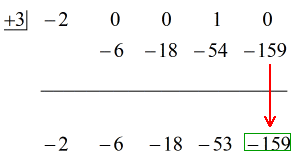
Ok allora, la risposta finale per questo è
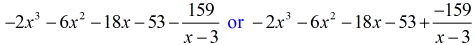
Puoi scrivere la risposta finale in due modi. Il primo è usando il simbolo del meno o della sottrazione per indicare che il resto è negativo. Il secondo è usando il simbolo + ma aggiungendo un simbolo negativo al numeratore. Significano la stessa cosa!
Esempio 4: Dividere il polinomio sottostante.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Non farti scoraggiare da questo problema. In realtà è abbastanza facile, specialmente ora che hai già fatto qualche esempio. Ricordati sempre di “riempire le parti mancanti”, giusto?
Osserva il dividendo e dovresti essere d’accordo che le parti mancanti sono {x^4}, {x^3}, {x^2} e x.
Riscrivendo il problema originale che è pronto per la divisione sintetica, otteniamo…
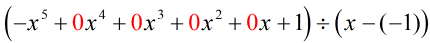
Abbiamo popolato le x mancanti con degli zeri e risolviamo esplicitamente per c = -1.
Steps:
1. Fai cadere il primo coefficiente sotto la linea orizzontale.
2. Moltiplica il numero che fai cadere per il numero nella “scatola”. Qualunque sia il suo prodotto, mettilo sopra la linea orizzontale appena sotto il secondo coefficiente.
3. Aggiungi la colonna di numeri, poi metti la somma direttamente sotto la linea orizzontale.
4. Ripeti il processo fino a quando non hai finito le colonne da aggiungere.
Vedi la soluzione animata qui sotto:
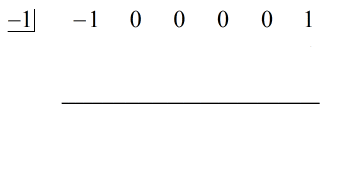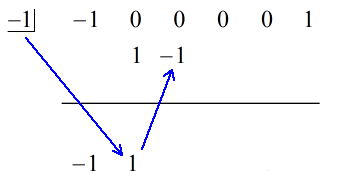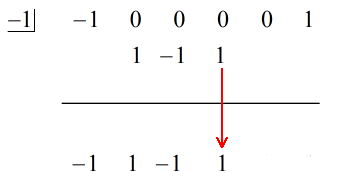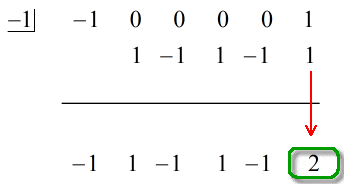
L’ultimo numero sotto la linea orizzontale sarà sempre il resto. Non dimenticarlo. In questo caso, il resto è uguale a 2.
La nostra risposta finale è
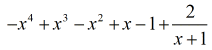
Esempio 5: Dividere il polinomio per un binomio.
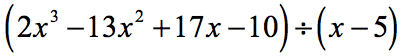
In questo esempio, avremo un resto di zero. Quando questo accade il divisore diventa un fattore del dividendo. In altre parole, il divisore divide equamente il dividendo.
Esaminando il problema, vedo che non ci sono componenti mancanti. Tutte le potenze di x sono considerate, e abbiamo una costante. Questo è fantastico! Questo problema è infatti pronto per la divisione sintetica.
Passi:
1. Fai cadere il primo coefficiente sotto la linea orizzontale.
2. Moltiplica il numero che fai cadere per il numero nella “scatola”. Qualunque sia il suo prodotto, mettilo sopra la linea orizzontale proprio sotto il secondo coefficiente.
3. Aggiungi la colonna di numeri, poi metti la somma direttamente sotto la linea orizzontale.
4. Ripeti il processo finché non finisci le colonne da aggiungere.
Vedi la soluzione animata qui sotto:
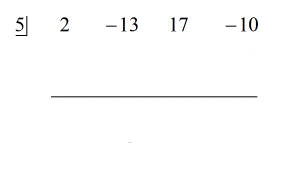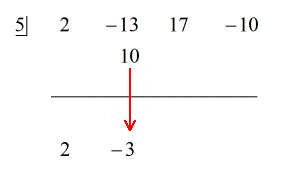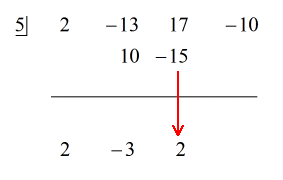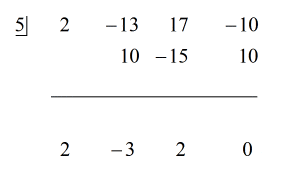
Perché il resto è uguale a zero, questo significa che il divisore x – 5 è un fattore del dividendo
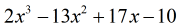
quindi
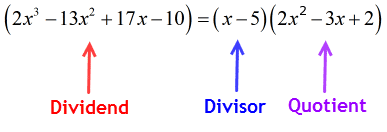
Pratica con fogli di lavoro
Ti potrebbe interessare anche:
Addizione e sottrazione di polinomi
Divisione di polinomi con il metodo della divisione lunga
Moltiplicazione di binomi con il metodo FOIL
Moltiplicazione di polinomi




