初級代数
学習目標
- 順序付きペアを描く
- 座標平面
- 座標平面上に順序対をプロットする
の構成要素を特定する。
- 座標平面上の象限を特定する
- 座標平面の4象限を特定する
- 順序対が与えられたら、次のことを行う。 2842>
座標平面は何世紀も前に(正確には1637年に)開発され、フランスの数学者ルネ・デカルトによって改良されました。 デカルトにちなんでデカルト座標系と呼ばれることもある。 座標平面は、点のプロットや直線のグラフ化に使うことができます。 このシステムは、代数的関係を視覚的に記述することを可能にし、また代数的概念の作成と解釈を助けます。
座標平面の構成要素
あなたはおそらく以前に座標平面を使ったことがあることでしょう。 たとえば、グリッドのオーバーレイを使ってオブジェクトの位置をマッピングしたことがありますか。 (これは道路地図でもよく行われます。)

この「地図」は、水平と垂直のグリッドを使って、オブジェクトの位置に関する情報を伝えているのです。 上部にA〜Fの文字が、左端に1〜6の数字が記載されていることに注目してください。 この地図では、マスに書かれた文字と数字から、大まかな位置を知ることができる。 例えば、”4F “のマスにあるものは、水平方向に指を動かし、”F “の文字から “4 “の文字に沿うようにまっすぐ下に動かすと、青いディスクがあることがわかります。 横軸と縦軸、直角に交わる数直線で構成されています。 (互いに垂直である。)
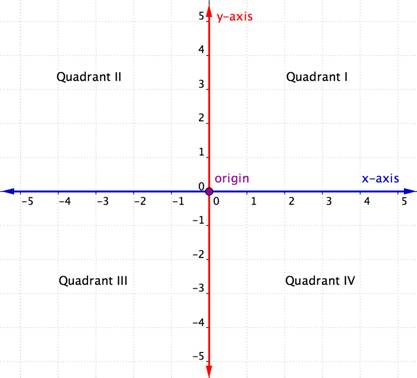
座標平面の横軸はX軸と呼ばれる。 縦軸をY軸という。 この2軸が交わる点を原点という。 原点はx軸の0、y軸の0にあります。
座標平面上の位置は順序対として記述されます。
(x, y)のような順序付きペアで、最初の値はx座標、2番目の値はy座標と呼ばれます。 x座標はy座標の前に記載されていることに注意してください。 原点はx座標が0、y座標が0なので、その順序対は(0, 0)と書かれる。
以下の点を考える。

この点の位置を特定するために、原点 (0, 0) から始めて点の下に来るまでx軸に沿って右に移動してください。 x軸のラベルを見る。 4は、原点からx軸に沿って右に4単位移動したことを示しています。 これはx座標で、順序付きペアの最初の数字である。
x軸の4から点まで移動し、y軸でそれが並んでいる数字に注目する。 3はx軸を離れてから、y軸の方向である垂直方向に3単位上へ移動したことを表している。 この数値がy座標であり、順序付きペアの2番目の数値です。 799>
例題
この点を順序付きペアとして記述します。 これがx座標で、順序付きペアの最初に書かれています。
(5, y)
5から順序付きペアに移動し、y軸の数字を読み取ります。 これがy座標で、順序対の2番目に書かれています。
(5, 2)
解答
順序対で示された点は(5, 2)です。
順序対として示された点を記述する
座標平面上の点をプロットする
X軸とY軸の使い方が分かったので、順序対もプロットできます。 どちらの処理も原点-始まり-から始まることを覚えておいてください!
Example
点 (1, 3) をプロットします。
前の例では、x座標とy座標はともに正の値でした。 順序付きペアの座標の一方(または両方)が負の場合、一方または両方の軸に沿って負の方向に移動する必要があります。
Example
点 (-4,-2) をプロットする。

x座標は順序付きペアで最初に来るので-4である。 原点からスタートし、x軸に沿ってマイナス方向(左)に4ユニット移動します。
y座標は順序の組で2番目に来るので-2です。 今度はマイナス方向(下方向)に2ユニット移動します。 y軸を見渡すと、その軸の-2と並んでいるはずです。
点をプロットする手順を以下にまとめます。
座標平面上の順序付きペア(x、y)をプロットする手順
- x座標を決定する。 原点から、x軸の方向に、x座標で与えられた距離だけ水平に移動する。 x座標が正の場合は右へ、負の場合は左へ移動します。
- y座標を決定します。 x座標を始点として、y軸の方向にy座標で与えられる距離だけ垂直に移動する。 y座標が正の場合は上に、負の場合は下に移動します。
- 終了地点に点を描きます。
座標平面上に点をプロットする
象限を特定し、点をプロットするのに使う
座標平面のx軸とy軸の交差は、それを4分割する。 この4つの区間を象限儀と呼びます。 象限は右上の象限から反時計回りにI、II、III、IVのローマ数字で名付けられます。
特定の象限内の順序付きペアは、ある特徴を持ちます。 下のグラフの各象限を見てください。 各象限内の点のx座標とy座標の符号について、何か気づきがありますか。
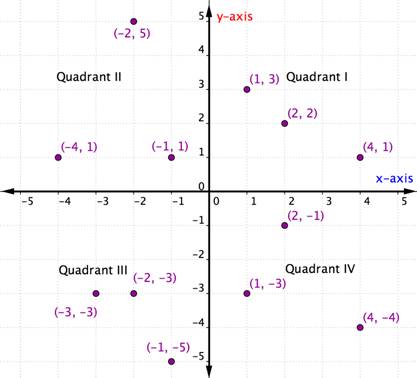
各象限内では、各順序対のx座標とy座標の符号は同じになっています。 また、下表のようなパターンがある。
| 象限 | この象限内の点の一般形 | 例 | 説明 |
|---|---|---|---|
| I | (+,+原点から、X軸を正方向(右)に、Y軸を正方向(上)に進みます。 | ||
| II | (-,+) | (-5,4) | 原点からX軸に沿ってマイナス方向(左)、Y軸に沿ってプラス方向(上)へ移動します。 |
| III | (-,-) | (-5,-4) | 原点からX軸に沿ってマイナス方向(左)、Y軸に沿ってマイナス方向(下)へ移動します。 |
| IV | (+,-) | (5,-4) | 原点からx軸を正方向(右)、y軸を負方向(下)へ進む。 |
座標平面上の象限について知っていれば、上のグラフを見れば、グラフ化しなくても順序対の象限を決定することができます。 もう一つの考え方はこちらです。
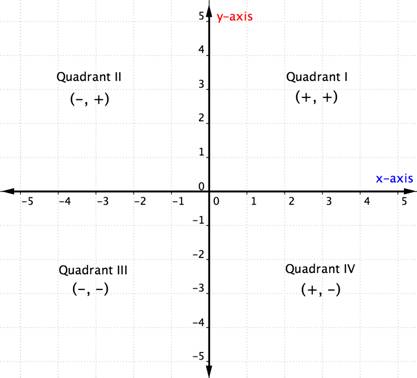
下の例では、座標の符号を考えるだけで点の象限位置を決定する方法を詳しく説明しています。 点をプロットする前に象限位置を考えておくと、ミスを防ぐことができます。
Example
点 (-7,10) はどの象限にあるか?
例題
点(-10,-5)はどの象限にあるか?
ある順序対がxまたはy座標が0の場合どうなるか? 下の例は順序付きペア(0,4)のグラフです。
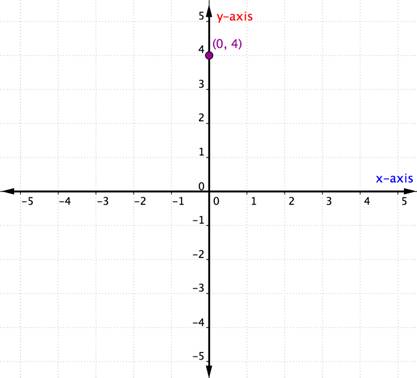
軸の1つにある点は象限にあるとは見なされません。 それは単に軸の1つ上にある。 x座標が0であるときはいつでも、点はy軸上に位置する。 同様に、y 座標が 0 の任意の点は x 軸上に位置します。
象限を識別し、それらを使用して点をプロットする
Summary
座標平面は、点と線をグラフ化し記述するためのシステムであります。 座標平面は水平(x-)軸と垂直(y-)軸で構成されている。 これらの線の交点が原点となり、それが点(0,0)となる。 座標平面は4つの象限に分割されています。 座標系のこれらの特徴を合わせると、点、線、その他の代数的な概念についてのグラフ表示やコミュニケーションが可能になる
。





