線形回帰の係数の解釈

線形回帰の結果を正しく解釈する方法を学ぶ – 変数の変換がある場合を含む
最近では、特定の問題に最も適したものを見つけるために試すことのできる機械学習アルゴリズムが数多く存在するようになりました。
この記事では、従属・独立変数が変換された場合(この場合、対数変換について話しています)を含め、最も基本的な回帰モデル、すなわち線形回帰の係数の解釈に焦点を当てたいと思います。
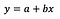
読者は線形回帰についてよく知っていると思いますので(もし知らないなら良い記事とMedium投稿がたくさんあります)、私はもっぱら係数の解釈に焦点をあてたいと思います。
線形回帰の基本式は上のようになります(シンプルかつポイントを押さえるために、あえて残差は省略しました)。 式中、yは従属変数、xは独立変数を表します。 簡単のために一変量回帰とするが、多変量の場合にも原理は当然成り立つ。
整理すると、モデルを当てはめた後、次のようになったとします。
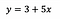
Intercept (a)
ここで、interceptの解釈を2つに分解して考えてみます。
- xが連続かつ中心である(各観測値からxの平均を引くと、変換後のxの平均は0になる)-xが標本平均
- xと同じとき平均yは3である-xが連続である。 しかし、中心を持たない – x = 0
- xはカテゴリである – x = 0のとき平均yは3(今回はカテゴリを示す、これについては後述)
係数(b)
- xは連続変数
解釈する。 xが1単位増加すると、他のすべての変数を一定とした場合、平均yが5単位増加する。
- xはカテゴリ変数
これにはもう少し説明が必要です。 xは性別を表し、値(’male’、’female’)を取れるとします。
解釈:平均yは男性よりも女性の方が5単位高く、他のすべての変数は一定とする。
ログレベルモデル
一般的に我々は正偏りの分布から外れデータをデータのバルクに引き込み、変数の正規分布化をするためにログ変換を使用します。 線形回帰の場合、対数変換を使用する追加の利点は解釈可能性です。
前回と同じく、下の式が適合したモデルの係数を示しているとします。
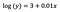
Intercept (a)
解釈はバニラ(水準値)の場合と似ていますが、解釈にはインターセプトの指数 exp(3)= 20.09 を取ることが必要です。
係数 (b)
カテゴリカル/数値変数の解釈に関しては、原理は再びレベル・レベル・モデルと同様である。 切片と同様に,我々は係数の指数を取る必要がある: exp(b) = exp(0.01) = 1.01.である. これは、xの単位増加は、他のすべての変数を一定にして、平均(幾何)yの1%増加を引き起こすことを意味します。
ここで言及すべき2つのこと:
- このようなモデルの係数の解釈に関して、経験則があります。 abs(b) < 0.15 なら、b = 0.1 のとき、x の単位変化に対して y が 10% 増加すると言ってよいでしょう。絶対値が大きい係数は、指数を計算することをお勧めします。 この方法では、100パーセントポイントではなく、1パーセントポイントずつ変数を増やしていくので、解釈がより直感的になります(0から1まですぐに)。
レベルログモデル
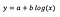
モデルのフィット後に受け取ることを想定してみましょう。

切片の解釈はレベルレベルモデルの場合と同じである。
係数bについて-xが1%増加すると、他のすべての変数が一定であれば、平均yがb/100(この場合0.05)だけおおよそ増加する。 正確な量を求めるには、b×log(1.01)を取る必要があり、この場合0.0498となる。
log-logモデル
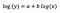
モデルのあてはめの後に得られると仮定しよう。
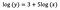
もう一度、bの解釈に着目してみます。 xが1%増加すると、他のすべての変数を一定にして、平均(幾何)yが5%増加する。 正確な量を求めるには、
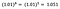
で、~5.1%となる。
結論
この記事では、変数の一部が対数変換された場合を含め、線形回帰の係数の解釈の仕方について概要を説明できたと思います。 いつものように、建設的なご意見をお待ちしています。 ツイッターやコメント欄でご連絡ください。




