Interpretacja współczynników regresji liniowej

Naucz się poprawnie interpretować wyniki regresji liniowej – w tym przypadki z transformacjami zmiennych
W dzisiejszych czasach istnieje mnogość algorytmów uczenia maszynowego, które możemy wypróbować, aby znaleźć najlepiej pasujące do naszego konkretnego problemu. Niektóre z algorytmów mają jasną interpretację, inne działają jak czarna skrzynka i możemy użyć podejść takich jak LIME czy SHAP do wyprowadzenia pewnych interpretacji.
W tym artykule chciałbym się skupić na interpretacji współczynników najbardziej podstawowego modelu regresji, czyli regresji liniowej, z uwzględnieniem sytuacji, gdy zmienne zależne/zależne zostały przekształcone (w tym przypadku mówię o przekształceniu logarytmicznym).
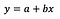
Zakładam, że czytelnik jest zaznajomiony z regresją liniową (jeśli nie, to jest wiele dobrych artykułów i postów na Medium), więc skupię się wyłącznie na interpretacji współczynników.
Podstawowy wzór na regresję liniową można zobaczyć powyżej (celowo pominąłem resztę, żeby było prosto i na temat). We wzorze y oznacza zmienną zależną, a x jest zmienną niezależną. Dla uproszczenia przyjmijmy, że jest to regresja jednoczynnikowa, ale zasady obowiązują oczywiście również dla przypadku wielowariantowego.
Aby przedstawić to w skrócie, powiedzmy, że po dopasowaniu modelu otrzymujemy:
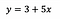
Intercept (a)
Rozłożę interpretację interceptu na dwa przypadki:
- x jest ciągły i wyśrodkowany (odejmując od każdej obserwacji średnią x, średnia przekształcona x staje się równa 0) – średnia y wynosi 3, gdy x jest równe średniej z próby
- x jest ciągły, ale nie wyśrodkowany – średnia y wynosi 3, gdy x = 0
- x jest kategoryczny – średnia y wynosi 3, gdy x = 0 (tym razem wskazując na kategorię, więcej o tym poniżej)
Współczynnik (b)
- x jest zmienną ciągłą
Interpretacja: jednostkowy wzrost x powoduje wzrost średniej y o 5 jednostek, wszystkie inne zmienne utrzymane na stałym poziomie.
- x jest zmienną kategoryczną
To wymaga nieco więcej wyjaśnień. Powiedzmy, że x opisuje płeć i może przyjmować wartości („mężczyzna”, „kobieta”). Teraz przekształćmy to w zmienną dummy, która przyjmuje wartości 0 dla mężczyzn i 1 dla kobiet.
Interpretacja: średnia y jest wyższa o 5 jednostek dla kobiet niż dla mężczyzn, wszystkie inne zmienne utrzymane na stałym poziomie.
model poziomu log
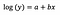
Typowo używamy transformacji logarytmicznej, aby przyciągnąć dane odstające z rozkładu dodatnio skośnego bliżej do większości danych, aby zmienna miała rozkład normalny. W przypadku regresji liniowej, jedną z dodatkowych korzyści wynikających z zastosowania transformacji log jest interpretowalność.
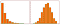
Podobnie jak poprzednio, powiedzmy, że poniższy wzór przedstawia współczynniki dopasowanego modelu.
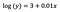
Intercept (a)
Interpretacja jest podobna jak w przypadku waniliowym (poziomowym), jednak musimy wziąć wykładnik interceptu do interpretacji exp(3) = 20,09. Różnica polega na tym, że wartość ta oznacza średnią geometryczną y (w przeciwieństwie do średniej arytmetycznej w przypadku modelu poziomicowego).
Współczynnik (b)
Przy interpretacji zmiennych kategorycznych/numerycznych zasady są znów podobne jak w przypadku modelu poziomicowego. Analogicznie do interceptu, musimy wziąć wykładnik współczynnika: exp(b) = exp(0.01) = 1.01. Oznacza to, że jednostkowy wzrost x powoduje 1% wzrost średniego (geometrycznego) y, przy wszystkich innych zmiennych utrzymanych na stałym poziomie.
Dwie rzeczy, o których warto tu wspomnieć:
- Jest pewna zasada kciuka, jeśli chodzi o interpretację współczynników takiego modelu. Jeśli abs(b) < 0.15 to można śmiało powiedzieć, że przy b = 0.1 zaobserwujemy 10% wzrost y przy jednostkowej zmianie x. W przypadku współczynników o większej wartości bezwzględnej zaleca się obliczenie wykładnika.
- Gdy mamy do czynienia ze zmiennymi przedziałowymi (jak np. procent) wygodniej jest dla interpretacji najpierw pomnożyć zmienną przez 100, a następnie dopasować model. W ten sposób interpretacja jest bardziej intuicyjna, bo zwiększamy zmienną o 1 punkt procentowy, a nie o 100 punktów procentowych (od razu z 0 do 1).
level-log model
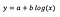
Załóżmy, że po dopasowaniu modelu otrzymujemy:

Interpretacja interceptu jest taka sama jak w przypadku modelu poziomu.
Dla współczynnika b – wzrost x o 1% powoduje przybliżony wzrost średniej y o b/100 (w tym przypadku 0,05), przy wszystkich innych zmiennych utrzymanych na stałym poziomie. Aby otrzymać dokładną wartość, musielibyśmy wziąć b× log(1.01), co w tym przypadku daje 0.0498.
model log-log
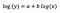
Załóżmy, że po dopasowaniu modelu otrzymujemy:
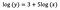
Po raz kolejny skupiam się na interpretacji b. Wzrost x o 1% skutkuje 5% wzrostem średniego (geometrycznego) y, przy zachowaniu wszystkich innych zmiennych. Aby otrzymać dokładną kwotę, musimy wziąć
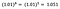
czyli ~5,1%.
Wnioski
Mam nadzieję, że ten artykuł dał Ci przegląd tego, jak interpretować współczynniki regresji liniowej, w tym przypadki, gdy niektóre ze zmiennych zostały przekształcone w log. Jak zawsze, wszelkie konstruktywne uwagi są mile widziane. Możesz się ze mną skontaktować na Twitterze lub w komentarzach.




