Bomba Centrífuga Léxico
Perdas de carga são resultado do atrito da parede em todos os tipos de tubagens e da resistência local ao fluxo, por exemplo em válvulas e acessórios (ver também Perda de carga).
Capacidades de fluxo recomendadas
- Para água fria:
Linha de sucção 0.7-1.5 m/s
Linha de descarga 1.0-2.0 m/s - Para água quente:
Linha de aspiração 0.5-1.0 m/s
Linha de descarga 1.5-3.5 m/s
A equação para a perda de carga de um caudal num comprimento recto de tubagem com secção transversal circular é:

λ Factor de atrito da tubagem
L Comprimento da tubagem em m
d Diâmetro interno da tubagem em m
v Velocidade de fluxo numa secção transversal em m/s
(= 4 Q / π d2 com Q em m3/s)
g Aceleração devido à gravidade em m/s2
ver Fig. 1 e 4 Perda de carga
>O factor de atrito da tubagem foi estabelecido experimentalmente. Ele depende apenas do estado do fluxo do fluido manuseado e da rugosidade relativa (d/k) dos tubos através dos quais o fluido está a fluir. Para secções transversais de tubos não circulares aplica-se o diâmetro equivalente em termos fluido-mecânicos (d):

A Secção transversal em m2
U Perímetro da secção transversal molhada em m
(a superfície livre de um canal aberto não é considerada)
> O estado de escoamento é determinado pelo número de Reynolds (Re) de acordo com as leis de afinidade. O seguinte aplica-se a tubos circulares:
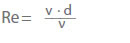
v Velocidade de fluxo numa secção transversal em m/s
(= 4 Q / π d2 com Q em m3/s)
ν Viscosidade cinemática em m2/s
(para água a 20 °C: 1.00 – 10 – 6 m2/s)
d Diâmetro interno do tubo em m
Ver Fig. 4 Perda de carga
Para tubos lisos hidraulicamente, como tubos lisos de metal ou plástico (por exemplo, PE ou PVC), ou no caso de fluxo laminar, o fator de atrito do tubo (λ) pode ser calculado. Para um fluxo laminar num tubo com um número Reynolds inferior a 2320, o factor de atrito do tubo é independente da rugosidade:
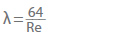
Se o fluxo for turbulento, ou o número Reynolds for superior a 2320, o factor de atrito do tubo em tubos lisos hidraulicamente pode ser representado por uma equação empírica de acordo com Eck (devido ao facto de os desvios serem inferiores a 1% se o número Reynolds for inferior a 108).

O factor de atrito da tubagem (λ) também depende de um outro parâmetro sem dimensões, ou seja, da rugosidade relativa da superfície interior da tubagem (d/k). Ambos devem ser especificados na mesma unidade (por exemplo, mm).
Ver Fig. 1 Perda de carga
>
(k) é a rugosidade média absoluta da superfície interna do tubo para a qual estão disponíveis valores aproximados, dependendo do material e dos processos de fabricação. Ver Fig. 2 Perda de cabeça
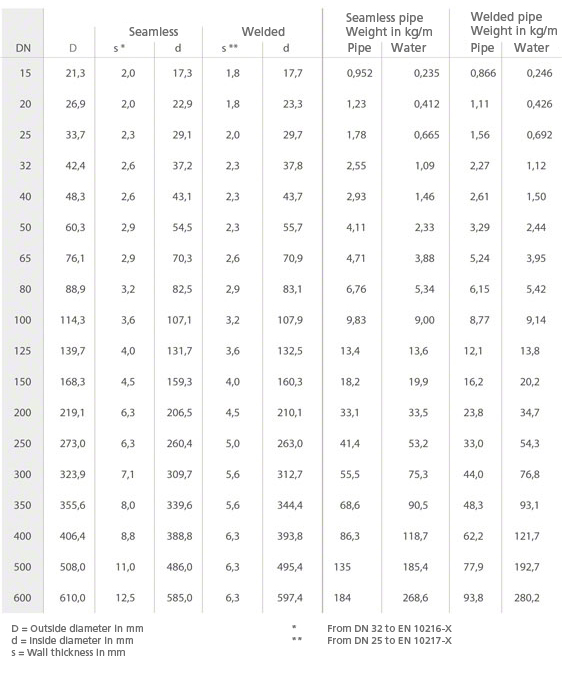 Fig. 2 Perda de cabeça: Estimativas das alturas médias pico a vale k (rugosidade absoluta) dos tubos
Fig. 2 Perda de cabeça: Estimativas das alturas médias pico a vale k (rugosidade absoluta) dos tubos
Acima da curva limite, o fator de atrito do tubo (λ) depende apenas da rugosidade relativa do tubo (d/k). Ver Fig. 1 Perda de carga
A seguinte equação empírica de Moody pode ser usada para esta região:

Para uso prático, a perda de carga (HL) por 100 m de tubo de aço reto é mostrada no diagrama em função da vazão (Q) e do diâmetro interno do tubo (d).
Ver Fig. 3 Perda de carga
Os valores são válidos apenas para água fria e limpa ou para fluidos com a mesma viscosidade cinemática, para tubos completamente cheios e para rugosidade absoluta da superfície interna do tubo de k = 0.05 mm.
Dimensões, pesos, enchimento de água para novos tubos de aço sem costura ou soldados longitudinalmente
Ver Anexo, Perda de carga, Fig. 4
O efeito de uma rugosidade superficial aumentada k será demonstrado a seguir para um conjunto de intervalos de parâmetros frequentemente utilizados (diâmetro nominal DN = 50 a 300, velocidade de fluxo v = 0,8 a 3,0 m/s). Ver Fig. 3 Perda de carga
A região azul claro corresponde à região igualmente marcada para uma rugosidade média absoluta de k = 0,05 mm.
Ver Fig. 1 Perda de carga
Para uma rugosidade aumentada por um fator de 6 (tubo de aço velho ligeiramente incrustado com k = 0,30 = 300 μm (0.30 mm), os fatores de atrito do tubo (e as perdas de carga proporcionais associadas) na região azul escuro são apenas 25 – 60% maiores do que antes.
Ver Fig. 1 Perda de carga
Para tubos de esgoto, o aumento da rugosidade causada pela sujeira deve ser levado em consideração. Para tubos sujeitos a incrustações extremas, a perda de carga real só pode ser determinada experimentalmente. Desvios do diâmetro nominal alteram consideravelmente a perda de carga, uma vez que o diâmetro interno do tubo apresenta na equação a 5ª potência.
A 5 % de redução do diâmetro interno, por exemplo, leva a um aumento da perda de carga em até 30 %. Portanto, é importante que o diâmetro interno não seja simplesmente substituído pelo diâmetro nominal nos cálculos.
As perdas de cabeça em tubos de plástico ou tubos metálicos estirados lisos são muito baixas, graças às superfícies lisas dos tubos. As perdas de cabeça estabelecidas são válidas para água a 10 °C. A outras temperaturas, as perdas de cabeça em tubos de plástico devem ser multiplicadas por um factor de correcção de temperatura especificado para ter em conta a sua maior expansão térmica. Para águas residuais ou outras águas não tratadas, deve ser considerada uma perda de carga adicional de 20-30 % para potenciais depósitos.
Perdas de carga para tubos de plástico e metal estirado liso
Ver Anexo, Perdas de carga, Fig. 5
Perdas de carga nas válvulas e acessórios
A perda de carga (HL) nas válvulas e acessórios é dada por:
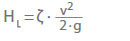
>ζ Coeficiente de perda
Ver Figs. 6 a 12 Perda de carga
v Velocidade de fluxo em uma área transversal característica A
(ex. no bico) em m/s
g Aceleração devido à gravidade 9,81 m/s2
 Fig. 6 Perda de carga: Diagrama esquemático dos desenhos das válvulas
Fig. 6 Perda de carga: Diagrama esquemático dos desenhos das válvulas
 Fig. 11 Perda de carga: Influência no coeficiente de perda ζ do arredondamento do lado interno e externo dos cotovelos em ductos quadrados
Fig. 11 Perda de carga: Influência no coeficiente de perda ζ do arredondamento do lado interno e externo dos cotovelos em ductos quadrados
>
 Fig. 12 Perda de carga: Coeficientes de perda ζ para válvulas borboleta, globo e válvula de gaveta dependendo do grau de abertura
Fig. 12 Perda de carga: Coeficientes de perda ζ para válvulas borboleta, globo e válvula de gaveta dependendo do grau de abertura
As perdas atribuíveis ao endireitamento dos distúrbios de caudal num comprimento de tubo equivalente a 12 x DN a jusante da válvula estão incluídas nos coeficientes de perda de acordo com a directriz VDI/VDE 2173. Os valores aplicam-se às válvulas que têm um caudal de aproximação estável, são totalmente abertas e operadas com água fria. Dependendo das condições de fluxo de entrada e saída, dos modelos de válvulas e dos objectivos de desenvolvimento (ou seja, válvulas de baixo custo ou de baixo consumo energético), os valores de perda podem variar drasticamente. Ver Anexo, Perda de carga, Fig. 7
Amaciacia o valor kv é usado em vez do coeficiente de perda (ζ) ao calcular a perda de carga para água nas válvulas:
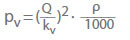
O valor kv é o caudal em m3/h que resultaria de uma perda de carga pv = 1 bar através da válvula para água fria. Ele descreve a correlação entre a perda de pressão (pL) em bar e o caudal (Q) em m3/h. Conversão para coeficiente de caudal ζ para água fria:
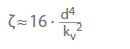
d Diâmetro de referência (nominal) da válvula em cm
Para o cálculo das perdas de carga em acessórios, acessórios de derivação e adaptadores requerem uma abordagem diferente. Ver Figs. 9 e 10 Perda de carga
 Fig. 9 Perda de carga: Coeficientes de perda ζ para acessórios
Fig. 9 Perda de carga: Coeficientes de perda ζ para acessórios  Fig. 10 Perda de carga: Coeficientes de perda ζ para adaptadores
Fig. 10 Perda de carga: Coeficientes de perda ζ para adaptadores
Para todas as conexões deve ser feita uma diferenciação entre duas formas de perda de pressão:
- Perdas de pressão irreversíveis (redução de pressão)
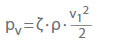
>
pv Perda de pressão em Pa
ζ Coeficiente de perda
ρ Densidade em kg/m3
v Velocidade de fluxo em uma cross-secção em m/s
- Mudanças de pressão reversíveis do fluxo sem fricção de acordo com a equação de Bernoulli
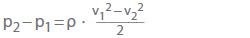
Para fluxos acelerados tais como reduções no diâmetro do tubo, (p2 – p1) é sempre negativo; para fluxos desacelerados, tais como expansões de tubos, é sempre positivo. Ao calcular a variação de pressão líquida como a soma aritmética de pL e (p2 – p1), as perdas de pressão irreversíveis devem ser sempre subtraídas.
Influência de fluidos altamente viscosos na curva característica do sistema
Como as leis da dinâmica dos fluidos mantêm sua validade para todos os fluidos newtonianos, as equações e diagramas para o cálculo dos fatores de atrito da tubulação e coeficientes de perda para válvulas também são aplicáveis a fluidos viscosos com viscosidade maior que a água.
Ao calcular o número Reynolds Re = v – d / ν , deve-se simplesmente substituir a viscosidade cinemática dos fluidos viscosos νz pela viscosidade da água νz.
Isto produz um menor número de Re e, de acordo com a Fig. 1 Perda de carga, um maior coeficiente de atrito do tubo λz (Nota: a influência da rugosidade da parede pode agora ser frequentemente ignorada por causa da maior espessura da camada limite no fluxo).
Todas as perdas de carga nos tubos e válvulas calculadas para água devem ser extrapoladas usando a razão νz/λw.
Figure 13 A perda de carga também é adequada para uso prático geral: o fator de fricção da tubulação λz pode ser determinado rapidamente em função da vazão Q, diâmetro interno da tubulação d e viscosidade cinemática νz. Deve-se ter em conta, no entanto, que o coeficiente λw neste diagrama só é válido para tubos lisos hidraulicamente (ou seja, não para tubos rugosos)! O correspondente λw pode ser utilizado para calcular a razão λz/λw.
Como o componente estático da curva característica do sistema Hsys , veja Fig. 1 Curva característica do sistema e Fig. 2 Cabeça, não é afetado pela viscosidade, o componente dinâmico da curva característica do sistema para água pode ser redesenhado como uma parábola mais íngreme para um fluido viscoso.
Influência de fluidos não-Newtonianos na curva característica do sistema
Como as curvas de fluxo não são linhas retas de viscosidade linear constante, o cálculo das perdas de carga é muito pesado. Neste caso, o cálculo das perdas é baseado na experiência com fluidos particulares.




