Equações da Mecânica Relativista e Quântica (sem Giro)
Introdução
-Duvidar de tudo ou acreditar que tudo são duas soluções igualmente convenientes;
Dispensa-se tanto da necessidade de reflexão.
Henri Poincaré (1854-1912)
Eu sei, eu sei, mas suponha – suponha! – a pureza do círculo nos cegou de ver qualquer coisa além dele!
Devo começar tudo de novo com novos olhos, devo repensar tudo!
Hypathia (∼360-415 AD)
Em 1913, Bohr, baseado nas fórmulas empíricas de Balmer, construiu um modelo de átomo baseado na quantização do momentum orbital , que foi posteriormente suplementado pelas regras mais gerais de quantização de Sommerfeld. Naqueles anos, naturalmente, a presença de um spin ou momento magnético intrínseco da partícula ou, especialmente, a interação spin-orbit, ou interação com o spin nuclear, não era suposta.
Em 1916, Sommerfeld, no quadro de abordagens relativistas, derivou uma fórmula para os níveis de energia de um átomo semelhante ao hidrogênio, sem levar em conta o spin . Sommerfeld procedeu a partir do modelo do átomo de Bohr e usou a relação relativista entre o momentum pand a energia E De uma partícula livre com a massa m.
onde cis a velocidade da luz.
Num campo externo com um potencial tetradimensional (φ,A), supunha-se que para uma partícula com a carga qesta relação também pode ser usada se subtrairmos os componentes do momento tetradimensional do campo (qφ,qA) da expressão para o momento de partícula generalizado:
No caso do potencial Coulomb φ=Ze/r, onde e é a carga de elétron, sobe a distância do núcleo, e Zis um número atômico, obtemos em coordenadas esféricas
onde Lis o momento angular. As condições de quantização de Bohr-Sommerfeld tomam a forma
where nφand nr são os números quânticos orbital e radial, respectivamente. Para os níveis de energia, Sommerfeld obteve a fórmula
onde o número quântico principal n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, e α=1/137.036 é a estrutura fina constante. Entretanto, em um trabalho publicado em 1916, Sommerfeld ‘cometeu um feliz erro’ e a fórmula derivada foi apresentada na seguinte forma
A fórmula (6) descreveu perfeitamente todas as peculiaridades da estrutura do espectro do hidrogênio e outros átomos semelhantes com a limitação para aqueles anos da precisão das medidas, e não havia dúvidas sobre a correção da própria fórmula. Portanto, a fórmula de Sommerfeld foi percebida como empírica, e em vez do número quântico l, um número quântico interno ‘misterioso’ com valores meio-inteiros j=1/2,3/2,5/2,…,n+1/2 foi introduzido, e a fórmula (6) foi utilizada na representação
where n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, e l possuem os valores l=0 em j=1/2 e l=j±1/2 para outros. Esta fórmula coincide com o resultado de uma solução exata das equações relativistas de Dirac em 1928 para uma partícula com o spin 1/2 com a expressão clássica para a energia potencial de uma carga imóvel no campo Coulomb de um núcleo com um número atômico Zin a forma Ur=Ze2/r.
Fórmula (7) também indicou uma estranha limitação de valor a carga de um núcleo com o número atômico Z<137, acima da qual a fórmula está perdendo o seu significado. Foi também evidente que, no quadro das abordagens delineadas, as interacções fortes e gravitacionais, os movimentos dos planetas não são descritos. O problema Z<137 ou α>1rema o problema não resolvido da mecânica quântica relativista. Expandindo a fórmula (7) pela ordem das potências Zα2in a série Taylor, com uma precisão de expansão até os termos pelas potências Zα6, obtemos
Em 1925-1926, Schrödinger trabalhou na derivação da equação para a função de onda de uma partícula descrevendo as ondas De Broglie . A derivação da equação também foi baseada na relação relativista (1) entre o momentum pand a energia E da partícula, que ele apresentou com a ajuda dos operadores de quadrados de energia e momentum na forma de uma equação para a função da onda
>
Like Sommerfeld, Schrödinger utilizou a seguinte representação para uma partícula num campo externo
No caso de estados estacionários de um partícula carregada no campo do potencial Coulomb para um átomo de hidrogênio foi necessário resolver a equação
As pode ser visto, a expressão quadrática da energia potencial q2φ2r/2mc2 está presente na equação com um sinal positivo e, no caso de atrair campos, as soluções levam a certas dificuldades. Ao aproximar-se do ponto de singularidade, devido ao sinal negativo, as forças de atração aumentam e a presença da singularidade leva a limitações conhecidas sobre a magnitude das interações (Figura 1).
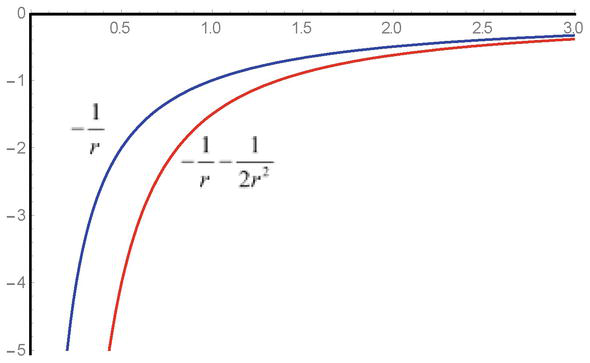
Figure 1.
A dependência da amostra do potencial de interação potencial de campo atrativo-1/r-1/2r2 nas equações de Klein-Gordon.
Próximo, o vetor de onda kis representado como
e ao considerar o problema da passagem de uma partícula com energia Eth através de uma barreira potencial U=qφr(Figura 2), cuja altura é superior ao dobro da energia de repouso da partícula U>2mc2 , o coeficiente de transmissão torna-se unidade, independentemente da altura da barreira (paradoxo de Klein) .
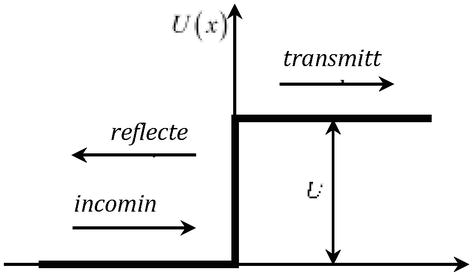
Figure 2.
Passagem de uma partícula através de uma barreira potencialU.
Outra dificuldade é que, como a solução do problema da partícula em um poço potencial mostra, a uma profundidade suficiente, uma partícula com comprimento de onda ƛ=ℏ/mccan tem estados ligados (podem ser localizados) em uma largura de poço mais estreita do que o comprimento de onda da partícula d<ƛ/2(Figura 3), o que contradiz o princípio fundamental da mecânica quântica – o princípio da incerteza de Heisenberg.
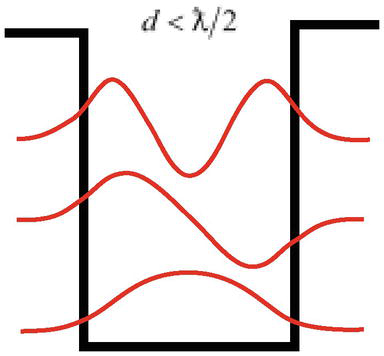
Figure 3.
Uma partícula com um wavelengthƛcan seja localizada em uma largura de poço d<ƛ/2.
Também, a solução do problema de um átomo semelhante ao hidrogênio é limitada pelo valor do número ordinal do núcleo atômico Z≤68(para a equação de Dirac, a restrição do número atômico é Z≤137). O mesmo em mecânica relativista – quando considerando as fortes interações, a solução da equação relativista de Hamilton-Jacoby indica a chamada “queda de partículas no centro” .
Para se livrar do termo quadrático ou reverter seu signo, nos últimos anos tem sido proposto representar a energia potencial nas equações de Klein-Gordon e Dirac como a diferença dos quadrados das expressões dos potenciais escalar e vetoriais (equação da onda S) . Tal formalismo matemático corrige a situação, mas do ponto de vista físico tais representações não são de forma alguma justificadas, e os campos correspondentes a tais pseudo-potenciais não existem na natureza.
As coisas são ainda piores com a presença de um termo quadrático do campo vetorial, por causa do sinal do qual obtemos estados inexistentes na natureza e soluções que contradizem a experiência.
De acordo com as soluções das equações da mecânica quântica e Hamilton-Jacoby, acontece que uma partícula carregada em um campo magnético, além de girar em um círculo, também tem vibrações radiais – níveis Landau (mesmo no caso de momento orbital zero).
No decorrer destes 90 anos, especialmente em experiências de ressonância cíclotron muito precisas, nenhuma detectou as vibrações radiais dos electrões e os níveis de Landau.
Solucionando esta equação, Schrödinger, como Sommerfeld, recebeu a fórmula (5), que descreveu a estrutura do espectro do hidrogênio não exatamente. Além disso, a partir da solução do problema para uma partícula num poço potencial, verifica-se que uma partícula com um comprimento de onda ƛ=ℏ/mchas bound states (é colocada) num poço de tamanho arbitrário e, em particular, muito menor do que ƛ/2. Este facto contradiz o princípio fundamental da teoria quântica (onda), o princípio da incerteza.
Em 1925 Schrödinger enviou este trabalho aos editores de ‘Annalen der Physik’, mas depois tomou o manuscrito, recusou as abordagens relativistas e em 1926 construiu uma equação de onda baseada na expressão clássica Hamiltoniana, a equação de Schrödinger .
Equação descreveu o espectro do átomo de hidrogênio apenas qualitativamente, no entanto, não tinha nenhuma restrição irracional ou soluções singulares na forma da fórmula de Sommerfeld-Dirac. Klein , Fock e Gordon publicaram a equação relativista baseada na equação da onda para uma partícula sem spin em 1926; é chamada de equação de Klein-Fock-Gordon.
Com a descoberta do spin, a situação mudou drasticamente, e em 1926 Heisenberg e Jordan mostraram que, dentro da descrição Pauli do spin de um elétron, metade da energia da interação spin-orbit é igual a um termo com um poder de α4 na expansão da série Taylor da referência da equação da fórmula de Sommerfeld vai aqui.
Por que exatamente a metade, Thomas tentou explicar isso em 1927 pela presença de uma precessão relativista de um elétron no quadro de referência do movimento ao longo da órbita . A energia da precessão de Thomas é exatamente igual a metade do valor da energia da interação spin-orbit com o sinal inverso (positivo), que deve ser adicionado à energia da interação spin-orbit. No entanto, a hipótese incorrecta de que a frequência da precessão de Thomas é idêntica nos dois quadros de referência e a ausência de uma derivação comum e correcta para quadros de referência não-iniciais (rotativos) levantou dúvidas sobre a correcção de tais abordagens. A razão para o aparecimento da metade da energia da interação spin-orbit na fórmula de Sommerfeld ainda está sob investigação e é um dos problemas não resolvidos na física moderna.
Por outro lado, tanto na derivação da fórmula de Sommerfeld como na solução da equação de Klein-Fock-Gordon para o problema do átomo de hidrogênio, nem a energia da interação spin-orbit foi levada em conta inicialmente. Portanto, a divisão fina obtida não pode de forma alguma ser devida à interação spin-orbit. Este é um efeito relativista mas puramente mecânico, quando a massa (inércia) de uma partícula já depende da velocidade de movimento ao longo da órbita (do momento angular), devido ao qual o movimento radial do elétron muda, e vice-versa. Apenas esta dependência, que resulta na divisão dos níveis energéticos do electrão, e à impossibilidade de introduzir apenas um, o número quântico principal. No entanto, mesmo com esta hipótese, a ordem de divisão dos níveis segundo a fórmula (8) contradiz a lógica; acontece que quanto maior o momento angular orbital, menor a energia da divisão do nível.
A representação matricial da onda Eq. de segunda ordem. (9) por um sistema de equações de primeira ordem é a construção de Dirac da equação do elétron relativista (as matrizes de Dirac são a representação particular dos números de Clifford-Lipschitz ). Na representação padrão, a equação de Dirac para uma partícula livre tem a forma .
where
são as matrizes de Pauli (a matriz unitária nas fórmulas é omitida).
Para uma partícula em um campo externo, Eq. (16) é geralmente escrito no formulário
onde para uma representação invariante no caso de uma partícula livre, as equações são compostas para a diferença entre o momento generalizado e o momento do campo.
No caso da energia potencial de uma carga imóvel em um campo Coulomb, obtemos a fórmula Sommerfeld-Dirac como resultado de uma solução exata desta equação em particular. Lá, novamente, embora para um sistema com spin 1/2 a energia da interação spin-orbit não é levada em conta inicialmente, mas a metade é obtida a partir da solução exata do problema do átomo de hidrogênio.
Medições mais precisas de Lamb em 1947 e melhorias subsequentes no espectro do átomo de hidrogênio revelaram que, além das linhas com o j máximo, todas as outras também são divididas e um pouco deslocadas (o deslocamento de Lamb). Para harmonizar os resultados da teoria com dados experimentais mais precisos sobre o espectro do átomo de hidrogênio, era preciso propor outras soluções e abordagens do que as estabelecidas pela derivação da equação de Dirac.
As novas abordagens teóricas nada tinham produzido e apenas complementaram a teoria com as propostas ilógicas e não físicas para superar a singularidade emergente das soluções: a renormalização, a diferença finita de infinitos com o valor desejado da diferença, e assim por diante. A contabilização do tamanho do núcleo corrigiu apenas o valor Z para o valor maior, mas não resolveu o problema Z>137. Um resultado incrível também foi obtido para o problema do átomo de hidrogênio que o elétron está localizado, muito provavelmente, no centro do átomo, ou seja, no núcleo.
Os resultados da solução do problema para uma partícula em um poço potencial tanto no caso da equação de Klein-Fock-Gordon quanto da equação de Dirac contradizem o princípio básico da mecânica quântica, o princípio da incerteza. Das soluções, resulta que uma partícula pode estar em estado ligado num poço com quaisquer dimensões, em particular, com o tamanho muito menor que o comprimento de onda da própria partícula, A=ℏ/mc.
Embora o próprio Dirac tenha proposto um sistema de equações relativistas lineares de primeiro grau na representação matricial que descreveu o sistema com spin 1/2, as contradições não desapareceram, e ele próprio permaneceu descontente com os resultados da sua teoria. Como Dirac escreveu em 1956, o desenvolvimento da teoria dos electrões relativistas pode agora ser considerado como um exemplo de como argumentos incorrectos por vezes conduzem a um resultado valioso. Nos anos 70, tornou-se claro que a teoria relativista da mecânica quântica não existe, e novas abordagens e equações fundamentais devem ser procuradas para a construção de uma teoria consistente da mecânica quântica relativista. E nos anos 80, Dirac já falava das dificuldades insuperáveis da teoria quântica existente e da necessidade de criar uma nova .
A razão do fracasso destas teorias é bastante simples – está no ignorar da dependência da energia de interação com o campo da velocidade da partícula. O momento generalizado do sistema, a partícula mais o campo externo, é a soma da expressão relativista para o momento mecânico da partícula e o momento de campo no caso da interacção com a partícula imóvel
que não é uma representação invariante da velocidade da partícula. Para construir alguma invariância a partir dessa representação, foi utilizada uma relação ‘invariante’ em todos os casos na forma de uma diferença entre o momento generalizado do sistema e o momento de campo no caso da interação com a partícula imóvel
Obviamente, a permutação dos componentes do impulso generalizado para a construção do invariante não resolve o problema colocado. A afirmação de que a expressão (20) é o momento mecânico de uma partícula e, portanto, é uma invariante não está comprovada e é necessário apreender a fórmula (20) como um empírico. Portanto, em altas velocidades ou fortes interações, uma dependência inexplicável da energia de interação da partícula com o campo da velocidade do movimento da partícula, que resulta nos resultados errôneos ou na impossibilidade de cálculos.
Em , foi sugerida uma representação invariável do momento generalizado do sistema, onde se levou em conta a dependência da energia de interação da partícula com o campo em relação à velocidade:
que é a representação tetradimensional do momento generalizado do sistema baseado na expressão para o momento generalizado de uma partícula imóvel em estado de repouso
cujo invariante é sempre igual à expressão (19) independentemente do estado do sistema.
A aplicação de princípios variacionais para construir a teoria relativista e quântica foi baseada nos princípios de construção da mecânica com a ajuda do Lagrangiano do sistema , que originalmente não era destinada a abordagens relativistas. A construção Lagrangiana é paramétrica com a variável unidimensional τ = ct, destacada das variáveis do espaço tetradimensional (as demais são representadas pela dependência desta variável τ) e contém o diferencial total em relação a esta variável, a velocidade da partícula. Tal construção é inaceitável devido à impossibilidade de aplicar o princípio da invariância da representação das variáveis e a representação covariante da ação do sistema.
In , para construir a teoria relativista com base em princípios variacionais, as soluções canônicas (não paramétricas) do problema variacional para as funções integrais canonicamente definidas foram consideradas e as soluções canônicas dos problemas variacionais da mecânica nos espaços Minkowski são escritas. Devido à unificação dos princípios variacionais de menor ação, fluxo e hiperfluxo, as equações canônicas invariantes para o momento generalizado são obtidas. A partir destas equações, as expressões para a função ação e para a função onda são obtidas como solução geral do problema variacional unificado da mecânica.
Below, apresentamos o princípio da invariância generalizada e a correspondente representação do momento generalizado do sistema, as equações da mecânica relativista e quântica , dão as soluções dos problemas de movimento de carga em um campo elétrico constante, os problemas para uma partícula em um poço potencial e a passagem de uma partícula por uma barreira potencial, os problemas de movimento em um campo exponencial (Morse), os problemas de partícula carregada em um campo magnético, e também os problemas de um átomo de hidrogênio são dados.




