Interpretando os coeficientes de regressão linear
>
Aprenda a interpretar correctamente os resultados da regressão linear – incluindo casos com transformações de variáveis
Agora hoje em dia existe uma infinidade de algoritmos de aprendizagem de máquinas que podemos tentar encontrar o melhor ajuste para o nosso problema particular. Alguns dos algoritmos têm interpretação clara, outros funcionam como uma caixa preta e podemos usar abordagens como LIME ou SHAP para derivar algumas interpretações.
Neste artigo, eu gostaria de focar na interpretação dos coeficientes do modelo de regressão mais básico, nomeadamente a regressão linear, incluindo as situações em que as variáveis dependentes/independentes foram transformadas (neste caso estou a falar da transformação de log).
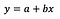
Presumo que o leitor esteja familiarizado com a regressão linear (se não houver muitos bons artigos e posts Médias), por isso vou focar-me apenas na interpretação dos coeficientes.
A fórmula básica da regressão linear pode ser vista acima (omiti os resíduos de propósito, para manter as coisas simples e directas). Na fórmula, y denota a variável dependente e x é a variável independente. Para simplificar, vamos assumir que é uma regressão univariada, mas os princípios obviamente também se mantêm para o caso multivariado.
Para colocar em perspectiva, digamos que depois de encaixar o modelo que recebemos:
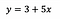
Intercept (a)
Dividirei a interpretação da intercepção em dois casos:
- x é contínuo e centrado (subtraindo a média de x de cada observação, a média de x transformado torna-se 0) – média y é 3 quando x é igual à média da amostra
- x é contínuo, mas não centrada – média y é 3 quando x = 0
- x é categórica – média y é 3 quando x = 0 (desta vez indicando uma categoria, mais sobre isto abaixo)
Coeficiente (b)
- x é uma variável contínua
Interpretação: um aumento unitário em x resulta em um aumento médio de y em 5 unidades, todas as outras variáveis mantidas constantes.
- x é uma variável categórica
Isso requer um pouco mais de explicação. Digamos que x descreve gênero e pode tomar valores (‘masculino’, ‘feminino’). Agora vamos convertê-la em uma variável dummy que toma valores 0 para homens e 1 para mulheres.
Interpretação: y médio é maior em 5 unidades para mulheres do que para homens, todas as outras variáveis mantidas constantes.
Modelo a nível de log
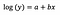
Tipicamente utilizamos a transformação de log para extrair os dados periféricos de uma distribuição positivamente enviesada para mais perto da maior parte dos dados, a fim de tornar a variável normalmente distribuída. No caso da regressão linear, um benefício adicional do uso da transformação de log é a interpretabilidade.
Como antes, digamos que a fórmula abaixo apresenta os coeficientes do modelo ajustado.
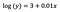
Intercept (a)
Interpretação é semelhante como no caso da vanilla (nível de nível), no entanto, precisamos tomar o expoente da intercepção para interpretação exp(3) = 20,09. A diferença é que este valor representa a média geométrica de y (ao contrário da média aritmética no caso do modelo em nível de nível).
Coeficiente (b)
Os princípios são novamente semelhantes ao modelo em nível de nível quando se trata de interpretar variáveis categóricas/numéricas. Analogamente à intercepção, precisamos pegar o expoente do coeficiente: exp(b) = exp(0.01) = 1.01. Isto significa que um aumento unitário em x causa um aumento de 1% na média (geométrica) y, todas as outras variáveis mantidas constantes.
Duas coisas que vale a pena mencionar aqui:
- Existe uma regra quando se trata de interpretar coeficientes de um modelo deste tipo. Se abs(b) < 0,15 é bastante seguro dizer que quando b = 0,1 vamos observar um aumento de 10% em y para uma mudança de unidade em x. Para coeficientes com valor absoluto maior, é recomendado calcular o expoente.
- Quando se lida com variáveis no intervalo (como uma porcentagem) é mais conveniente para a interpretação primeiro multiplicar a variável por 100 e depois encaixar no modelo. Desta forma a interpretação é mais intuitiva, pois aumentamos a variável em 1 ponto percentual ao invés de 100 pontos percentuais (de 0 a 1 imediatamente).
modelo de nível de log
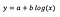
Vamos supor que depois de encaixarmos o modelo recebemos:

A interpretação da intercepção é a mesma que no caso do modelo de nível.
Para o coeficiente b – um aumento de 1% em x resulta num aumento aproximado na média y por b/100 (0,05 neste caso), todas as outras variáveis mantidas constantes. Para obter a quantidade exata, seria necessário tomar b× log(1,01), que neste caso dá 0,0498.
log-log modelo
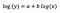
Vamos assumir que depois de encaixarmos o modelo que recebemos:
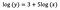
Só novamente foco na interpretação de b. Um aumento em x por 1% resulta em um aumento de 5% na média (geométrica) y, todas as outras variáveis mantidas constantes. Para obter a quantidade exata, precisamos tomar
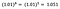
que é ~5,1%.
Conclusões
Espero que este artigo tenha dado uma visão geral de como interpretar os coeficientes de regressão linear, incluindo os casos em que algumas das variáveis foram log-transformadas. Como sempre, qualquer feedback construtivo é bem-vindo. Você pode me contactar no Twitter ou nos comentários.




