Introdução à Probabilidade: Artigos e Vídeos com Soluções!

admin 0 Comments Articles

Introdução à Probabilidade: Artigos e Vídeos com Soluções!

Rolar os dados, encontrar um lugar de estacionamento, ganhar nas cartas; Estas são apenas algumas situações em que você pode querer encontrar as probabilidades de um evento acontecer. Se você quer saber como encontrar a probabilidade, primeiro você tem que descobrir que tipo de pergunta você tem. Por exemplo, como você encontra as probabilidades de um evento acontecer é diferente de encontrar as probabilidades dos membros do grupo que escolhem a mesma coisa.

Algumas probabilidades são fáceis de identificar, como encontrar probabilidades de lançamento de dados ou escolher a partir de um baralho de cartas.

Questões que envolvem o teorema binomial também são fáceis de identificar. Nestes tipos de experimentos, os únicos resultados possíveis de um evento são “Sucesso” ou “Fracasso”: como sim/não, cabeça/cavalo ou preto/branco.

Outros tipos de perguntas que você pode encontrar envolvem pessoas, como:

• Selecionar uma pessoa de um grupo ou comitê.
• Probabilidade de um grupo escolher a mesma coisa.

Eventos

Você quer encontrar a probabilidade de um evento simples acontecer? Como se estivesse chovendo, ou encontrar um lugar de estacionamento no centro da cidade? Veja:
Probabilidade de um evento simples acontecer.
Por outro lado, se você quiser exatamente o oposto, veja:
Como descobrir a probabilidade de um evento NÃO acontecer.

A sua pergunta sobre um evento que está acontecendo, tem outro evento? Como as probabilidades de encontrar um lugar de estacionamento, dado que é dia de jogo, ou de encontrar um certo brinquedo popular na Sexta-feira Negra? Se sim, confira:

• Probabilidades de um evento, dado outro evento.
• Dois eventos ocorrendo juntos.

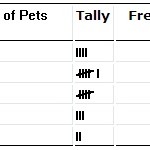
Uma tabela de distribuição de frequência.

Distribuições de frequência

Você tem uma distribuição de frequência para trabalhar? Ou você é capaz de fazer uma tabela de distribuição de freqüência com seus dados fornecidos? Por exemplo, você tem x número de itens com um certo traço. Distribuição de freqüência de probabilidade.

Introdução à Probabilidade: Artigos e Vídeos.

1. Permutações e Combinações: Como resolver problemas
2. Probabilidade de problemas: Resolva-os da maneira fácil!
3. Probabilidade de a e b.
4. Regra Total de Probabilidade.
5. Problemas do Teorema de Bayes: Easy Solution Steps.
6. Probabilidade anterior (incluindo Uninformative e Conjugate).
7. Como fazer uma distribuição de probabilidade a partir de dados.
8. Como encontrar a Probabilidade de Seleccionar uma Pessoa de um Grupo ou Comité.
9. Como encontrar a Probabilidade de um Evento NÃO Acontecendo.
10. Distribuição de Frequência de Probabilidade.
11. Como encontrar a Probabilidade de um Evento Simples Acontecendo.
12. Evento Aleatório: Probabilidade Dada uma Porcentagem.
13. Como Encontrar a Probabilidade de Membros do Grupo Escolhendo a Mesma Coisa.
14. Como Encontrar a Probabilidade de Dois Eventos Dependentes Ocorrendo Juntos.
15. Como Encontrar a Probabilidade de um Evento Ocorrendo, Dado Outro Evento.
16. Como usar uma Árvore de Probabilidade (Árvore de Decisão) para calcular probabilidades.
17. Como encontrar a Probabilidade de Desenhar um Cartão de um Deck.
18. Como descobrir se algo é um Evento Mutualmente Exclusivo.
19. Como dizer a diferença entre Eventos Dependentes e Independentes.
20. Probabilidade: Rolagem de Dados.
21. Como desenhar um diagrama Venn.
22. Como criar um diagrama Euler.
23. 5 escolha 3: como resolver combinações.
24. Como usar o princípio fundamental de contagem.
25. Como encontrar o valor esperado para uma variável aleatória discreta.

Introdução à Probabilidade: Definições

• Probabilidade Axiomática.
• A Lei de Benford
• O que é uma Experiência Binomial?
• Taxas de Base e a Taxa Base de Falácia
• Pontuações de Brier
• Exaustivo Coletivamente
• O que são Combinações?
• Eventos Complementares.
• Expectativa Condicional
• Qual é a Freqüência Relativa Condicional?

>

• Aditividade Contável

>

• Empty Set

>

• Probabilidade Epistémica

>

• Espaços de Eventos.

>

• O que é Probabilidade Experimental?

>

• Distribuições de Probabilidade Juntas.

>

• Distribuição Limitada.
• Máxima Estimativa de Probabilidade
• Propriedade sem Memória.
• Método Monte Carlo.
• Problema do Salão de Morte
• O que é um Evento Mutualmente Exclusivo?
• O que é um Evento Mutualmente Inclusivo?

>

• Independente mútuo e independente de pares.

>

• Qual é a regra de multiplicação?

>

• Equilíbrio de Nash

>

• Conjunto não vazio

>

• Problemas de prática normal de probabilidades.

>

• O que é um Pote de Probabilidade Normal?
• Probabilidade Objetiva

>

• Qual é a Razão de Probabilidade?
• Análise Preditiva

>

• O que é uma Tabela de Distribuição de Probabilidade?
• Medida de Probabilidade
• O que é um Espaço de Probabilidade?
• Vetores de Probabilidade
• O que são Espaços de Amostra?
• Modelos Estocásticos.
• O que é uma Probabilidade Subjetiva?
• O que é Probabilidade Teórica?
• O que é um Modelo de Urna?

Calculadores.

• Calculadora de permutações on-line e calculadora de combinações.

Fórmulas de Probabilidade / Regras de Probabilidade

Uma das coisas mais desconfortáveis que os alunos não gostam nas fórmulas é a falta delas em probabilidade e estatística. Existem alguns grampos, incluindo algumas notações imperdíveis:

Intervalo de Probabilidade
0 ≤ P(A) ≤ 1
Este indica que a probabilidade de um evento está entre zero e 100% (como uma casa decimal, ou seja, 0 e 1). Você vai querer se lembrar desta regra ao adicionar ou multiplicar probabilidades de eventos. Se a sua resposta for superior a 100%, isso é uma pista que você pode ter feito algo errado.

Regra de Eventos Complementares
P(AC) + P(A) = 1
Eventos complementares acontecem quando há apenas dois resultados, como atirar uma moeda ao ar. Rolar um dado para ver se você teria seis também é complementar; os dois únicos resultados são seis (uma chance de 1/6) ou não seis (5/6 chances). As duas probabilidades devem somar até 1.
Você também pode ver esta fórmula escrita assim:
p(A) + p(A’) = 1
que pode ser rearranjada algebricamente para ler:
p(A’) = 1 – p(A).
Todas as três fórmulas são equivalentes: qual terminologia (A’ ou Ac) é usada cabe ao autor do livro didático e ao professor. Pessoalmente, eu prefiro A’, que eu chamo de “não A”. A probabilidade de “não A”, penso eu, é mais fácil de compreender do que “o complemento” (ou um evento acontece, ou não acontece).

Regra da adição
P(A∪B) = P(A) + P(B) – P(A∩B)
onde ∪ é a união e ∩ é a intersecção.
O que isto está a dizer (em inglês!) é a probabilidade do evento A OU evento B acontecer (ou ambos ao mesmo tempo) é:

• A probabilidade do evento A acontecer por si mesmo,
• Plus a probabilidade do evento B acontecer por si mesmo,
• Plus a probabilidade dos dois eventos acontecerem ao mesmo tempo.

Se você tiver eventos mutuamente exclusivos, então P(A∩B) não pode acontecer (os eventos não podem acontecer juntos), então a fórmula se torna:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Eventos A e B são desjuntos se:
P(A∩B) = 0
Esta é apenas outra forma de dizer que os eventos são mutuamente exclusivos. Eles não podem acontecer ao mesmo tempo.

A fórmula relacionada é P((A∪B)c) ou, equivalentemente ((A∪B)’). Em inglês, isto diz “not the union” (não a união). Para resolver isso, descubra a união e tire o resultado de 1 (porque a probabilidade dos eventos acontecerem ou não acontecerem deve somar 1).

Probabilidade Condicional
P(A|B) = P(A∩B) / P(B)
O símbolo “|” significa “dado que”. Em outras palavras, a probabilidade de ocorrência do evento B, dado que o evento A acontece. Para exemplos de como usar a fórmula, veja: conditional probability.

Bayes Formula
P(A|B) = P(B|A) – P(A)/ P(B)
Teorema de Bayes é uma forma de calcular a probabilidade condicional, embora seja um pouco mais matizada. Em poucas palavras, ele lhe dá a probabilidade real de um evento dado informações sobre testes. Por exemplo, qual é a probabilidade de você ter câncer se o seu teste médico for positivo (resposta = muito menor do que você pensa). Para alguns exemplos, veja: Exemplos do Teorema Bayes e Distribuições Posteriores / Probabilidades Posteriores.

Eventos independentes
Eventos A e B são independentes se um deles não afeta a probabilidade do outro. Também se diz que os eventos são independentes se a seguinte equação for verdadeira.
P(A∩B) = P(A) – P(B).
Esta equação é derivada da regra de multiplicação, que diz que P(A∩B) = P(A) * P(B|A). Como sabemos que P(B|A) = P(B) para eventos independentes, podemos substituir P(B|A) por P(B), dando-nos a fórmula.

Algumas Notas sobre Regras de Probabilidade

Estatistica é sobre o acaso e o “ballparking”, não absolutos e a “resposta certa”. Basta olhar para qualquer sondagem Gallup – eles raramente estão mais de 90% confiantes de que têm a “resposta certa”. Há técnicas que você pode usar para descobrir as probabilidades (como multiplicar duas probabilidades juntas, ou adicioná-las). No entanto, além talvez da tabela de distribuição binomial e das fórmulas acima (que na vida real, não são muito usadas), não existem realmente fórmulas de probabilidade que você possa aplicar facilmente. Você tem que reverter para aquele velho básico da escola primária, a lógica (você se lembra disso… ela estava lá bem antes deles começarem a testar a lógica padronizada fora de você).

As três Regras das fórmulas de probabilidade:

1. Não há regras (bem, muito poucas, excepto as listadas acima).
2. Usa lógica, não equações.
3. Existem muitas, muitas formas diferentes de chegar à resposta – nenhuma das quais usa realmente fórmulas.

Há uma pergunta que chegou na minha caixa de entrada esta manhã que aborda as probabilidades:

“Se você estivesse tentando coletar 6 cartões de beisebol que vieram em pacotes de puffs de queijo, assumindo que eles são distribuídos uniformemente quantos pacotes de puffs de queijo você esperaria comprar antes de ter todos os 6 cartões?”

O primeiro passo para resolver este problema é perceber que você não pode procurar a resposta em uma tabela. Para resolvê-lo, você tem que pensar como uma criança.

Card# 1:Você tem 8 anos de idade novamente, entrando numa loja com dinheiro suficiente para comprar um saco de folhados de queijo. Você espera coletar todos os 5 cartões de beisebol, mas ainda não tem nenhum. Quais são as chances de você comprar um saco e obter um cartão que você quer?

A resposta, é claro, é 100%. Compre sua primeira sacola, e você tem 100% de chance de ter um cartão que você quer.

Cartão# 2: Agora fica um pouco mais complicado. Voltas à loja para obteres o cartão#2. Mas como já tens o cartão nº 1, Mickey Mantle. Você não o quer de novo, mas há uma chance de 1/5 de você poder pegá-lo (e portanto 4/5 de chance você não vai). Quantos sacos de folhados de queijo você terá que comprar para conseguir a carta #2 se torna um problema de proporção. Você pode descobrir na sua cabeça, mas se você quiser modelá-lo matematicamente, você tem que configurar a equação. Se um saco de folhados de queijo te dá 80% de chance de conseguir o cartão que você quer, quantos sacos você precisa comprar para ter 100% de chance?

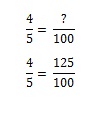
Para conseguir 100% você precisaria comprar 1,25 sacos.

Card# 3:As chances começam a ficar mais difíceis. Você tem 60% de chances de conseguir o terceiro cartão de beisebol, e você terá que comprar 1,667 sacas para conseguir esse terceiro cartão.

Card# 4:As chances começam a ficar um pouco desanimadoras. Você tem 40% de chance de conseguir o quarto cartão de beisebol, e terá que comprar 2,5 sacos para conseguir aquele terceiro cartão.

Card# 5:As probabilidades estão contra você. Você tem 20% de chances de conseguir o último cartão, e terá que comprar 5 sacolas para conseguir aquele terceiro cartão.

Então a quantidade total de sacolas que você terá que comprar é igual a:
1 + 1,25 + 1,667 + 2,5 + 5
Mas espere! (E é aqui que entra um pouco de lógica). Você não pode entrar em uma loja e comprar 1,25 sacos de puffs de queijo, então você terá que arredondar para cima. A equação torna-se:
1 + 2 + 2 + 3 + 5 = 13 sacos.

Um ponto importante para as fórmulas: lembre-se que nada é absoluto. Estou razoavelmente confiante de que se você comprasse 13 sacos de folhados de queijo e assumindo que os cartões são distribuídos uniformemente, você receberia todos os 5 cartões. Mas….a probabilidade é sobre o acaso, e pode ser apenas o seu azar de conseguir o mesmo cartão 10 vezes seguidas (lembro-me disso acontecer comigo quando era criança). Mas pode haver outra explicação para o seu “azar”, e é que as empresas querem que você compre o maior número possível de sacolas, então elas tentarão fazer com que as probabilidades funcionem a seu favor. Mesmo que os cartões sejam distribuídos uniformemente, a empresa poderia enviar malas com os cartões nº 1, nº 2, e nº 3 para uma loja (portanto, te enrolando fazendo com que você colete mais da metade dos cartões) e nº 4 e nº 5 para outra loja.

Que outras formas você pode pensar que os fabricantes podem virar as chances a seu favor?

Probabilidade de um Grupo Escolhendo a Mesma Coisa

As questões de probabilidade podem ser divididas em diferentes tipos. Quando lhe é pedido para encontrar a probabilidade de um grupo escolher a mesma coisa, você está considerando as ações de membros aleatórios de um grupo (pode ser tão pequeno quanto um comitê ou pode ser tão grande quanto a população dos Estados Unidos).
Estas questões de probabilidade dão-lhe um grupo, e pede-lhe para calcular a probabilidade de um evento ocorrer para um certo número de membros aleatórios dentro desse grupo.

Probabilidade de um grupo escolher a mesma coisa : Passos

Problema da amostra: Há 200 pessoas numa feira de livros. 159 delas vão comprar pelo menos um livro. Se você pesquisar 5 pessoas aleatórias saindo da porta, qual é a probabilidade de todas elas terem comprado pelo menos um livro?

Qual é a probabilidade de um grupo comprar pelo menos um livro?

Passo 1: Converta os dados na pergunta para uma fração. Por exemplo, a frase “159 pessoas em 200” pode ser convertida para: 159/200.

Passo 2: Multiplique a fração por si só. Repita para muitos itens aleatórios (ou seja, pessoas), no entanto, são escolhidos. Em nosso exemplo, temos 5 pessoas pesquisadas, então queremos:

159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Esse é como encontrar a Probabilidade de um Grupo Escolher a Mesma Coisa!

Tip: Pode ser mais fácil converter a fração em uma casa decimal antes de multiplicar. Neste caso, 159/200 = 0.795.

Cheque nosso canal no YouTube para mais ajuda e dicas sobre estatísticas! Nós temos vídeos para os problemas mais comuns que você provavelmente encontrará. Mais vídeos para usar o Excel em estatísticas > tudo desde fazer gráficos de barras básicos até resolver problemas complexos de análise de dados.

——————————————————————————

Need ajuda com um trabalho de casa ou pergunta de teste? Com o Chegg Study, você pode obter soluções passo-a-passo para suas perguntas de um especialista na área. Seus primeiros 30 minutos com um tutor do Chegg são grátis!