Början av algebra
Lärandemål
- Plotta ordnade par
- Identifiera komponenterna i koordinatplanet
- Plotta ordnade par på koordinatplanet
- Identifiera kvadranter på koordinatplanet
- Identifiera de fyra kvadranterna på ett koordinatplan
- Givet ett ordnat par, bestäm dess kvadrant
Koordinatplanet utvecklades för flera hundra år sedan (1637, för att vara exakt) och förfinades av den franske matematikern René Descartes. Till hans ära kallas systemet ibland för det cartesiska koordinatsystemet. Koordinatplanet kan användas för att plotta punkter och grafera linjer. Detta system gör det möjligt för oss att beskriva algebraiska samband på ett visuellt sätt och hjälper oss också att skapa och tolka algebraiska begrepp.
Koordinatplanets komponenter
Du har troligen använt ett koordinatplan tidigare. Har du till exempel någonsin använt ett rutnätsöverlägg för att kartlägga ett objekts position? (Detta görs ofta med vägkartor också.)

Denna ”karta” använder ett horisontellt och vertikalt rutnät för att förmedla information om ett objekts läge. Lägg märke till att bokstäverna A-F är listade längs den övre kanten och att siffrorna 1-6 är listade längs den vänstra kanten. Den allmänna platsen för ett objekt på denna karta kan hittas genom att använda bokstaven och numret för dess rutnätruta. Du kan till exempel hitta föremålet som finns på rutan ”4F” genom att föra fingret längs det horisontella till bokstaven F och sedan rakt ner så att du är i linje med 4. Du hittar en blå skiva som finns på denna plats på kartan.
Koordinatplanet har liknande element som det rutnät som visas ovan. Den består av en horisontell axel och en vertikal axel, tallinjer som skär varandra i rät vinkel. (De är vinkelräta mot varandra.)
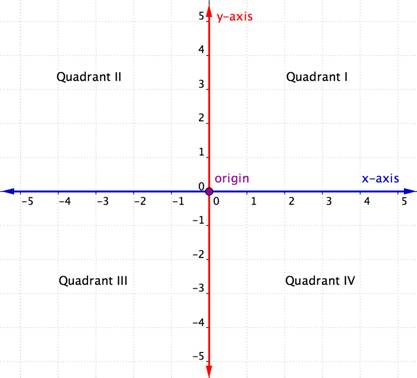
Den horisontella axeln i koordinatplanet kallas x-axeln. Den vertikala axeln kallas y-axeln. Den punkt där de två axlarna skär varandra kallas ursprunget. Ursprunget ligger vid 0 på x-axeln och 0 på y-axeln.
Lokaliseringar på koordinatplanet beskrivs som ordnade par. Ett ordnat par talar om en punkts läge genom att relatera punktens läge längs x-axeln (det första värdet i det ordnade paret) och längs y-axeln (det andra värdet i det ordnade paret).
I ett ordnat par, till exempel (x, y), kallas det första värdet för x-koordinat och det andra värdet för y-koordinat. Observera att x-koordinaten anges före y-koordinaten. Eftersom ursprunget har x-koordinaten 0 och y-koordinaten 0 skrivs dess ordnade par (0, 0).
Konsultera punkten nedan.

För att identifiera platsen för denna punkt börjar du vid ursprunget (0, 0) och rör dig till höger längs x-axeln tills du befinner dig under punkten. Titta på etiketten på x-axeln. 4 anger att du från origo har förflyttat dig fyra enheter till höger längs x-axeln. Detta är x-koordinaten, det första talet i det ordnade paret.
Från 4 på x-axeln förflyttar du dig upp till punkten och lägger märke till det tal som den ligger i linje med på y-axeln. 3 anger att du, efter att ha lämnat x-axeln, har färdats 3 enheter uppåt i vertikal riktning, dvs. y-axelns riktning. Detta tal är y-koordinaten, det andra talet i det ordnade paret. Med en x-koordinat på 4 och en y-koordinat på 3 har du det ordnade paret (4, 3).
Låt oss titta på ett annat exempel.
Exempel
Beskriv punkten som visas som ett ordnat par.

Beskriv punkten som visas som ett ordnat par
Plottning av punkter i koordinatplanet
Nu när du vet hur man använder x- och y-axeln kan du också plotta ett ordnat par. Kom bara ihåg att båda processerna börjar vid ursprunget – början! Exemplet som följer visar hur du kan grafera det ordnade paret (1,3).
Exempel
Plottar punkten (1, 3).
I det föregående exemplet var både x- och y-koordinaterna positiva. När en (eller båda) av koordinaterna i ett ordnat par är negativa måste du förflytta dig i den negativa riktningen längs en eller båda axlarna. Tänk på exemplet nedan där båda koordinaterna är negativa.
Exempel
Plotta punkten (-4,-2).

X-koordinaten är -4 eftersom den kommer först i det ordnade paret. Börja vid origo och flytta 4 enheter i negativ riktning (vänster) längs x-axeln.
Y-koordinaten är -2 eftersom den kommer som nummer två i det ordnade paret. Flytta nu 2 enheter i negativ riktning (nedåt). Om du tittar över till y-axeln bör du vara uppradad med -2 på den axeln.
Steggen för att rita en punkt sammanfattas nedan.
Steggen för att rita ett ordnat par (x, y) i koordinatplanet
- Bestäm x-koordinaten. Börja vid ursprunget och förflytta dig horisontellt, i x-axelns riktning, det avstånd som ges av x-koordinaten. Om x-koordinaten är positiv flyttas du till höger; om x-koordinaten är negativ flyttas du till vänster.
- Bestäm y-koordinaten. Börja vid x-koordinaten och förflytta dig vertikalt, i y-axelns riktning, det avstånd som ges av y-koordinaten. Om y-koordinaten är positiv, förflyttar du dig uppåt; om y-koordinaten är negativ, förflyttar du dig nedåt.
- Teckna en punkt på slutplatsen. Märk punkten med det ordnade paret.
Plotta punkter på koordinatplanet
Identifiera kvadranter och använd dem för att plotta punkter
Koordinatplanets skärande x- och y-axlar delar upp det i fyra delar. Dessa fyra sektioner kallas kvadranter. Kvadranter benämns med hjälp av de romerska siffrorna I, II, III och IV som börjar med den övre högra kvadranten och rör sig moturs.
Ordnade par inom en viss kvadrant delar vissa egenskaper. Titta på varje kvadrant i grafen nedan. Vad lägger du märke till om tecknen på x- och y-koordinaterna för punkterna inom varje kvadrant?
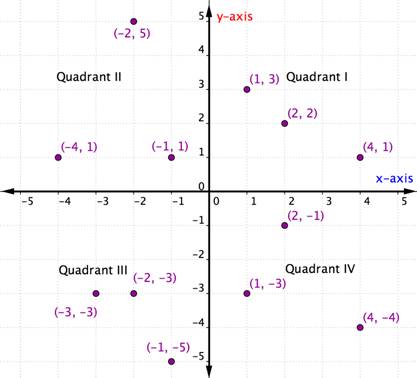
Inom varje kvadrant är tecknen på x-koordinaterna och y-koordinaterna för varje ordnat par desamma. De följer också ett mönster som beskrivs i tabellen nedan.
| Kvadrant | Allmän form för punkt i denna kvadrant | Exempel | Beskrivning |
|---|---|---|---|
| I | (+,+) | (5,4) | Gå från origo längs x-axeln i positiv riktning (höger) och längs y-axeln i positiv riktning (uppåt). |
| II | (-,+) | (-5,4) | Med utgångspunkt från ursprunget ska du gå längs x-axeln i negativ riktning (vänster) och längs y-axeln i positiv riktning (uppåt). |
| III | (-,-) | (-5,-4) | Gå längs x-axeln i negativ riktning (vänster) och längs y-axeln i negativ riktning (nedåt) med utgångspunkt från origo. |
| IV | (+,-) | (5,-4) | Gå längs x-axeln i positiv riktning (höger) och längs y-axeln i negativ riktning (nedåt) med utgångspunkt från ursprunget. |
När du känner till kvadranterna i koordinatplanet kan du bestämma kvadranten för ett ordnat par utan att ens grafera det genom att titta på diagrammet ovan. Här är ett annat sätt att tänka på det.
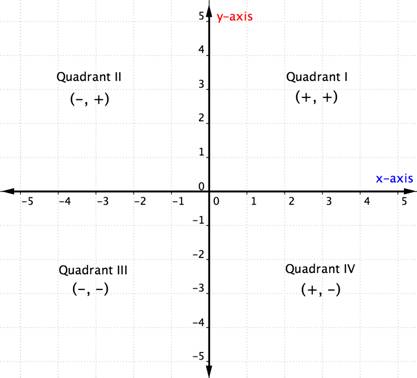
Exemplet nedan beskriver hur man kan bestämma kvadrantens läge för en punkt bara genom att tänka på tecknen på dess koordinater. Att tänka på kvadrantläget innan du plottar en punkt kan hjälpa dig att undvika misstag. Det är också användbar kunskap för att kontrollera att du har plottat en punkt korrekt.
Exempel
I vilken kvadrant ligger punkten (-7,10)?
Exempel
I vilken kvadrant ligger punkten (-10,-5)?
Vad händer om ett ordnat par har en x- eller y-koordinat på noll? Exemplet nedan visar grafen för det ordnade paret (0,4).
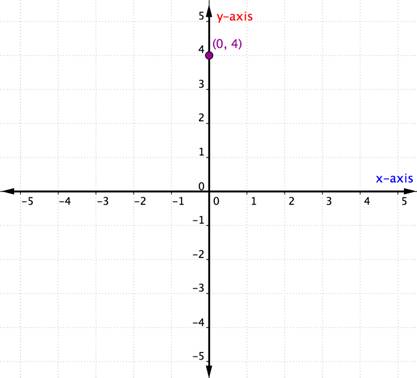
En punkt som ligger på en av axlarna anses inte ligga i en kvadrant. Den ligger helt enkelt på en av axlarna. När x-koordinaten är 0 ligger punkten på y-axeln. På samma sätt kommer varje punkt som har y-koordinaten 0 att ligga på x-axeln.
Identifiera kvadranter och använd dem för att plotta punkter
Sammanfattning
Koordinatplanet är ett system för att grafera och beskriva punkter och linjer. Koordinatplanet består av en horisontell (x-) axel och en vertikal (y-) axel. Skärningen av dessa linjer skapar ursprunget, som är punkten (0,0). Koordinatplanet är uppdelat i fyra kvadranter. Tillsammans gör dessa egenskaper hos koordinatsystemet det möjligt att grafiskt representera och kommunicera om punkter, linjer och andra algebraiska begrepp.





