Lexikon för centrifugalpumpar
Tryckförlust beror på väggfriktion i alla typer av rörledningar och på lokalt flödesmotstånd, t.ex. i ventiler och kopplingar (se även Tryckförlust).
Rekommenderade flödeshastigheter
- För kallt vatten:
Sugledning 0.7-1,5 m/s
Utloppsledning 1,0-2,0 m/s - För varmvatten:
Sugledning 0,5-1,0 m/s
Utloppsledning 1,5-3,5 m/s
Ekvationen för tryckhöjdsförlusten för ett flöde i en rak ledningssträcka med cirkulärt tvärsnitt är:
λ Rörfriktionsfaktor
L Rörlängd i m
d Rörets innerdiameter i m
v Flödeshastighet i ett tvärsnitt i m/s
(= 4 Q / π d2 med Q i m3 /s)
g Acceleration på grund av gravitationen i m/s2
se fig. 1 och 4 Huvudförlust
Rörfriktionsfaktorn har fastställts experimentellt. Den är endast beroende av flödestillståndet hos den behandlade vätskan och av den relativa ojämnheten (d/k) hos de rör genom vilka vätskan strömmar. För icke-cirkulära rörtvärsnitt gäller den ekvivalenta diametern i fluidmekaniska termer (d):
A Tvärsnitt i m2
U Vattentäta tvärsnittets omkrets i m
(den fria ytan i en öppen kanal beaktas inte)
Flödestillståndet bestäms av Reynoldstalet (Re) i enlighet med affinitetslagarna. Följande gäller för cirkulära rör:
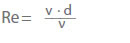
v Flödeshastighet i ett tvärsnitt i m/s
(= 4 Q / π d2 med Q i m3/s)
ν Kinematisk viskositet i m2/s
(för vatten vid 20 °C: 1.00 – 10 – 6 m2/s)
d Rörets innerdiameter i m
Se fig. 4 Huvudförlust
För hydrauliskt släta rör, t.ex. släta dragna metall- eller plaströr (t.ex. PE eller PVC), eller vid laminärt flöde, kan rörets friktionsfaktor (λ) beräknas. För laminärt flöde i ett rör med ett Reynoldstal som är mindre än 2320 är rörfriktionsfaktorn oberoende av ojämnheten:
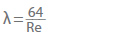
Om flödet är turbulent, eller om Reynoldstalet är högre än 2320, kan rörfriktionsfaktorn i hydrauliskt släta rör representeras av en empirisk ekvation enligt Eck (på grund av att avvikelserna är mindre än 1 % om Reynoldstalet är lägre än 108).
Rörfriktionsfaktorn (λ) beror också på ytterligare en dimensionslös parameter, nämligen på den relativa råheten hos rörets inre yta (d/k). Båda måste anges i samma enhet (t.ex. mm).
Se fig. 1 Huvudförlust
(k) är den genomsnittliga absoluta ojämnheten hos rörets inre yta, för vilken ungefärliga värden finns tillgängliga beroende på material och tillverkningsprocesser. Se fig. 2 Huvudförlust
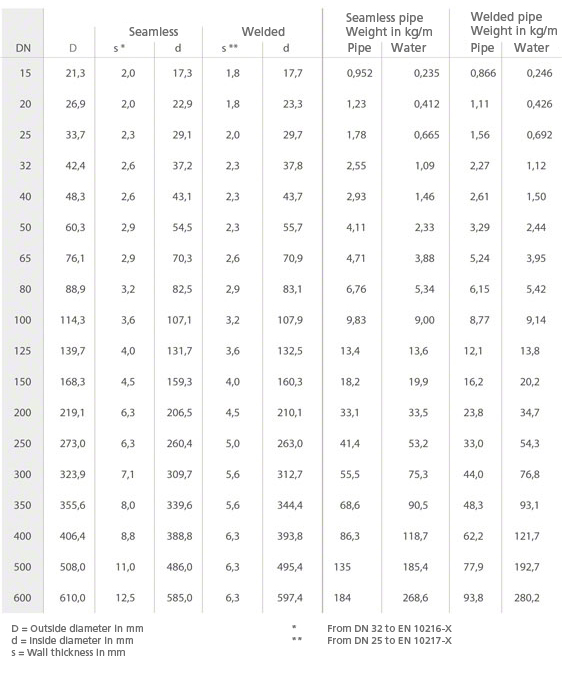Fig. 2 Huvudförlust: Uppskattningar av genomsnittliga höjder från topp till dal k (absolut grovhet) för rör
Ovanför gränskurvan är rörets friktionsfaktor (λ) enbart beroende av rörets relativa grovhet (d/k). Se fig. 1 Fallhöjdsförlust
Följande empiriska ekvation av Moody kan användas för detta område:
För praktisk användning visas fallhöjdsförlusten (HL) per 100 m rakt stålrör i diagrammet som funktion av flödeshastigheten (Q) och rörets innerdiameter (d).
Se fig. 3 Fallhöjdsförlust
Värdena gäller endast för kallt, rent vatten eller för vätskor med samma kinematiska viskositet, för helt fyllda rör och för en absolut råhet på rörets inre yta på k = 0.05 mm.
Dimensioner, vikter, vattenfyllning för nya sömlösa eller längsgående svetsade stålrör
Se bilaga, Huvudförlust, fig. 4
Effekten av en ökad ytråhet k kommer att demonstreras i det följande för en ofta använd uppsättning parametrar (nominell diameter DN = 50 till 300, flödeshastighet v = 0,8 till 3,0 m/s). Se fig. 3 Huvudförlust
Den ljusblå regionen motsvarar den likadant markerade regionen för en absolut genomsnittlig ytjämnhet k = 0,05 mm.
Se fig. 1 Huvudförlust
För en ökad ytjämnhet med en faktor 6 (lätt inkrusterat gammalt stålrör med k = 0,30 = 300 μm (0.30 mm) är rörens friktionsfaktorer (och de tillhörande proportionella fallhöjdsförlusterna) i det mörkblå området endast 25-60 % högre än tidigare.
Se fig. 1 Fallhöjdsförlust
För avloppsrör måste man ta hänsyn till den ökade ojämnhet som orsakas av nedsmutsning. För rör som utsätts för extrem inkrustering kan den faktiska fallhöjdsförlusten endast bestämmas experimentellt. Avvikelser från den nominella diametern förändrar tryckförlusten avsevärt, eftersom rörets innerdiameter ingår i ekvationen till femte potensen.
En minskning av innerdiametern med 5 % leder till exempel till en ökning av tryckförlusten med så mycket som 30 %. Det är därför viktigt att innerdiametern inte bara ersätts med den nominella diametern i beräkningarna.
Huvudförlusterna i plaströr eller slätdragna metallrör är mycket låga tack vare de släta rörytorna. De fastställda tryckförlusterna gäller för vatten vid 10 °C. Vid andra temperaturer måste förlusten för plaströr multipliceras med en specificerad temperaturkorrigeringsfaktor för att ta hänsyn till deras större termiska expansion. För avloppsvatten eller annat obehandlat vatten bör ytterligare 20-30 % fallhöjdsförlust beaktas för eventuella avlagringar.
Fallhöjdsförluster för plaströr och släta dragna metallrör
Se bilaga, Fallhöjdsförlust, fig. 5
Huvudförluster i ventiler och rördelar
Huvudförlusten (HL) i ventiler och rördelar ges av:
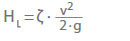
ζ Förlustkoefficient
Se fig. 6-12 Huvudförlust
v Flödeshastighet i en karakteristisk tvärsnittsarea A
(t.ex. vid munstycket) i m/s
g Gravitationsacceleration 9,81 m/s2
Fig. 6 Huvudförlust: Schematisk bild av ventilkonstruktioner
Fig. 11 Head loss: Inverkan på förlustkoefficienten ζ av att avrunda den inre och yttre sidan av armbågar i fyrkantiga kanaler
Fig. 12 Head loss: Förlustkoefficienter ζ för fjärils-, globe- och grindventiler beroende på öppningsgrad
De förluster som kan hänföras till uträtning av flödesstörningar över en rörlängd motsvarande 12 x DN nedströms ventilen inkluderas i förlustkoefficienterna i enlighet med riktlinjen VDI/VDE 2173. Värdena gäller för ventiler som har ett jämnt tillrinningsflöde, är helt öppna och drivs med kallt vatten. Beroende på flödesförhållandena vid in- och utlopp, ventilmodellerna och utvecklingsmålen (dvs. billiga eller energisnåla ventiler) kan förlustvärdena variera dramatiskt. Se bilaga, Head loss, fig. 7
Ofta används kv-värdet i stället för förlustkoefficienten (ζ) vid beräkning av tryckförlusten för vatten i ventiler:
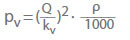
Kv-värdet är den flödeshastighet i m3 /h som skulle bli resultatet av en tryckförlust pv = 1 bar genom ventilen för kallt vatten. Det beskriver sambandet mellan tryckförlusten (pL) i bar och flödeshastigheten (Q) i m3/h. Omvandling till flödeskoefficient ζ för kallt vatten:
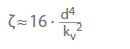
d Ventilens referensdiameter (nominell) i cm
För beräkning av fallhöjdsförluster i armaturer kräver förgreningsarmaturer och adaptrar en annan metod. Se figurerna 9 och 10 Huvudförlust
Fig. 9 Huvudförlust: Förlustkoefficienter ζ för armaturer 
Fig. 10: Huvudförlust:
För alla kopplingar måste man skilja mellan två former av tryckförlust:
- Ireversibla tryckförluster (tryckminskning)
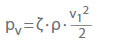
pv Tryckförlust i Pa
ζ Förlustkoefficient
ρ Densitet i kg/m3
v Flödeshastighet i ett tvärsnitt.sektion i m/s
- Reversibla tryckförändringar i det friktionsfria flödet enligt Bernoullis ekvation
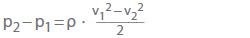
För accelererade flöden, t.ex. minskningar av rördiametern, (p2 – p1) är alltid negativ; För bromsade flöden, t.ex. rörutvidgningar, är den alltid positiv. Vid beräkning av nettotrycksförändringen som den aritmetiska summan av pL och (p2 – p1) måste de irreversibla tryckförlusterna alltid subtraheras.
Influens av högviskösa vätskor på systemets karakteristiska kurva
Då de strömningsdynamiska lagarna behåller sin giltighet för alla newtonska vätskor, är ekvationerna och diagrammen för beräkning av rörfriktionsfaktorer och förlustkoefficienter för ventiler också tillämpliga på viskösa vätskor med en högre viskositet än vatten.
När man beräknar Reynoldstalet Re = v – d / ν måste man helt enkelt ersätta de viskösa vätskornas kinematiska viskositet νz med vattnets viskositet νz.
Detta ger ett lägre Re-tal och, enligt figur 1 Huvudförlust, en större rörfriktionskoefficient λz (Observera: Påverkan från väggens ojämnheter kan nu ofta ignoreras på grund av den större gränsskikttjockleken i flödet).
Alla tryckförluster i rör och ventiler som beräknats för vatten ska extrapoleras med hjälp av förhållandet λz/λw.
Figur 13 Huvudförlust lämpar sig också för allmän praktisk användning: Rörfriktionskoefficienten λz kan snabbt bestämmas som en funktion av flödeshastigheten Q, rörets innerdiameter d och den kinematiska viskositeten νz. Man måste dock komma ihåg att koefficienten λw i detta diagram endast gäller för hydrauliskt släta rör (dvs. inte för grova rör)! Motsvarande λw kan användas för att beräkna förhållandet λz/λw.
Då den statiska komponenten av den systemkarakteristiska kurvan Hsys , se fig. 1 Systemkarakteristisk kurva och fig. 2 Huvud, inte påverkas av viskositeten, kan den dynamiska komponenten av den systemkarakteristiska kurvan för vatten ritas om som en brantare parabel för en viskös fluid.
Influens av icke-newtonska vätskor på systemkarakteristiska kurvan
Då flödeskurvorna inte är raka linjer med konstant linjär viskositet är beräkningen av fallhöjdsförlusterna mycket besvärlig. I detta fall baseras förlustberäkningen på erfarenhet av särskilda vätskor.