Sannolikhet Introduktion: Artiklar och videor med lösningar!

admin 0 Comments Articles

Sannolikhet Introduktion: Artiklar och videor med lösningar!

Tärningskastning, att hitta en parkeringsplats, att vinna i kortspel – detta är bara några situationer där du kanske vill ta reda på oddsen för att en händelse ska inträffa. Om du vill veta hur man hittar sannolikheten måste du först ta reda på vilken typ av fråga du har. Hur du hittar oddsen för att en händelse ska inträffa skiljer sig till exempel från att hitta oddsen för att gruppmedlemmar ska välja samma sak.

Vissa sannolikheter är lätta att identifiera, som att hitta sannolikheten för att kasta tärningar eller välja från en kortlek.

Frågor som involverar binomialsatsen är också lätta att identifiera. I dessa typer av experiment är de enda möjliga utfallen av en händelse ”framgång” eller ”misslyckande”: som ja/nej, huvud/svans eller svart/vit.

Andra frågetyper som du kan stöta på handlar om människor, som:

• Välja en person från en grupp eller kommitté.
• Sannolikheten för att en grupp ska välja samma sak.

Händelser

Vill du ta reda på sannolikheten för att en enkel händelse inträffar? Som att det regnar eller att hitta en parkeringsplats på stan? Se:
Sannolikheten för att en enkel händelse inträffar.
Om du däremot vill ha raka motsatsen, se:
Hur man tar reda på sannolikheten för att en händelse INTE inträffar.

Har din fråga att en händelse inträffar givet en annan händelse? Som sannolikheten att hitta en parkeringsplats, givet att det är matchdag, eller att hitta en viss populär leksak på Black Friday? Om så är fallet, kolla in:

• Odds för en händelse, givet en annan händelse.
• Två händelser som inträffar tillsammans.

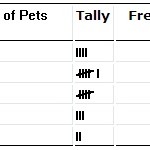
En frekvensfördelningstabell.

Frekvensfördelningar

Har du en frekvensfördelning att arbeta med? Eller kan du göra en frekvensfördelningstabell med dina givna data? Du har till exempel x antal föremål med vissa egenskaper. Sannolikhetsfrekvensfördelning.

Introduktion till sannolikhet: praktiska artiklar och videor.

1. Permutationer och kombinationer: Hur man löser problem
2. Probability Problems:
3. Probability of a and b.
4. Total Probability Rule.
5. Bayes Theorem Problems: Lös dem på ett enkelt sätt: Hur man gör en sannolikhetsfördelning från data.
6. Hur man hittar sannolikheten för att välja en person från en grupp eller kommitté.
7. Hur man hittar sannolikheten för att en händelse INTE inträffar.
8. Probability Frequency Distribution.
9. Hur man hittar sannolikheten för att en enkel händelse inträffar.
10. Random Event: Hur man hittar sannolikheten för att gruppmedlemmar väljer samma sak.
11. Hur man hittar sannolikheten för att två beroende händelser inträffar tillsammans.
12. Hur man hittar sannolikheten för att en händelse inträffar, givet en annan händelse.
13. Hur man använder ett sannolikhetsträd (beslutsträd) för att beräkna odds.
14. Hur man hittar sannolikheten för att dra ett kort från en kortlek.
15. Hur man tar reda på om något är en ömsesidigt uteslutande händelse.
16. Hur man kan se skillnaden mellan beroende och oberoende händelser.
17. Probability: Hur man ritar ett Venn-diagram.
18. Hur man ritar ett Venn-diagram.
19. Hur man skapar ett Euler-diagram.
20. 5 välj 3: hur man löser kombinationer.
21. Hur man använder den grundläggande räkneprincipen.
22. Hur man hittar förväntat värde för en diskret slumpvariabel.

Introduktion till sannolikhet: Definitioner

• Axiomatisk sannolikhet.
• Benfords lag
• Vad är ett binomialförsök?
• Basbelopp och basbeloppsfelet
• Brierpoäng
• Kollektivt uttömmande
• Vad är kombinationer?
• Komplementära händelser.
• Konditionell förväntan
• Vad är villkorlig relativ frekvens?
• Träkningsbar additivitet
• Tomma mängder
• Epistemisk sannolikhet
• Händelserum
• Vad är experimentell sannolikhet?
• Gemensamma sannolikhetsfördelningar
• Begränsande fördelning.
• Maximum Likelihood Estimation
• Memoryless Property.
• Monte Carlo Method.
• Monty Hall Problem
• Vad är en Mutually Exclusive Event?
• Vad är en Mutually Inclusive Events?
• Ömsesidigt oberoende och parvis oberoende.
• Vad är multiplikationsregeln?
• Nash Equilibrium
• Nonempty Set
• Praktikproblem om normal sannolikhet.
• Vad är en normal sannolikhetsdiagram?
• Objektiv sannolikhet
• Vad är oddsförhållandet?
• Prediktiv analys
• Vad är en sannolikhetsfördelningstabell?
• Sannolikhetsmått
• Vad är ett sannolikhetsområde?
• Sannolikhetsvektorer
• Vad är provytor?
• Stokastiska modeller.
• Vad är subjektiv sannolikhet?
• Vad är teoretisk sannolikhet?
• Vad är en urnmodell?

Räknare.

• Online permutationsräknare och kombinationsräknare.

Sannolikhetsformler / Sannolikhetsregler

En av de mest obekväma sakerna som eleverna inte tycker om när det gäller formler är bristen på dem inom sannolikhet och statistik. Det finns ett fåtal grundsatser, bland annat en del notationer som är nödvändiga att känna till:

Sannolikhetsintervall
0 ≤ P(A) ≤ 1
Detta anger att sannolikheten för en händelse ligger någonstans mellan noll och 100 % (i decimaler är det 0 och 1). Du vill komma ihåg den här regeln när du adderar eller multiplicerar sannolikheter för händelser. Om ditt svar är över 100 % är det ett tecken på att du kanske har gjort något fel.

Regel för kompletterande händelser
P(AC) + P(A) = 1
Kompletterande händelser inträffar när det bara finns två utfall, till exempel när man slår ett mynt. Att kasta en tärning för att se om du får en sexa är också komplementärt; de enda två utfallen är att få en sexa (1/6 chans) eller att inte få en sexa (5/6 chans). De två sannolikheterna måste summera till 1.
Du kan också se denna formel skriven så här:
p(A) + p(A’) = 1
som kan omformas algebraiskt till:
p(A’) = 1 – p(A).
Alla tre formler är likvärdiga: vilken terminologi (A’ eller Ac) som används är upp till läroboksförfattaren och läraren. Personligen föredrar jag A’, som jag kallar ”inte A”. Sannolikheten för ”inte A” tycker jag är lättare att förstå än ”komplementet” (antingen inträffar en händelse eller så inträffar den inte).

Additionsregel
P(A∪B) = P(A) + P(B) – P(A∩B)
där ∪ är föreningen och ∩ är skärningspunkten.
Vad detta säger (på engelska!) är att sannolikheten för att händelse A ELLER händelse B inträffar (eller båda samtidigt) är:

• Sannolikheten för att händelse A inträffar på egen hand,
• Plus sannolikheten för att händelse B inträffar på egen hand,
• Plus sannolikheten för att båda händelserna inträffar samtidigt.

Om du har händelser som utesluter varandra kan P(A∩B) inte inträffa (händelserna kan inte inträffa tillsammans), så formeln blir:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Disjunta händelser
Händelserna A och B är disjunkta om:
P(A∩B) = 0
Detta är bara ett annat sätt att säga att händelserna är ömsesidigt uteslutande. De kan inte inträffa samtidigt.

En relaterad formel är P((A∪B)c) eller motsvarande ((A∪B)’). På engelska betyder detta ”not the union”. För att lösa detta räknar du ut föreningen och tar resultatet bort från 1 (eftersom sannolikheten för att händelserna inträffar eller inte inträffar måste summera till 1).

Konditionell sannolikhet
P(A|B) = P(A∩B) / P(B)
Symbolen ”|” betyder ”givet att”. Med andra ord, sannolikheten för att händelse B inträffar, givet att händelse A inträffar. För exempel på hur man använder formeln, se: villkorlig sannolikhet.

Bayes formel
P(A|B) = P(B|A) – P(A) / P(B)
Bayes teorem är ett sätt att räkna ut villkorlig sannolikhet, även om det är något mer nyanserat. I ett nötskal ger den dig den faktiska sannolikheten för en händelse givet information om tester. Till exempel, hur stor är sannolikheten att du har cancer om ditt medicinska test är positivt (svaret = mycket lägre än du tror). För några exempel, se: Bayes teorem Exempel och Posterior Distributions / Posterior Probabilities.

Oberoende händelser
Händelserna A och B är oberoende om en av dem inte påverkar sannolikheten för den andra. Händelser sägs också vara oberoende om följande ekvation gäller:
P(A∩B) = P(A) – P(B).
Denna ekvation härleds från multiplikationsregeln, som säger att P(A∩B) = P(A) * P(B|A). Eftersom vi vet att P(B|A) = P(B) för oberoende händelser kan vi ersätta P(B|A) med P(B), vilket ger oss formeln.

Några anteckningar om sannolikhetsregler

Statistik handlar om slumpen och bollplankning, inte om absoluta tal och det ”rätta svaret”. Titta bara på vilken Gallupundersökning som helst – de är sällan mer än 90 procent säkra på att de har det ”rätta svaret”. Det finns tekniker som du kan använda för att räkna ut odds (som att multiplicera två sannolikheter med varandra eller addera dem). Men förutom kanske binomialfördelningstabellen och formlerna ovan (som i verkligheten inte används så mycket) finns det egentligen inga sannolikhetsformler som du enkelt kan tillämpa. Du måste gå tillbaka till den gamla grundskolehäftklämman, logik (du minns den… den fanns där precis innan de började göra standardiserade tester för att få bort logiken ur dig).

De tre reglerna för sannolikhetsformler:

1. Det finns inga regler (nåja, väldigt få, förutom de som anges ovan).
2. Använd logik, inte ekvationer.
3. Det finns många, många olika sätt att komma fram till svaret – inget av dem använder egentligen formler.

Här är en fråga som kom in i min inkorg i morse och som handlar om sannolikheter:

”Om du försöker samla ihop 6 basebollkort i paket med ostpuffar, om du antar att de är jämnt fördelade, hur många paket med ostpuffar kan du då räkna med att behöva köpa innan du har alla 6 korten?”

Steg 1 för att lösa det här problemet är att inse att du inte kan söka upp svaret i en tabell. För att lösa det måste du tänka som ett barn.

Kort nr 1:Du är 8 år gammal igen och går in i en affär med tillräckligt med pengar för att köpa en påse ostbågar. Du hoppas kunna samla alla 5 basebollkorten men du har inga ännu. Hur stor är chansen att du köper en påse och får ett kort du vill ha?

Svaret är naturligtvis 100 %. Om du köper din första påse har du 100 % chans att det finns ett kort i den som du vill ha.

Kort nr 2: Nu blir det lite knepigare. Du återvänder till butiken för att köpa kort nr 2. Men eftersom du redan har fått kort nr 1, Mickey Mantle. Du vill inte ha honom igen, men det finns en 1/5 chans att du får honom (och därför en 4/5 chans att du inte får honom). Hur många påsar ostbågar måste du köpa för att få kort nr 2 blir ett kvotproblem. Du kan räkna ut det i huvudet, men om du vill modellera det matematiskt måste du ställa upp ekvationen. Om en påse ostbågar ger dig 80 % chans att få det kort du vill ha, hur många påsar måste du köpa för att få 100 % chans?

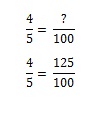
För att få 100 % måste du köpa 1,25 påsar.

Kort nr 3:Oddsen börjar bli svårare. Du har 60 % chans att få det tredje basebollkortet, och du måste köpa 1,667 påsar för att få det tredje kortet.

Kort nr 4:Oddsen börjar bli lite dystra. Du har 40 % chans att få det fjärde basebollkortet, och du måste köpa 2,5 påsar för att få det tredje kortet.

Kort nr 5:Oddsen är emot dig. Du har 20 % chans att få det sista kortet, och du måste köpa 5 påsar för att få det tredje kortet.

Det totala antalet påsar du måste köpa är alltså:
1 + 1,25 + 1,667 + 2,5 + 5
Men vänta! (Och här kommer lite logik in i bilden). Du kan inte gå in i en affär och köpa 1,25 påsar ostbågar, så du måste avrunda uppåt. Ekvationen blir:
1 + 2 + 2 + 2 + 3 + 5 = 13 påsar.

En viktig punkt för formler: kom ihåg att ingenting är absolut. Jag är ganska säker på att om du köper 13 påsar med ostbågar och om du antar att korten är jämnt fördelade, så kommer du att få alla 5 korten. Men … sannolikhet handlar om slumpen, och det kan vara otur för dig att få samma kort tio gånger i rad (jag minns att det hände mig som barn). Men det kan finnas en annan förklaring till din ”otur”, och det är att företagen vill att du ska köpa så många påsar som möjligt, så de försöker få oddsen att fungera till deras fördel. Även om korten är jämnt fördelade kan företaget skicka påsar med korten nr 1, 2 och 3 till en butik (och på så sätt få dig att samla mer än hälften av korten) och nr 4 och 5 till en annan butik.

Vilka andra sätt kan du tänka dig att tillverkarna kan vända oddsen till sin fördel?

Sannolikheten för att en grupp väljer samma sak

Sannolikhetsfrågor kan delas in i olika typer. När du ombeds att ta reda på sannolikheten för att en grupp ska välja samma sak, tar du hänsyn till handlingar av slumpmässiga medlemmar i en grupp (den kan vara så liten som en kommitté eller så stor som befolkningen i USA).
De här sannolikhetsfrågorna ger dig en grupp och ber dig beräkna sannolikheten för att en händelse inträffar för ett visst antal slumpmässiga medlemmar i den gruppen.

Sannolikheten för att en grupp väljer samma sak : steg

Exempel på problem: Det finns 200 personer på en bokmässa. 159 av dem kommer att köpa minst en bok. Om du undersöker 5 slumpmässiga personer som kommer ut genom dörren, hur stor är sannolikheten att de alla kommer att ha köpt minst en bok?

Vad är sannolikheten för att en grupp köper minst en bok?

Steg 1: Omvandla uppgifterna i frågan till en bråkdel. Till exempel kan frasen ”159 personer av 200” omvandlas till: 159/200.

Steg 2: Multiplicera bråket med sig själv. Upprepa för hur många slumpmässiga objekt (dvs. personer) som än väljs. I vårt exempel har vi 5 personer som undersökts, så vi vill ha:

159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
Detta är hur man hittar sannolikheten för att en grupp väljer samma sak!

Tip: Det kan vara lättare att omvandla bråket till en decimal innan du multiplicerar. I det här fallet är 159/200 = 0,795.

Kolla in vår YouTube-kanal för mer hjälp och tips om statistik! Vi har videor för de vanligaste problemen som du sannolikt kommer att stöta på. Plus videor för att använda Excel i statistik > allt från att göra enkla stapeldiagram till att lösa komplexa dataanalysproblem.

——————————————————————————

Behövs hjälp med en läx- eller provfråga? Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert inom området. Dina första 30 minuter med en Chegg-handledare är gratis!