Skewness – Snabb introduktion, exempel och formler
Skewness är ett tal som anger i vilken utsträckning
en variabel är asymmetriskt fördelad.
- Positiv (höger) skevhet exempel
- Negativ (vänster) skevhet exempel
- Populationens skevhet – formel och beräkning
- Samplingens skevhet – formel och beräkning
- Samplingens skevhet – formel och beräkning. Formel och beräkning
- Skewness i SPSS
- Skewness – konsekvenser för dataanalys
Positiv (höger) Skewness Exempel
En forskare har 1,000 personer genomföra några psykologiska tester. För test 5 har testresultaten en skewness = 2,0. Ett histogram av dessa resultat visas nedan.
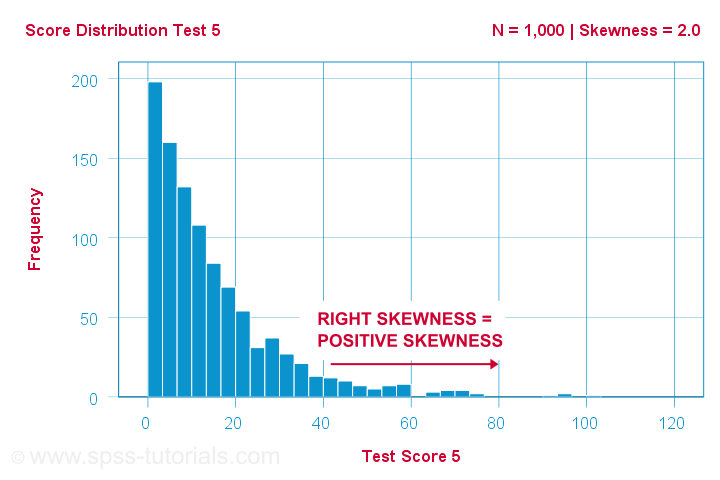
Histogrammet visar en mycket asymmetrisk frekvensfördelning. De flesta får 20 poäng eller lägre men den högra svansen sträcker sig upp till 90 eller så. Denna fördelning är högerskevad.
Om vi rör oss åt höger längs x-axeln går vi från 0 till 20 till 40 poäng och så vidare. Så mot höger i grafen blir poängen mer positiva. Därför är höger skevhet positiv skevhetvilket innebär skevhet > 0. Detta första exempel har skevhet = 2,0 vilket indikeras i det övre högra hörnet av grafen. Poängen är starkt positivt skev.
Negativ (vänster) skevhet Exempel
En annan variabel – poängen på test 2- visar sig ha skevhet = -1,0. Deras histogram visas nedan.

De flesta resultaten ligger mellan 60 och 100 eller så. Den vänstra svansen är dock något utdragen. Så denna fördelning är vänsterskevad.
Högre: till vänster, till vänster. Om vi följer x-axeln till vänster rör vi oss mot mer negativa poäng. Detta är anledningen till att vänster skevhet är negativ skevhet.Och i själva verket är skevhet = -1,0 för dessa poäng. Deras fördelning är vänsterskevad. Den är dock mindre skev – eller mer symmetrisk – än vårt första exempel som hade skewness = 2,0.
Symmetrisk fördelning innebär noll skewness
Slutligt har symmetriska fördelningar skewness = 0. Poängen på test 3 – med skewness = 0,1 – kommer nära.

Nu är observerade fördelningar sällan exakt symmetriska. Detta ses främst för vissa teoretiska provtagningsfördelningar. Några exempel är
- den (vanliga) normalfördelningen;
- t-fördelningen och
- binomialfördelningen om p = 0,5.
Dessa fördelningar är alla exakt symmetriska och har således skewness = 0.000…
Populationens skevhet – formel och beräkning
Om du vill beräkna skevheten för en eller flera variabler är det bara att lämna beräkningarna till någon programvara. Men – för fullständighetens skull – listar jag ändå formlerna.
Om dina data innehåller hela populationen kan du beräkna populationens skewness på följande sätt:
$$$Population\;skewness = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$$$
där
- \(X_i\) är varje enskild poäng;
- \(\mu\) är populationens medelvärde,
- \(\sigma\) är populationens standardavvikelse och
- \(N\) är populationens storlek.
För en exempelberäkning med denna formel, se detta Googlesheet (visas nedan).
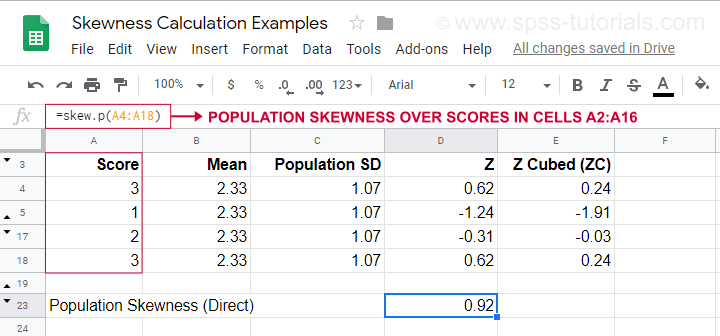
Det visar också hur man får fram populationens skevhet direkt genom att använda=SKEW.P(…)där ”.P” betyder ”population”. Detta bekräftar resultatet av vår manuella beräkning. Tyvärr kan varken SPSS eller JASP beräkna populationens skewness: båda är begränsade till urvalets skewness.
Sampelskjuts – formel och beräkning
Om dina data innehåller ett enkelt slumpmässigt urval från en population använder du
$$$Sample\;skewness = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$$
där
- \(X_i\) är varje enskild poäng;
- \(\overline{X}\) är urvalets medelvärde;
- \(S\) är urvalets standardavvikelse och
- \(N\) är urvalets storlek.
Ett exempel på beräkning visas i detta Googlesheet (visas nedan).
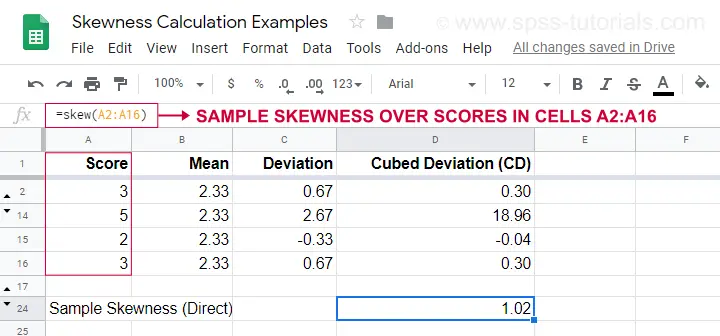
Ett enklare alternativ för att erhålla snedhet i urvalet är att använda=SKEW(…).vilket bekräftar resultatet av vår manuella beräkning.
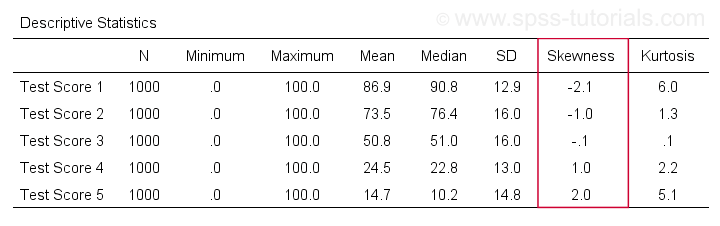
Skewness i SPSS
För det första hänvisar ”skewness” i SPSS alltid till stickprovsskewness: det förutsätter tyst att dina data innehåller ett stickprov snarare än en hel population. Det finns många alternativ för att få fram det. Min favorit är via MEANS eftersom syntaxen och utdata är rena och enkla. Skärmavbilderna nedan guidar dig.

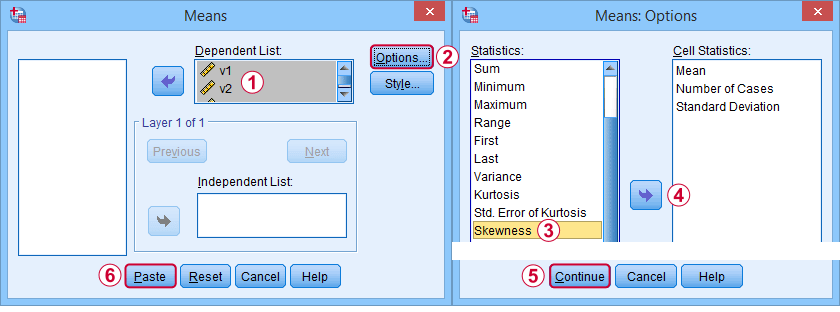
Syntaxen kan vara så enkel sommeans v1 to v5
/cells skew.En mycket komplett tabell – inklusive medelvärden, standardavvikelser, medianer med mera – körs frommeans v1 to v5
/cells count min max mean median stddev skew kurt.Resultatet visas nedan.
Skewness – Implikationer för dataanalys
Många analyser -ANOVA, t-test, regression och andra – kräver normalitetsantagandet: variablerna ska vara normalfördelade i populationen. Normalfördelningen har skewness = 0. Om man observerar en betydande skewness i vissa provdata tyder det på att normalitetsantagandet har brutits.
Sådana överträdelser av normaliteten är inget problem för stora provstorlekar – säg N > 20 eller 25 eller så. I detta fall är de flesta tester robusta mot sådana överträdelser. Detta beror på den centrala gränssatsen. Kort sagt,för stora urvalsstorlekar är skevhet
inget egentligt problem för statistiska tester.Skvhet är dock ofta förknippad med stora standardavvikelser. Dessa kan resultera i stora standardfel och låg statistisk styrka. På samma sätt kan betydande skevhet minska chansen att förkasta någon nollhypotes för att påvisa någon effekt. I detta fall kan ett icke-parametriskt test vara ett klokare val, eftersom det kan ha större effekt.Överträdelser av normaliteten utgör ett verkligt hot
för små urvalsstorlekarav -säg N < 20 eller så. Med små urvalsstorlekar är många tester inte robusta mot ett brott mot normalitetsantagandet. Lösningen – återigen – är att använda ett icke-parametriskt test eftersom dessa inte kräver normalitet.
Sist men inte minst finns det inget statistiskt test för att undersöka om populationens skewness = 0. Ett indirekt sätt att testa detta är ett normalitetstest som
- the Kolmogorov-Smirnov normality test och
- the Shapiro-Wilk normality test.
När normaliteten verkligen behövs – med små urvalsstorlekar – har sådana tester dock låg effekt: de kanske inte uppnår statistisk signifikans även när avvikelserna från normaliteten är allvarliga. På så sätt ger de främst en falsk känsla av säkerhet.




