Syntetisk divisionsmetod
Jag måste säga att syntetisk division är det ”roligaste” sättet att dividera polynom. Den har färre steg för att komma fram till svaret jämfört med metoden för långdivision av polynom. I den här lektionen kommer jag att gå igenom fem (5) exempel som förhoppningsvis ska göra dig bekant med de grundläggande förfarandena för att lyckas dividera polynom med hjälp av syntetisk division.
Saker att komma ihåg:
- Se till att utdelningen är i standardform. Det innebär att potenserna är i fallande ordning.
- Divaren måste vara i formen x – \vänster( c \höger).
Exempel på hur man dividerar polynomier med hjälp av syntetisk division
Exempel 1: Dividera polynomet nedan.
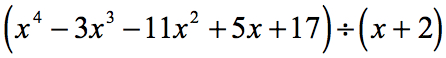
Låt oss granska det givna problemet på nytt och göra de nödvändiga justeringarna, om det behövs.
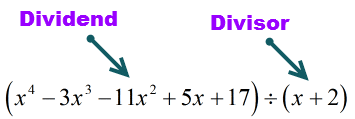
Dividenden (det som ska divideras) är i standardform eftersom exponenterna är i fallande ordning. Det är bra!
Dividenden måste skrivas om som
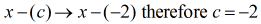
I det här läget kan jag nu ställa in den syntetiska divisionen genom att extrahera koefficienterna i dividenden och sedan rada upp dem ovanpå.
Direkt till vänster placerar du värdet för c = – 2 inne i ”boxen”.
Slutligt konstruerar du en horisontell linje precis under dividendkoefficienterna.
Steg:
1. Släpp den första koefficienten under den horisontella linjen.
2. Multiplicera det tal du släpper med talet i ”rutan”. Oavsett dess produkt placerar du den över den horisontella linjen strax under den andra koefficienten.
3. Addera kolumnen med talen och placera sedan summan direkt under den horisontella linjen.
4. Upprepa processen tills du har slut på kolumner att addera.
Se den animerade lösningen nedan:
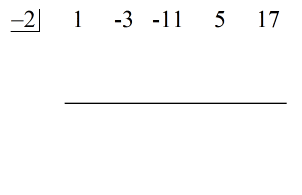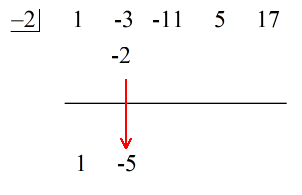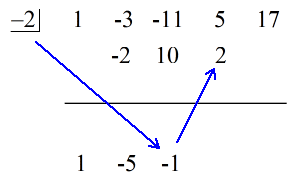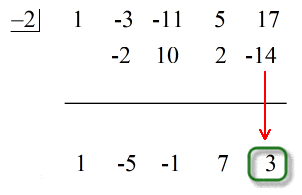
Det sista talet under den horisontella linjen är alltid återstoden! Resten av detta problem är 3.
Hur presenterar vi vårt slutliga svar?
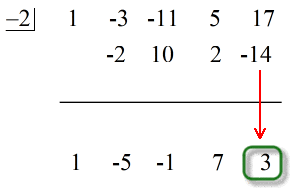
- Visa ditt slutliga svar i formen
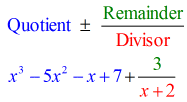
Bemärk att siffrorna under den vågräta linjen utom den sista (resten) är koefficienterna för kvoten.
Mer än så är exponenterna för kvotens variabler alla reducerade med 1.
Exempel 2: Dividera polynomet.
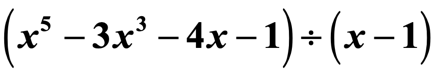
Detta är ingen trickfråga. Lägg märke till att kvoten inte har alla exponenter för variabeln x.
Jag kan se att vi saknar {x^4} och {x^2}. För att inkludera alla koefficienter till variabeln x i fallande potens ska vi skriva om det ursprungliga problemet så här. Fäst nollor på de saknade x-koefficienterna. Uttryck också divisorn som x – (c) vilket tydligt avslöjar värdet på c, det vill säga c = + 1.
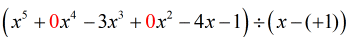
Från den här punkten kan jag nu ställa in siffrorna för att fortsätta med processen.
Steg:
1. Släpp den första koefficienten under den horisontella linjen.
2. Multiplicera det tal du släpper med talet i ”rutan”. Oavsett dess produkt placerar du den över den horisontella linjen strax under den andra koefficienten.
3. Addera kolumnen med siffror och placera sedan summan direkt under den horisontella linjen.
4. Upprepa processen tills du får slut på kolumner att addera.
Se den animerade lösningen nedan:
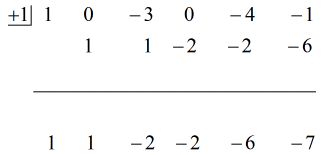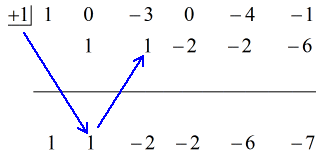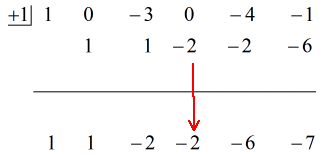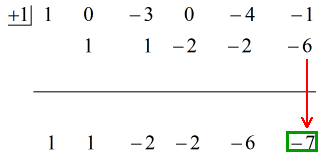
Så genom att sätta det slutliga svaret i formen
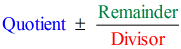
har vi
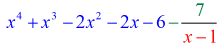
Exempel 3: Dela polynomet nedan.
\left( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Detta börjar bli mer intressant! Kvoten ser definitivt hemsk ut eftersom det saknas en hel del. Inte bara saknar den några x som är {x^3} och {x^2} utan konstanten är också borta.
För att åtgärda detta kommer jag att skriva om det ursprungliga problemet på ett sådant sätt att alla x är medräknade. Men viktigare är att inte glömma att inkludera den saknade konstanten som är noll.
Det ”nya och förbättrade” problemet bör se ut så här:
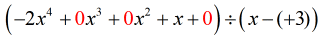
Från här, fortsätt med stegen som vanligt.
Steg:
1. Släpp den första koefficienten under den horisontella linjen.
2. Multiplicera det tal du släpper med talet i ”rutan”. Oavsett dess produkt placerar du den över den horisontella linjen strax under den andra koefficienten.
3. Addera kolumnen med siffror och placera sedan summan direkt under den horisontella linjen.
4. Upprepa processen tills du får slut på kolumner att addera.
Se den animerade lösningen nedan:
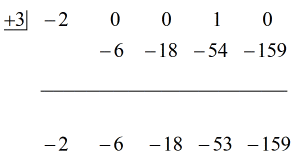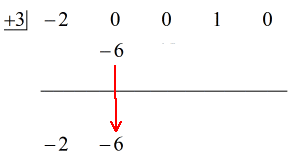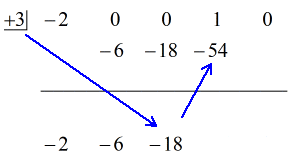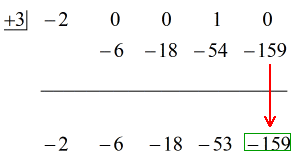
Okej då, det slutgiltiga svaret för detta är
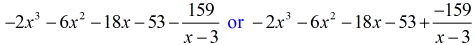
Du kan skriva det slutgiltiga svaret på två sätt. Det första är att använda minus- eller subtraktionssymbolen för att ange att återstoden är negativ. Det andra är att använda +-symbolen men fästa en negativ symbol vid täljaren. De betyder samma sak!
Exempel 4: Dela polynomet nedan.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Låt dig inte avskräckas av detta problem. Det är faktiskt ganska lätt, särskilt nu när du har gått igenom några exempel redan. Kom alltid ihåg att ”fylla i de saknade delarna”, eller hur?
Observera utdelningen och du bör hålla med om att de saknade delarna är {x^4}, {x^3}, {x^2} och x.
Omskriver vi det ursprungliga problemet som är klart för syntetisk division får vi…
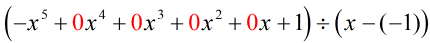
Vi fyllde de saknade x med nollor och löser explicit för c = -1.
Steg:
1. Släpp den första koefficienten under den horisontella linjen.
2. Multiplicera det tal du släpper med talet i ”rutan”. Oavsett dess produkt placerar du den över den horisontella linjen strax under den andra koefficienten.
3. Addera talkolumnen och placera summan direkt under den horisontella linjen.
4. Upprepa processen tills du har slut på kolumner att lägga till.
Se den animerade lösningen nedan:
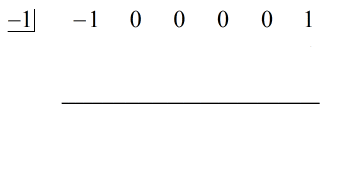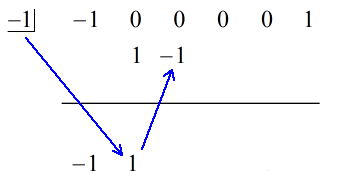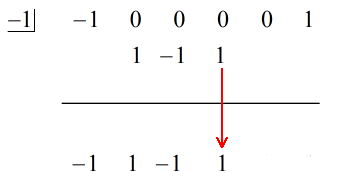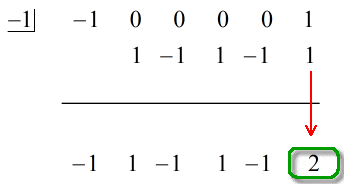
Det sista talet under den horisontella linjen kommer alltid att vara resten. Glöm inte det. I det här fallet är resten lika med 2.
Vårt slutgiltiga svar är
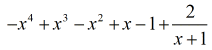
Exempel 5: Dela polynomet med ett binom.
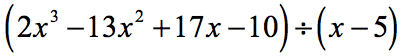
I det här exemplet får vi en rest på noll. När det sker blir divisorn en faktor av utdelningen. Med andra ord delar divisorn jämnt utdelningen.
Genom att undersöka problemet ser jag att det inte saknas några komponenter. Alla potenser av x är redovisade och vi har en konstant. Det är fantastiskt! Detta problem är faktiskt klart för syntetisk division.
Steg:
1. Släpp den första koefficienten under den horisontella linjen.
2. Multiplicera det tal du släpper med talet i ”rutan”. Oavsett dess produkt placerar du den över den horisontella linjen strax under den andra koefficienten.
3. Addera kolumnen med siffror och placera sedan summan direkt under den horisontella linjen.
4. Upprepa processen tills du får slut på kolumner att addera.
Se den animerade lösningen nedan:
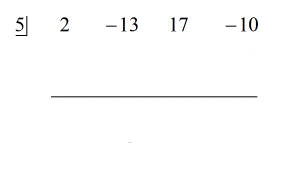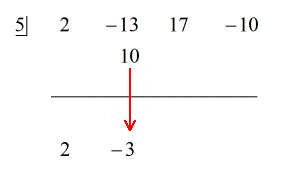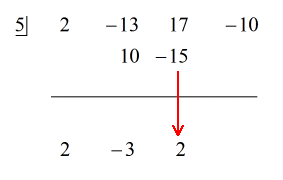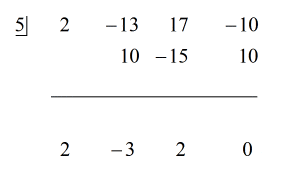
För att återstoden är lika med noll, betyder det att divisorn x – 5 är en faktor av utdelningen
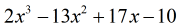
därför
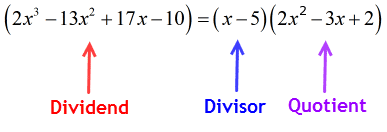
Öva med arbetsblad
Du kanske också är intresserad av:
Addera och subtrahera polynom
Dividuera polynom med hjälp av metoden lång division
Multiplicera binom med hjälp av FOIL-metoden
Multiplicera polynom




