Synthetische delingsmethode
Ik moet zeggen dat synthetische deling de meest “leuke” manier is om veeltermen te delen. Er zijn minder stappen nodig om tot het antwoord te komen dan bij de lange delingsmethode. In deze les zal ik vijf (5) voorbeelden bespreken die je hopelijk vertrouwd zullen maken met de basisprocedures voor het succesvol delen van veeltermen met behulp van synthetische deling.
Dingen om te onthouden:
- Zorg ervoor dat het dividend in de standaardvorm is. Dat betekent dat de machten in afnemende volgorde staan.
- De deler moet de vorm x – links( c rechts) hebben.
Voorbeelden van hoe je veeltermen kunt delen met behulp van de synthetische deling
Voorbeeld 1: Deel de veelterm hieronder.
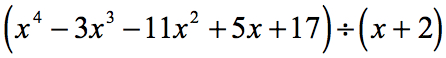
Laten we het gegeven probleem nog eens bekijken en eventueel aanpassen.
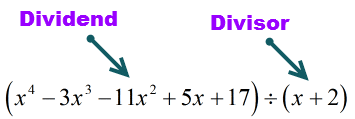
Het dividend (te delen stof) is in standaardvorm omdat de exponenten in aflopende volgorde staan. Dat is goed!
De deler moet herschreven worden als
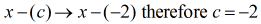
Op dit punt kan ik nu de synthetische deling opstellen door de coëfficiënten van het dividend te extraheren en ze vervolgens op een rij te zetten.
Direct aan de linkerkant plaatst u de waarde van c = – 2 in de “doos”.
Tot slot construeert u een horizontale lijn vlak onder de coëfficiënten van het dividend.
Stappen:
1. Laat de eerste coëfficiënt onder de horizontale lijn vallen.
2. Vermenigvuldig dat getal dat je laat vallen met het getal in het “vakje”. Welk product het ook is, plaats het boven de horizontale lijn net onder de tweede coëfficiënt.
3. Tel de kolom met getallen op en plaats de som direct onder de horizontale lijn.
4. Herhaal dit proces totdat je geen kolommen meer hebt om op te tellen.
Zie de geanimeerde oplossing hieronder:
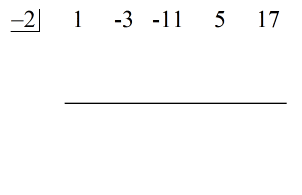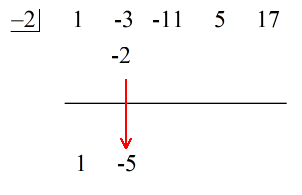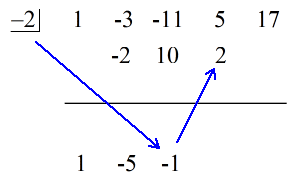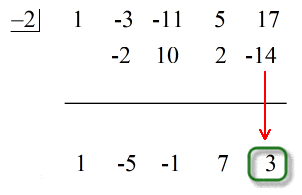
Het laatste getal onder de horizontale lijn is altijd de rest! De rest van dit probleem is 3.
Dus hoe presenteren we ons uiteindelijke antwoord?
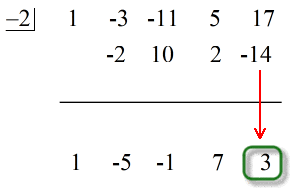
- Toon je uiteindelijke antwoord in de vorm
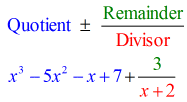
Merk op dat de getallen onder de horizontale lijn behalve het laatste (rest) de coëfficiënten van het quotiënt zijn.
Meer nog, de exponenten van de variabelen van het quotiënt worden allemaal met 1 verminderd.
Voorbeeld 2: Deel de polynoom.
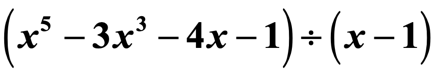
Dit is geen strikvraag. Merk op dat het quotiënt niet alle exponenten van de variabele x bevat.
Ik zie dat we {x^4} en {x^2} missen. Om alle coëfficiënten van variabele x in afnemende macht op te nemen, moeten we het oorspronkelijke probleem als volgt herschrijven. Zet nullen op die ontbrekende x’en. Druk ook de deler uit als x – (c) waardoor de waarde van c duidelijk wordt, namelijk c = + 1.
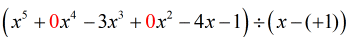
Vanuit dit punt kan ik nu de getallen opstellen om verder te gaan met het proces.
stappen:
1. Laat de eerste coëfficiënt onder de horizontale lijn vallen.
2. Vermenigvuldig dat getal dat u laat vallen met het getal in het “vakje”. Welk product het ook is, plaats het boven de horizontale lijn net onder de tweede coëfficiënt.
3. Tel de kolom met getallen op, plaats dan de som direct onder de horizontale lijn.
4. Herhaal dit proces tot je geen kolommen meer hebt om op te tellen.
Zie de geanimeerde oplossing hieronder:
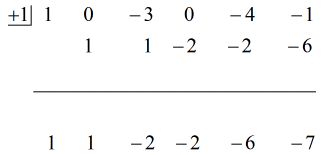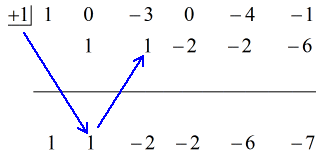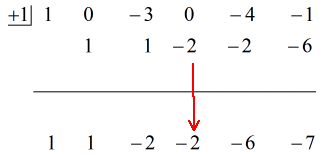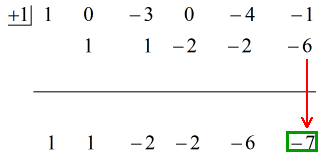
Dus het uiteindelijke antwoord in de vorm
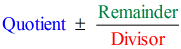
hebben we
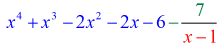
Voorbeeld 3: Deel de onderstaande polynoom.
Links( { – 2{x^4} + x} \rechts) \div \left( {x – 3} \rechts)
Dit wordt interessanter! Het quotient ziet er verschrikkelijk uit omdat het veel mist. Niet alleen ontbreken enkele x-en, namelijk {x^3} en {x^2}, maar ook de constante is weg.
Om dit op te lossen, zal ik het oorspronkelijke probleem zo herschrijven dat alle x-en aan bod komen. Maar wat belangrijker is, vergeet niet de ontbrekende constante, die nul is, mee te rekenen.
Het “nieuwe en verbeterde” probleem moet er als volgt uitzien:
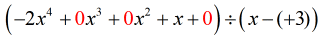
Van hieruit gaat u verder met de stappen zoals u gewend bent.
Stappen:
1. Laat de eerste coëfficiënt onder de horizontale lijn vallen.
2. Vermenigvuldig dat getal dat u laat vallen met het getal in het “vakje”. Welk product het ook is, plaats het boven de horizontale lijn net onder de tweede coëfficiënt.
3. Tel de kolom met getallen op, plaats dan de som direct onder de horizontale lijn.
4. Herhaal dit proces tot je geen kolommen meer hebt om op te tellen.
Zie de geanimeerde oplossing hieronder:
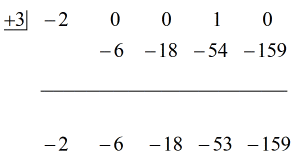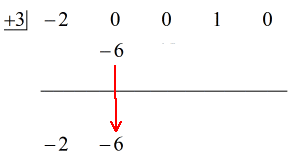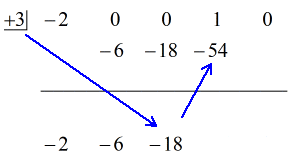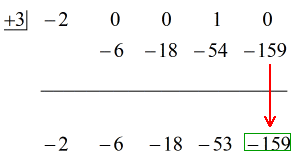
Okee dan, het uiteindelijke antwoord voor dit is
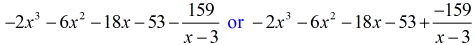
Je kunt het uiteindelijke antwoord op twee manieren schrijven. De eerste manier is door het min- of aftreksymbool te gebruiken om aan te geven dat de rest negatief is. De tweede manier is door het +-teken te gebruiken, maar een negatief teken aan de teller te koppelen. Ze betekenen hetzelfde!
Voorbeeld 4: Deel de onderstaande polynoom.
Links( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Gedraag je niet ontmoedigd door dit probleem. Dit is eigenlijk heel gemakkelijk, vooral nu je al een paar voorbeelden hebt doorgenomen. Denk er altijd aan om “de ontbrekende delen in te vullen”, goed?
Bekijk het dividend en je zou het met me eens moeten zijn dat de ontbrekende delen {x^4}, {x^3}, {x^2}, en x zijn.
Herschrijven we het oorspronkelijke probleem dat synthetisch deelbaar is, dan krijgen we…
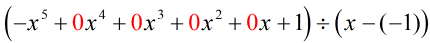
We vullen de ontbrekende x’en aan met nullen en lossen expliciet op voor c = -1.
Stappen:
1. Laat de eerste coëfficiënt onder de horizontale lijn vallen.
2. Vermenigvuldig dat getal dat je laat vallen met het getal in het “vakje”. Welk product het ook is, plaats het boven de horizontale lijn juist onder de tweede coëfficiënt.
3. Tel de kolom van getallen op, plaats dan de som juist onder de horizontale lijn.
4. Herhaal dit proces totdat je geen kolommen meer hebt om op te tellen.
Zie de geanimeerde oplossing hieronder:
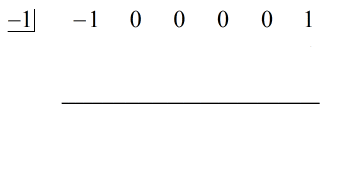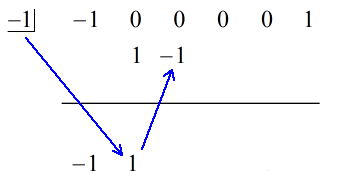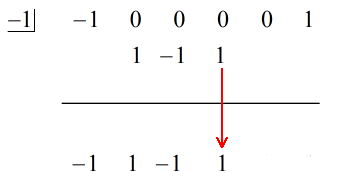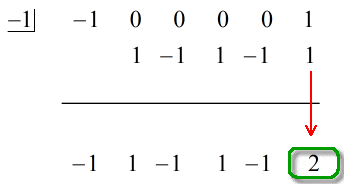
Het laatste getal onder de horizontale lijn zal altijd de rest zijn. Vergeet dat niet. In dit geval is de rest gelijk aan 2.
Ons uiteindelijke antwoord is
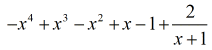
Voorbeeld 5: Deel de polynoom door een binomiaal.
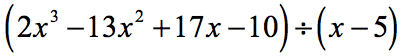
In dit voorbeeld zullen we een rest van nul krijgen. Als dat gebeurt, wordt de deler een factor van het dividendsaldo. Met andere woorden, de deler deelt de deling evenredig.
Als ik het probleem bekijk, zie ik dat er geen ontbrekende componenten zijn. Alle machten van x’en zijn geteld, en we hebben een constante. Dat is mooi! Dit probleem is in feite synthetische-deling-klaar.
Stappen:
1. Laat de eerste coëfficiënt onder de horizontale lijn vallen.
2. Vermenigvuldig dat getal dat je laat vallen met het getal in het “vakje”. Welk product het ook is, plaats het boven de horizontale lijn net onder de tweede coëfficiënt.
3. Tel de kolom met getallen op, plaats dan de som direct onder de horizontale lijn.
4. Herhaal dit proces tot je geen kolommen meer hebt om op te tellen.
Zie de geanimeerde oplossing hieronder:
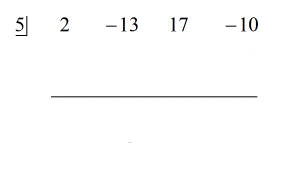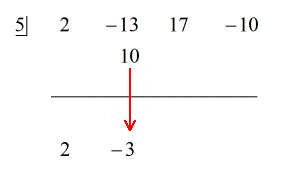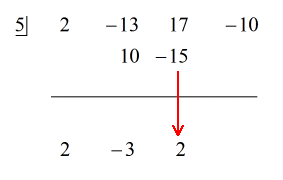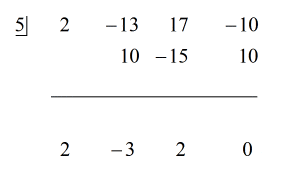
Omdat de rest gelijk is aan nul, betekent dit dat de deler x – 5 een factor is van het dividend
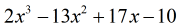
daarom
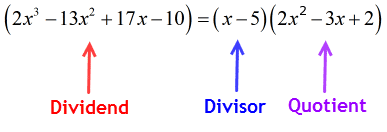
Practice with Worksheets
Je bent misschien ook geïnteresseerd in:
Tellen en aftrekken van veeltermen
Delen van veeltermen met behulp van de lange delingsmethode
Vermenigvuldigen van binomialen met behulp van de FOIL-methode
Vermenigvuldigen van veeltermen




