Twee manieren om breuken te delen en enkele voorbeelden
In dit bericht gaan we leren hoe we breuken kunnen delen. Om dit te doen, gaan we kijken naar twee verschillende methoden:
Methode 1 voor het delen van breuken: Kruislings vermenigvuldigen
- Deze methode bestaat uit het vermenigvuldigen van de teller van de eerste breuk met de noemer van de tweede breuk en vervolgens schrijven we het antwoord in de teller van de resulterende breuk.
- Volgende vermenigvuldigen we de noemer van de eerste breuk met de teller van de tweede breuk en vervolgens schrijven we het antwoord in de noemer van de resulterende breuk*.
- Tot slot vereenvoudigen we de uiteindelijke breuk.
Om bijvoorbeeld de breuk
![]()
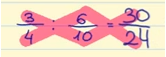
te delen, vermenigvuldigen we de teller van de eerste breuk (3) met de noemer van de tweede breuk (10). Dit geeft ons de teller voor de laatste breuk: 3 x 10 = 30.
Volgende, we vermenigvuldigen de noemer van de eerste breuk (4) met de teller van de tweede breuk (6). Dit geeft ons de noemer van de uiteindelijke breuk: 4 x 6 = 24.
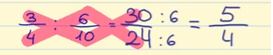
De laatste stap is het vereenvoudigen van de breuk. Aangezien beide getallen veelvouden van 6 zijn, kunnen we de teller en de noemer door 6 delen.
30 ÷ 6 = 5
24 ÷ 6 = 4
Het resultaat van de deling is dus 5/4.
Methode 2 om breuken te delen: Omkeren en vermenigvuldigen
- Stap 1: Keer de tweede breuk om. Dat wil zeggen, verwissel de teller met de noemer.
- Stap 2: Vereenvoudig elke teller met elke noemer.
- Stap 3: Vermenigvuldig over.
Voorbeeld, we gaan delen:

Stap 1: We keren de tweede breuk 6/4 om. Dit wordt 4/6.
Stap 2: We vereenvoudigen de tellers met de noemers.
Numerators zijn:
12 = 2 x 2 x 3
4 = 2 × 2
Denominators zijn:
5 = 5
6 = 2 × 3
We kunnen zowel van teller als van noemer een 2 en een 3 vereenvoudigen. We noemen dit proces “cross canceling” als de ene teller een gemeenschappelijke factor heeft met de andere noemer.
En we vermenigvuldigen over:
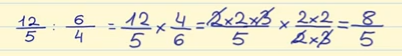
We hopen dat je dit bericht leuk vond.
Als je meer voorbeelden wilt zien, bezoek dan onze vorige post over woordproblemen met deling van breuken en Hoe breuken te vereenvoudigen: Laagste Termen Breuken.
Als je nog veel meer wiskunde wilt leren, meld je dan aan op Smartick.
Leer meer:
- Leer en oefen hoe je breuken kunt aftrekken of optellen
- Leer en oefen hoe je breuken kunt vermenigvuldigen
- Leer hoe je breuken kunt delen met twee verschillende methodes
- Leer hoe je breuken kunt aftrekken Breuken
- Oefenen met optellen van breuken met voorbeelden



- Auteur
- Recent Posts
Een multidisciplinair en multicultureel team bestaande uit wiskundigen, leraren, professoren en andere onderwijsprofessionals!
Zij streven ernaar de best mogelijke wiskundige inhoud te creëren.
- Voorbeelden van 3e graad wiskunde woordproblemen met oplossingen – 03/25/2021
- Opeenvolgende binnenhoeken: Wat ze zijn en hoe ze te vinden met voorbeelden – 03/11/2021
- Voorbeelden van tweede graad wiskundeproblemen met oplossingen – 02/04/2021




