Área de la superficie de un cilindro – Explicación y ejemplos
Antes de entrar en el tema del área de la superficie de un cilindro, vamos a repasar un cilindro. En geometría, un cilindro es una figura tridimensional con dos bases circulares paralelas entre sí y una superficie curva.
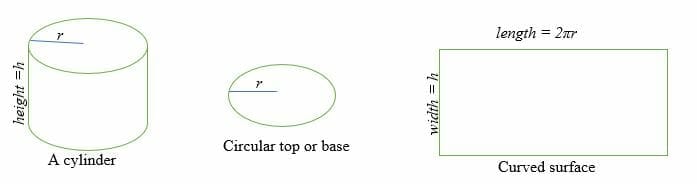
¿Cómo encontrar el área de la superficie de un cilindro?
El área de la superficie de un cilindro es la suma de dos caras circulares paralelas y congruentes y el área de la superficie curva.
Este artículo tratará sobre cómo encontrar el área de la superficie total y el área de la superficie lateral de un cilindro.
Para calcular el área de la superficie de un cilindro, es necesario encontrar el área de la base (B) y el área de la superficie curva (CSA). Por lo tanto, el área superficial o la superficie total de un cilindro es igual a la suma del área de la base por dos y el área de la superficie curva.
La superficie curva de un cilindro es igual a un rectángulo cuya longitud es 2πr y cuya anchura es h.
Donde r = radio de la cara circular y h = altura del cilindro.
El área de la superficie curva = Área de un rectángulo =l x w = πdh
El área de la base, B = Área de un círculo = πr2
La fórmula del área de un cilindro
La fórmula de la superficie total de un cilindro viene dada por:
Superficie total de un cilindro = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Donde 2πr2 es el área de las caras circulares superior e inferior, y 2πrh es el área de la superficie curva.
Tomando 2πr como factor común del lado derecho, obtenemos;
TSA = 2πr (h + r) ……………………………………. (Fórmula del área superficial de un cilindro)
Resolvamos problemas de ejemplo que impliquen el área superficial de un cilindro.
Ejemplo 1
Hallar la superficie total de un cilindro cuyo radio es de 5 cm y su altura es de 7 cm.
Solución
Por la fórmula,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Ejemplo 2
Hallar el radio de un cilindro cuya superficie total es de 2136,56 pies cuadrados, y la altura es de 3 pies.
Solución
Dado:
TSA = 2136.56 pies cuadrados
Altura, h = 3 pies
Pero, TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
Por la propiedad distributiva de la multiplicación en el lado derecho, tenemos,
2136,56 = 18,84r + 6,28r2
Dividir cada término por 6,28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (una ecuación cuadrática)
Resolviendo la ecuación mediante la fórmula cuadrática, obtenemos,
r = 17
Por tanto, el radio del cilindro es de 17 pies.
Ejemplo 3
El coste de pintar un contenedor cilíndrico es de 0,04 dólares por cm2. Encuentre el coste de pintar 20 contenedores de radio, 50 cm, y altura, 80 cm.
Solución
Calcule la superficie total de 20 contenedores.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
La superficie total de 20 contenedores = 40.820 cm2 x 20
=816.400 cm2
El coste de la pintura = 816.400 cm2 x $0.04 por cm2
= 32.656 dólares.
Por lo tanto, el coste de pintar 20 contenedores es de 32.656 dólares.
Ejemplo 4
Hallar la altura de un cilindro si su superficie total es de 2552 in2 y el radio es de 14 in.
Solución
Dado:
TSA = 2552 pul2
Radio, r = 14 pulg.
Pero, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Divide ambos lados por 87,92 para obtener,
29.026 = 14 + h
Reste por 14 en ambos lados.
h = 15
Por lo tanto, la altura del cilindro es de 15 pulg.
Superficie lateral de un cilindro
Como se ha dicho antes, el área de la superficie curva de un cilindro es lo que se denomina superficie lateral. En palabras sencillas, el área de la superficie lateral de un cilindro es el área de un cilindro, excluyendo el área de la base y el fondo (superficie circular).
La fórmula da el área de la superficie lateral de un cilindro;
LSA = 2πrh
Ejemplo 5
Hallar el área de la superficie posterior de un cilindro cuyo diámetro es de 56 cm y su altura es de 20 cm.
Solución
Dado:
Diámetro = 56 cm, por tanto radio, r =56/2 = 28 cm
Altura, h = 20 cm
Por, la fórmula,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Por tanto, la superficie lateral del cilindro es de 3516,8 cm2.
Ejemplo 6
La superficie lateral de un cilindro es de 144 pies2. Si el radio del cilindro es de 7 pies, hallar la altura del cilindro.
Solución
Dado;
LSA = 144 pies2
Radio, r = 7 pies




