Introducción a la probabilidad: ¡Artículos y vídeos con soluciones!
 Lanzamiento de dados, encontrar una plaza de aparcamiento, ganar a las cartas; Estas son sólo algunas situaciones en las que podrías querer encontrar las probabilidades de que ocurra un evento. Si quieres saber cómo encontrar la probabilidad, primero tienes que averiguar qué tipo de pregunta tienes. Por ejemplo, la forma de encontrar las probabilidades de que ocurra un evento es diferente de encontrar las probabilidades de que los miembros de un grupo elijan la misma cosa.
Lanzamiento de dados, encontrar una plaza de aparcamiento, ganar a las cartas; Estas son sólo algunas situaciones en las que podrías querer encontrar las probabilidades de que ocurra un evento. Si quieres saber cómo encontrar la probabilidad, primero tienes que averiguar qué tipo de pregunta tienes. Por ejemplo, la forma de encontrar las probabilidades de que ocurra un evento es diferente de encontrar las probabilidades de que los miembros de un grupo elijan la misma cosa.
Algunas probabilidades son fáciles de identificar, como encontrar las probabilidades de tirar los dados o de elegir de una baraja de cartas.
Las preguntas que implican el teorema del binomio también son fáciles de identificar. En este tipo de experimentos, los únicos resultados posibles de un evento son «Éxito» o «Fracaso»: como sí/no, cara/cara o blanco/negro.
Otros tipos de preguntas que puede encontrar tienen que ver con las personas, como:
- Seleccionar a una persona de un grupo o comité.
- Probabilidad de que un grupo elija lo mismo.
Eventos
¿Quiere encontrar la probabilidad de que ocurra un simple evento? Como que llueva, o que encuentres una plaza de aparcamiento en el centro? Consulte:
Probabilidad de que ocurra un suceso simple.
Por otro lado, si quiere exactamente lo contrario, consulte:
Cómo averiguar la probabilidad de que un suceso NO ocurra.
¿Su pregunta se refiere a que un suceso ocurra dado otro suceso? Como las probabilidades de encontrar una plaza de aparcamiento, dado que es día de partido, o de encontrar un determinado juguete popular en el Black Friday? Si es así, comprueba:
- Probabilidades de un evento, dado otro evento.
- Dos eventos que ocurren juntos.
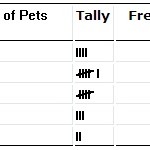
Una tabla de distribución de frecuencias.
Distribuciones de frecuencias
¿Tienes una distribución de frecuencias para trabajar? ¿O eres capaz de hacer una tabla de distribución de frecuencias con tus datos dados? Por ejemplo, tienes x número de elementos con un determinado rasgo. Distribución de frecuencias de la probabilidad.
Introducción a la probabilidad: artículos y vídeos sobre cómo hacerlo.
- Permutaciones y combinaciones: Cómo resolver problemas
- Problemas de probabilidad: Resuélvelos de forma fácil!
- Probabilidad de a y b.
- Regla de la probabilidad total.
- Problemas del Teorema de Bayes: Pasos de fácil solución.
- Probabilidad previa (incluyendo la no informativa y la conjugada).
- Cómo hacer una distribución de probabilidad a partir de datos.
- Cómo hallar la probabilidad de seleccionar a una persona de un grupo o comité.
- Cómo encontrar la Probabilidad de que un Evento NO Suceda.
- Distribución de la Frecuencia de la Probabilidad.
- Cómo Encontrar la Probabilidad de que un Evento Simple Suceda.
- Evento Aleatorio: Probabilidad dado un porcentaje.
- Cómo hallar la probabilidad de que los miembros de un grupo elijan la misma cosa.
- Cómo hallar la probabilidad de que dos sucesos dependientes ocurran juntos.
- Cómo hallar la probabilidad de que ocurra un suceso, dado otro suceso.
- Cómo utilizar un árbol de probabilidad (árbol de decisión) para calcular las probabilidades.
- Cómo encontrar la probabilidad de sacar una carta de una baraja.
- Cómo averiguar si algo es un suceso mutuamente excluyente.
- Cómo diferenciar entre sucesos dependientes e independientes.
- Probabilidad: Lanzamiento de dados.
- Cómo dibujar un diagrama de Venn.
- Cómo crear un diagrama de Euler.
- 5 elija 3: cómo resolver combinaciones.
- Cómo utilizar el principio fundamental de recuento.
- Cómo encontrar el valor esperado para una variable aleatoria discreta.
Introducción a la probabilidad: Definiciones
- Probabilidad axiomática.
- Ley de Benford
- ¿Qué es un experimento binomial?
- Tasa base y falacia de la tasa base
- Puntuación de Brier
- Colectivamente exhaustiva
- ¿Qué son las combinaciones?
- Eventos complementarios.
- Expectativa condicional
- ¿Qué es la frecuencia relativa condicional?
- Aditividad Contable
- Conjunto Vacío
- Probabilidad Epistémica
- Espacios de sucesos.
- ¿Qué es la Probabilidad Experimental?
- Distribuciones de Probabilidad Conjuntas.
- Distribución Limitante.
- Estimación de máxima verosimilitud
- Propiedad de ausencia de memoria.
- Método Monte Carlo.
- Problema de Monty Hall
- ¿Qué es un suceso mutuamente excluyente?
- ¿Qué es un suceso mutuamente incluyente?
- Sucesos mutuamente independientes y sucesos mutuamente independientes.
- ¿Qué es la regla de la multiplicación?
- Equilibrio de Nash
- Conjunto no vacío
- Problemas de práctica de probabilidad normal.
- ¿Qué es un gráfico de probabilidad normal?
- Probabilidad objetiva
- ¿Qué es la razón de probabilidades?
- Análisis predictivo
- ¿Qué es una tabla de distribución de probabilidad?
- Medida de probabilidad
- ¿Qué es un espacio de probabilidad?
- Vectores de probabilidad
- ¿Qué son los espacios muestrales?
- Modelos estocásticos.
- ¿Qué es la probabilidad subjetiva?
- ¿Qué es la probabilidad teórica?
- ¿Qué es un modelo de urna?
Calculadoras.
- Calculadora de permutaciones y combinaciones online.
Fórmulas de probabilidad / Reglas de probabilidad
Una de las cosas más incómodas que no les gusta a los estudiantes es la falta de fórmulas en probabilidad y estadística. Hay unos cuantos elementos básicos, entre los que se incluyen algunas notaciones que hay que conocer:
Rango de probabilidad
0 ≤ P(A) ≤ 1
Esto establece que la probabilidad de un suceso está en algún lugar entre el cero y el 100% (como decimal, eso es 0 y 1). Deberás recordar esta regla cuando sumes o multipliques las probabilidades de los sucesos. Si tu respuesta es superior al 100%, es una pista de que podrías haber hecho algo mal.
Regla de los sucesos complementarios
P(AC) + P(A) = 1
Los sucesos complementarios ocurren cuando sólo hay dos resultados, como lanzar una moneda. Lanzar un dado para ver si se obtiene un seis también es complementario; los dos únicos resultados son obtener un seis (una probabilidad de 1/6) o no obtener un seis (una probabilidad de 5/6). Las dos probabilidades deben sumar 1.
También puede ver esta fórmula escrita así:
p(A) + p(A’) = 1
que puede reordenarse algebraicamente para que diga:
p(A’) = 1 – p(A).
Las tres fórmulas son equivalentes: la terminología que se utilice (A’ o Ac) depende del autor del libro de texto y del profesor. Personalmente, prefiero A’, que llamo «no A». La probabilidad de «no A», creo, es más fácil de comprender que la del «complemento» (o sucede un suceso, o no sucede).
Regla de adición
P(A∪B) = P(A) + P(B) – P(A∩B)
donde ∪ es la unión y ∩ es la intersección.
Lo que esto está diciendo (¡en inglés!) es que la probabilidad de que ocurra el evento A O el evento B (o ambos al mismo tiempo) es:
- La probabilidad de que ocurra el evento A por sí solo,
- Más la probabilidad de que ocurra el evento B por sí solo,
- Más la probabilidad de que ocurran ambos eventos al mismo tiempo.
Si tienes eventos mutuamente excluyentes, entonces P(A∩B) no puede ocurrir (los eventos no pueden ocurrir juntos), por lo que la fórmula se convierte en:
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)
Eventos disjuntos
Los eventos A y B son disjuntos si:
P(A∩B) = 0
Esta es sólo otra forma de decir que los eventos son mutuamente excluyentes. No pueden ocurrir al mismo tiempo.
Una fórmula relacionada es P((A∪B)c) o, equivalentemente ((A∪B)’). En inglés, esto dice «not the union». Para resolverlo, hay que calcular la unión y restar el resultado a 1 (porque la probabilidad de que los sucesos ocurran o no deben sumar 1).
Probabilidad condicional
P(A|B) = P(A∩B) / P(B)
El símbolo «|» significa «dado que». En otras palabras, la probabilidad de que ocurra el suceso B, dado que ocurre el suceso A. Para ver ejemplos de cómo utilizar la fórmula, véase: probabilidad condicional.
Fórmula de Bayes
P(A|B) = P(B|A) – P(A) / P(B)
El teorema de Bayes es una forma de calcular la probabilidad condicional, aunque es algo más matizada. En pocas palabras, te da la probabilidad real de un suceso dada la información sobre las pruebas. Por ejemplo, cuál es la probabilidad de que tengas cáncer si tu prueba médica es positiva (respuesta = mucho menos de lo que crees). Para ver algunos ejemplos, consulte: Ejemplos del Teorema de Bayes y Distribuciones Posteriores / Probabilidades Posteriores.
Eventos independientes
Los eventos A y B son independientes si uno de ellos no afecta a la probabilidad del otro. También se dice que los sucesos son independientes si se cumple la siguiente ecuación.
P(A∩B) = P(A) – P(B).
Esta ecuación se deriva de la regla de la multiplicación, que dice que P(A∩B) = P(A) * P(B|A). Como sabemos que P(B|A) = P(B) para sucesos independientes, podemos sustituir P(B|A) por P(B), lo que nos da la fórmula.
Algunos apuntes sobre las reglas de la probabilidad
La estadística se basa en el azar y los cálculos, no en los absolutos ni en la «respuesta correcta». Basta con buscar cualquier encuesta de Gallup: rara vez tienen más del 90% de confianza en que tienen la «respuesta correcta». Hay técnicas que se pueden utilizar para calcular las probabilidades (como multiplicar dos probabilidades o sumarlas). Sin embargo, aparte de la tabla de distribución binomial y las fórmulas anteriores (que en la vida real no se utilizan mucho), no hay ninguna fórmula de probabilidad que se pueda aplicar fácilmente. Tienes que volver a ese viejo elemento básico de la escuela primaria, la lógica (la recuerdas… estaba ahí justo antes de que empezaran a hacer pruebas estandarizadas para sacarte la lógica).
Las tres reglas de las fórmulas de probabilidad:
- No hay reglas (bueno, muy pocas, excepto las enumeradas arriba).
- Usa la lógica, no las ecuaciones.
- Hay muchas, muchas maneras diferentes de llegar a la respuesta – ninguna de las cuales usa realmente fórmulas.
Aquí hay una pregunta que llegó a mi bandeja de entrada esta mañana que aborda las probabilidades:
«Si tratas de coleccionar 6 tarjetas de béisbol que vienen en paquetes de bocadillos de queso, suponiendo que se distribuyen uniformemente ¿cuántos paquetes de bocadillos de queso esperarías comprar antes de tener las 6 tarjetas?»
El paso 1 para resolver este problema es darse cuenta de que no puedes buscar la respuesta en una tabla. Para resolverlo, tienes que pensar como un niño.
Carta# 1:Vuelves a tener 8 años y entras en una tienda con suficiente dinero para comprar una bolsa de bocadillos de queso. Esperas coleccionar las 5 tarjetas de béisbol, pero aún no tienes ninguna. ¿Cuáles son las probabilidades de que compres una bolsa y consigas una tarjeta que quieras?
La respuesta, por supuesto, es 100%. Compra tu primera bolsa, y tienes el 100% de probabilidades de que haya una carta en ella que quieras.
Carta # 2: Ahora se pone un poco más complicado. Vuelves a la tienda para conseguir la tarjeta#2. Pero como ya tienes la tarjeta #1, Mickey Mantle. No lo quieres de nuevo, pero hay una probabilidad de 1/5 de que lo consigas (y por tanto una probabilidad de 4/5 de que no lo consigas). Cuántas bolsas de queso tendrás que comprar para conseguir la carta nº 2 se convierte en un problema de proporción. Podrías calcularlo en tu cabeza, pero si quieres modelarlo matemáticamente tienes que establecer la ecuación. Si una bolsa de bocadillos de queso te da un 80% de posibilidades de conseguir la carta que quieres, ¿cuántas bolsas tienes que comprar para conseguir un 100% de posibilidades?
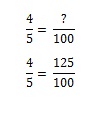
Para conseguir el 100% tendrías que comprar 1,25 bolsas.
Carta#3:Las probabilidades empiezan a ser más difíciles. Tienes un 60% de posibilidades de conseguir la tercera carta de béisbol, y tendrás que comprar 1,667 bolsas para conseguir esa tercera carta.
Carta# 4:Las probabilidades empiezan a ser un poco más desalentadoras. Tienes un 40% de posibilidades de conseguir la cuarta carta de béisbol, y tendrás que comprar 2,5 bolsas para conseguir esa tercera carta.
Carta# 5:Las probabilidades están en tu contra. Tienes un 20% de posibilidades de conseguir la última carta, y tendrás que comprar 5 bolsas para conseguir esa tercera carta.
Así que la cantidad total de bolsas que tendrás que comprar es igual a:
1 + 1,25 + 1,667 + 2,5 + 5
¡Pero espera! (Y aquí es donde entra un poco de lógica). No puedes ir a una tienda y comprar 1,25 bolsas de bocadillos de queso, así que tendrás que redondear. La ecuación se convierte en:
1 + 2 + 2 + 3 + 5 = 13 bolsas.
Un punto importante para las fórmulas: recuerda que nada es absoluto. Estoy razonablemente seguro de que si usted comprara 13 bolsas de bocadillos de queso y asumiendo que las cartas están distribuidas uniformemente, que usted obtendría las 5 cartas. Pero… la probabilidad tiene que ver con el azar, y podría ser sólo tu mala suerte que te tocara la misma carta 10 veces seguidas (recuerdo que eso me pasaba a mí cuando era niño). Pero podría haber otra explicación para tu «mala suerte», y es que las empresas quieren que compres tantas bolsas como sea posible, así que intentarán que las probabilidades jueguen a su favor. Incluso si las cartas se distribuyen uniformemente, la empresa podría enviar bolsas con las cartas nº 1, nº 2 y nº 3 a una tienda (con lo que te atraería consiguiendo que recogieras más de la mitad de las cartas) y las nº 4 y nº 5 a otra tienda.
¿Qué otras formas se le ocurren para que los fabricantes puedan poner las probabilidades a su favor?
Probabilidad de que un grupo elija lo mismo
Las preguntas de probabilidad se pueden dividir en diferentes tipos. Cuando te piden que encuentres la probabilidad de que un grupo elija lo mismo, estás considerando las acciones de miembros aleatorios de un grupo (puede ser tan pequeño como un comité o puede ser tan grande como la población de los Estados Unidos).
Estas preguntas de probabilidad le dan un grupo, y le piden que calcule la probabilidad de que ocurra un evento para un cierto número de miembros al azar dentro de ese grupo.
Probabilidad de que un grupo elija lo mismo : Pasos
Problema de muestra: Hay 200 personas en una feria de libros. 159 de ellas comprarán al menos un libro. Si se encuesta a 5 personas al azar que salen por la puerta, ¿cuál es la probabilidad de que todas ellas hayan comprado al menos un libro?

¿Cuál es la probabilidad de que un grupo compre al menos un libro?
Paso 1: Convierte los datos de la pregunta en una fracción. Por ejemplo, la frase «159 personas de 200» se puede convertir en: 159/200.
Paso 2: Multiplicar la fracción por sí misma. Repita la operación para el número de elementos aleatorios (es decir, personas) que se elijan. En nuestro ejemplo, tenemos 5 personas encuestadas, por lo que queremos:
159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0,3176
¡Así se halla la probabilidad de que un grupo elija lo mismo!
Consejo: Puede ser más fácil convertir la fracción en un decimal antes de multiplicar. En este caso, 159/200 = 0,795.
¡Consulta nuestro canal de YouTube para obtener más ayuda y consejos sobre estadísticas! Tenemos vídeos para los problemas más comunes con los que te puedes encontrar. Además de vídeos para utilizar Excel en estadística > todo, desde la elaboración de gráficos de barras básicos hasta la resolución de complejos problemas de análisis de datos.
Stephanie Glen. «Introducción a la probabilidad: Artículos y vídeos con soluciones». De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/probability-and-statistics/probability-main-index/
——————————————————————————
¿Necesitas ayuda con una tarea o pregunta de examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!




