Método de división sintética
Debo decir que la división sintética es la forma más «divertida» de dividir polinomios. Tiene menos pasos para llegar a la respuesta en comparación con el método de división larga de polinomios. En esta lección, repasaré cinco (5) ejemplos que deberían familiarizarte con los procedimientos básicos para dividir polinomios con éxito utilizando la división sintética.
Cosas a recordar:
- Asegúrate de que el dividendo está en forma estándar. Eso quiere decir que las potencias están en orden decreciente.
- El divisor debe estar en la forma x – \left( c \right).
Ejemplos de cómo dividir polinomios usando la división sintética
Ejemplo 1: Dividir el polinomio de abajo.
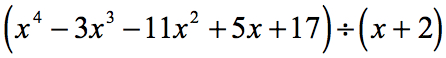
Volvamos a examinar el problema dado y hagamos los ajustes necesarios, si es preciso.
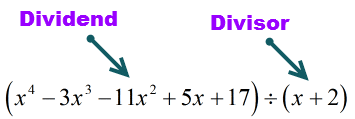
El dividendo (cosa a dividir) está en forma estándar porque los exponentes están en orden decreciente. Eso es bueno!
El divisor necesita ser reescrito como
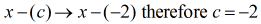
En este punto, ahora puedo establecer la división sintética extrayendo los coeficientes del dividendo y luego alineándolos en la parte superior.
Directamente a la izquierda, coloca el valor de c = – 2 dentro de la «caja».
Por último, construye una línea horizontal justo debajo de los coeficientes del dividendo.
Pasos:
1. Deja caer el primer coeficiente por debajo de la línea horizontal.
2. Multiplica ese número que dejas caer por el número de la «caja». Cualquiera que sea su producto, colócalo encima de la línea horizontal justo debajo del segundo coeficiente.
3. Suma la columna de números, luego pon la suma directamente debajo de la línea horizontal.
4. Repite el proceso hasta que te quedes sin columnas que sumar.
Ve la solución animada a continuación:
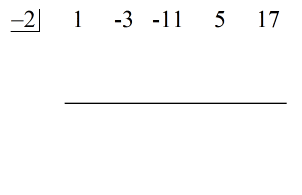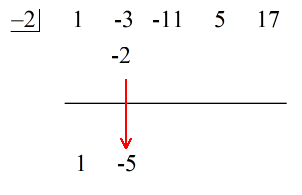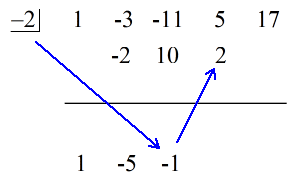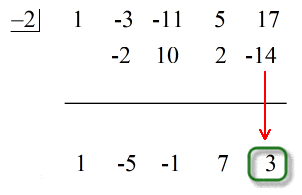
¡El último número debajo de la línea horizontal es siempre el resto! El resto de este problema es 3.
Entonces, ¿cómo presentamos nuestra respuesta final?
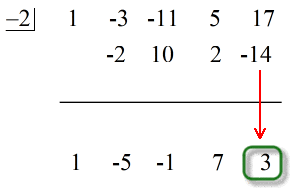
- Muestra tu respuesta final de la forma
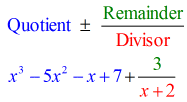
Nota que los números bajo la línea horizontal, excepto el último (resto), son los coeficientes del Cociente.
Más aún, los exponentes de las variables del cociente se reducen todos en 1.
Ejemplo 2: Dividir el polinomio.
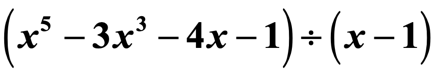
Esta no es una pregunta trampa. Observa que el cociente no tiene todos los exponentes de la variable x.
Veo que nos faltan {x^4} y {x^2}. Para incluir todos los coeficientes de la variable x en potencia decreciente, debemos reescribir el problema original así. Poner ceros en esas x que faltan. Expresar también el divisor como x – (c) lo que revela claramente el valor de c, es decir, c = + 1.
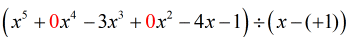
A partir de este punto, ya puedo establecer los números para continuar con el proceso.
Pasos:
1. Deja caer el primer coeficiente por debajo de la línea horizontal.
2. Multiplica ese número que dejas caer por el número de la «caja». Cualquiera que sea su producto, colócalo por encima de la línea horizontal justo debajo del segundo coeficiente.
3. Suma la columna de números, luego pon la suma directamente debajo de la línea horizontal.
4. Repite el proceso hasta que te quedes sin columnas que sumar.
Vea la solución animada a continuación:
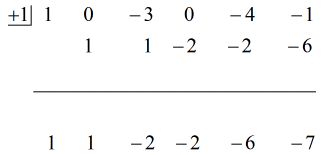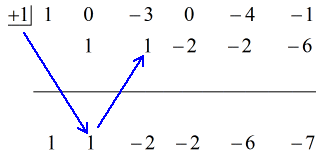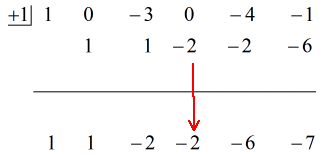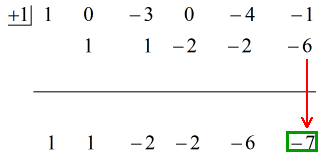
Así que poniendo la respuesta final de la forma
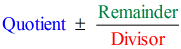
tenemos
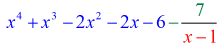
Ejemplo 3: Divide el polinomio de abajo.
Izquierda( { 2{x^4} + x} \a la derecha) \a la izquierda( {x – 3} \a la derecha)
¡Esto se pone más interesante! El cociente definitivamente se ve horrible porque le falta mucho. No sólo le faltan algunas x’s que son {x^3} y {x^2} sino que también ha desaparecido la constante.
Para arreglar esto, reescribiré el problema original de tal manera que todas las x’s estén contabilizadas. Pero lo más importante es no olvidarse de incluir la constante que falta, que es cero.
El problema «nuevo y mejorado» debe quedar así:
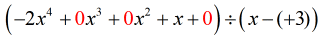
A partir de aquí, proceda con los pasos como siempre.
Pasos:
1. Deja caer el primer coeficiente por debajo de la línea horizontal.
2. Multiplica ese número que dejas caer por el número de la «caja». Cualquiera que sea su producto, colócalo encima de la línea horizontal justo debajo del segundo coeficiente.
3. Suma la columna de números, luego pon la suma directamente debajo de la línea horizontal.
4. Repite el proceso hasta que te quedes sin columnas que sumar.
Veamos la solución animada a continuación:
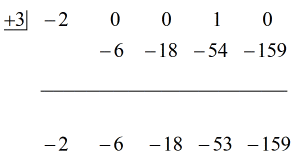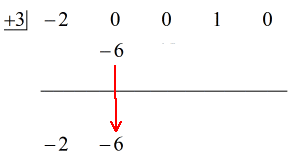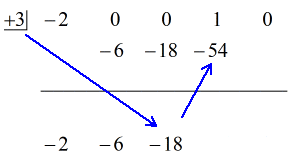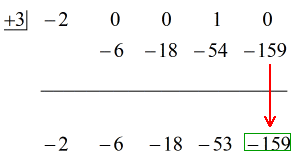
De acuerdo entonces, la respuesta final para esto es
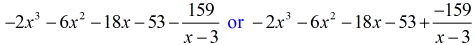
Puedes escribir la respuesta final de dos maneras. La primera es utilizando el símbolo del menos o de la resta para indicar que el resto es negativo. La segunda es utilizando el símbolo + pero adjuntando un símbolo negativo al numerador. Significan lo mismo.
Ejemplo 4: Dividir el polinomio de abajo.
Izquierda( { – {x^5} + 1} \NDerecha) \NIzquierda( {x + 1} \NDerecha)
No te desanimes por este problema. En realidad es bastante fácil, especialmente ahora que ya has pasado por algunos ejemplos. Recuerda siempre «rellenar las partes que faltan», ¿no?
Observa el dividendo y deberías estar de acuerdo en que las partes que faltan son {x^4}, {x^3}, {x^2} y x.
Reescribiendo el problema original que está preparado para la división sintética, obtenemos…
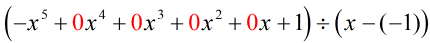
Poblamos las x que faltan con ceros y resolvemos explícitamente para c = -1.
Pasos:
1. Deja caer el primer coeficiente por debajo de la línea horizontal.
2. Multiplica ese número que dejas caer por el número de la «caja». Cualquiera que sea su producto, colócalo por encima de la línea horizontal justo debajo del segundo coeficiente.
3. Suma la columna de números y, a continuación, pon la suma justo debajo de la línea horizontal.
4. Repite el proceso hasta que te quedes sin columnas que sumar.
Ve la solución animada de abajo:
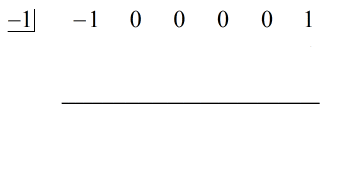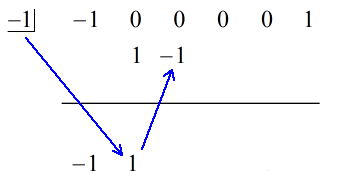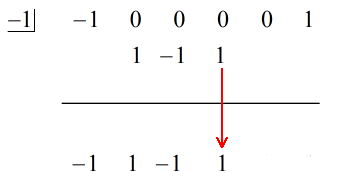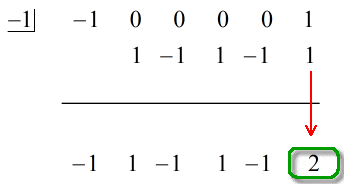
El último número debajo de la línea horizontal siempre será el resto. No lo olvides. En este caso, el resto es igual a 2.
Nuestra respuesta final es
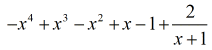
Ejemplo 5: Dividir el polinomio por un binomio.
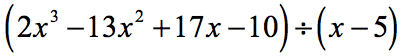
En este ejemplo, obtendremos un resto de cero. Cuando eso ocurre el divisor se convierte en un factor del dividendo. En otras palabras, el divisor divide uniformemente al dividendo.
Examinando el problema, veo que no faltan componentes. Todas las potencias de x están contabilizadas y tenemos una constante. ¡Eso es genial! Este problema está de hecho listo para la división sintética.
Pasos:
1. Deja caer el primer coeficiente por debajo de la línea horizontal.
2. Multiplica ese número que dejas caer por el número de la «caja». Cualquiera que sea su producto, colócalo por encima de la línea horizontal justo debajo del segundo coeficiente.
3. Suma la columna de números, luego pon la suma directamente debajo de la línea horizontal.
4. Repite el proceso hasta que te quedes sin columnas que sumar.
Vea la solución animada a continuación:
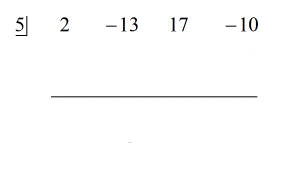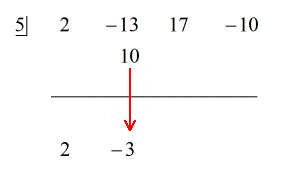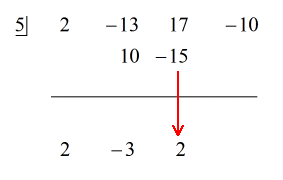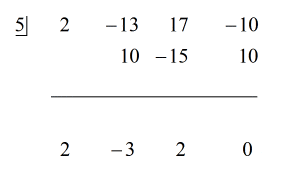
Porque el resto es igual a cero, esto significa que el divisor x – 5 es un factor del dividendo
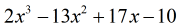
por tanto
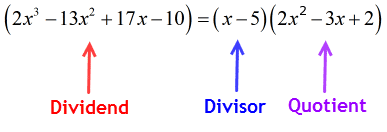
Practica con las hojas de trabajo
También te puede interesar:
Suma y resta de polinomios
División de polinomios por el método de la división larga
Multiplicación de binomios por el método FOIL
Multiplicación de polinomios




