Propiedades de los cuadriláteros – Rectángulo, Cuadrado, Paralelogramo, Rombo, Trapecio
En la geometría euclidiana, un cuadrilátero es una figura 2D de cuatro lados cuya suma de ángulos internos es de 360°. La palabra cuadrilátero deriva de dos palabras latinas «quadri» y «latus» que significan cuatro y lado respectivamente. Por lo tanto, identificar las propiedades de los cuadriláteros es importante cuando se trata de distinguirlos de otros polígonos.
Entonces, ¿cuáles son las propiedades de los cuadriláteros? Hay dos propiedades de los cuadriláteros:
- Un cuadrilátero debe ser una forma cerrada con 4 lados
- Todos los ángulos internos de un cuadrilátero suman 360°
En este artículo, tendrás una idea sobre los 5 tipos de cuadriláteros y conocerás las propiedades de los cuadriláteros.
Esto es lo que leerás en el artículo:
- Diferentes tipos de cuadriláteros
- Rectángulo
- Propiedades de los rectángulos
- Fórmulas de los rectángulos
- Cuadrado
- Propiedades de un cuadrado
- Fórmulas de cuadrados
- Paralelogramo
- Propiedades de los paralelogramos
- Fórmulas del paralelogramo
- Rombo
- Propiedades de un rombo
- Fórmulas del rombo
- Trapecio/Trapezoide
- Propiedades de un trapecio
- Fórmulas del trapecio
- Propiedades de los cuadriláteros
- Fórmulas importantes de los cuadriláteros
- Preguntas sobre cuadriláteros
Aquí tienes un vídeo que explica las propiedades de los cuadriláteros:
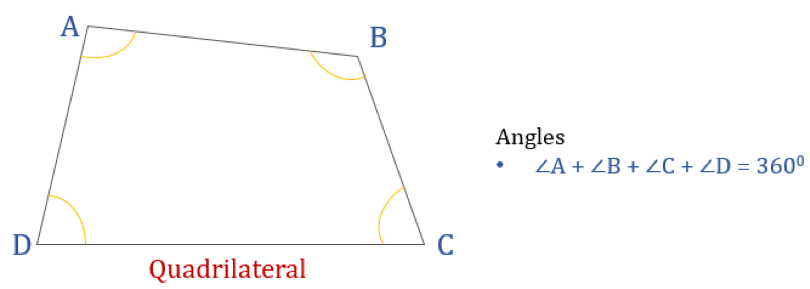
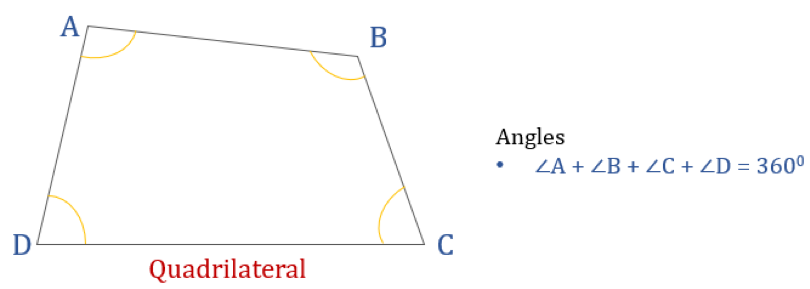
El diagrama dado a continuación muestra un cuadrilátero ABCD y la suma de sus ángulos internos. Todos los ángulos internos suman 360°.
Por tanto, ∠A + ∠B + ∠C + ∠D = 360°
Diferentes tipos de cuadriláteros
Hay 5 tipos de cuadriláteros en función de su forma. Estos 5 cuadriláteros son:
- Rectángulo
- Cuadrado
- Paralelogramo
- Rombo
- Trapecio
Discutiremos cada uno de estos 5 cuadriláteros en detalle:
Aquí tienes preguntas que te enseñarán a aplicar las propiedades de los 5 cuadriláteros que aprenderás en este artículo.
Rectángulo
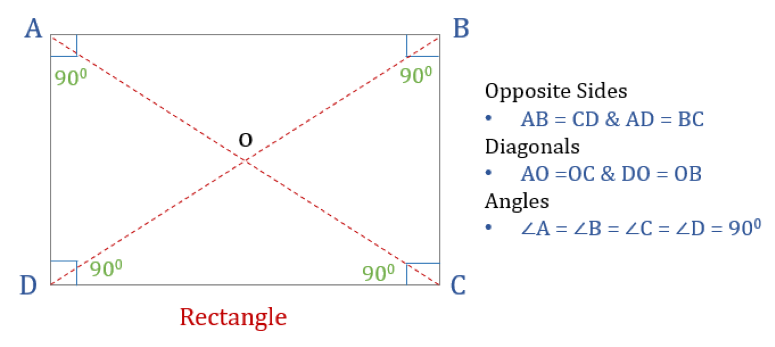
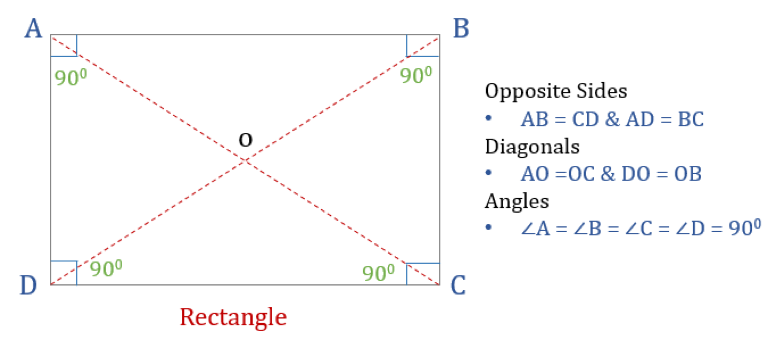
Un rectángulo es un cuadrilátero con cuatro ángulos rectos. Por tanto, todos los ángulos de un rectángulo son iguales (360°/4 = 90°). Además, los lados opuestos de un rectángulo son paralelos e iguales, y las diagonales se bisecan entre sí.
Propiedades de los rectángulos
Un rectángulo tiene tres propiedades:
- Todos los ángulos de un rectángulo son de 90°
- Los lados opuestos de un rectángulo son iguales y Paralelos
- Los diagonales de un rectángulo se bisecan entre sí
Fórmula del rectángulo – Área y perímetro de un rectángulo
Si la longitud del rectángulo es L y la anchura es B entonces,
- Área de un rectángulo = Longitud × Anchura o L × B
- Perímetro del rectángulo = 2 × (L + B)
Estas preguntas de práctica te ayudarán a consolidar las propiedades de los rectángulos
Cuadrado
El cuadrado es un cuadrilátero con cuatro lados y ángulos iguales. También es un cuadrilátero regular ya que tanto sus lados como sus ángulos son iguales. Al igual que un rectángulo, un cuadrado tiene cuatro ángulos de 90° cada uno. También puede verse como un rectángulo cuyos dos lados adyacentes son iguales.
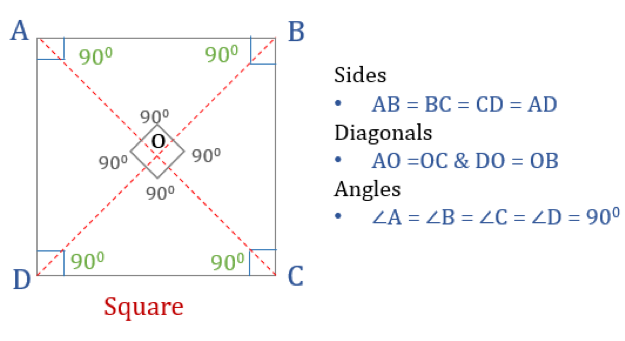
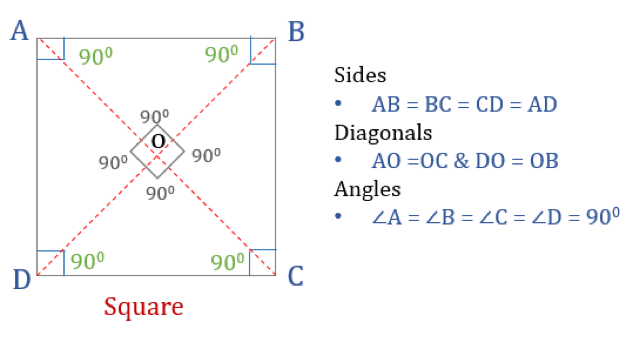
Propiedades de un cuadrado
Para que un cuadrilátero sea un cuadrado, tiene que tener ciertas propiedades. Aquí tienes las tres propiedades de los cuadrados:
- Todos los ángulos de un cuadrado son de 90°
- Todos los lados de un cuadrado son iguales y paralelos entre sí
- Los diagonales se bisecan perpendicularmente
Fórmula del cuadrado – Área y perímetro de un cuadrado
Si el lado de un cuadrado es ‘a’ entonces,
- Área del cuadrado = a × a = a²
- Perímetro del cuadrado = 2 × (a + a) = 4a
Estas preguntas de práctica te ayudarán a consolidar las propiedades de los cuadrados
Conseguir una Q50-51 en el GMAT te ayuda a obtener una puntuación superior a 700 en el GMAT. Por qué no empiezas a prepararte para el GMAT con nuestros recursos de preparación gratuitos y comienzas tu camino para conseguir una Q50-51 en el GMAT. Aprende de Carrie Law que mejoró de Q35 a Q50 en 3 semanas.
Paralelogramo
Un paralelogramo, como su nombre indica, es un cuadrilátero simple cuyos lados opuestos son paralelos. Por tanto, tiene dos pares de lados paralelos. Además, los ángulos opuestos en un paralelogramo son iguales y sus diagonales se bisecan entre sí.
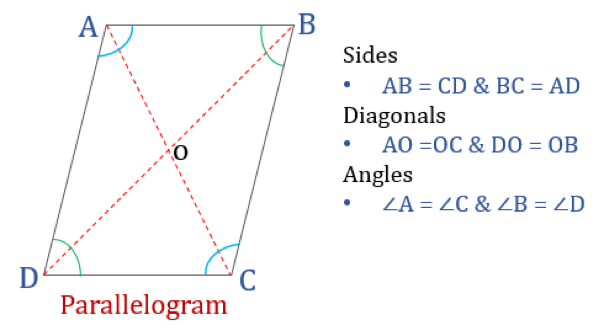
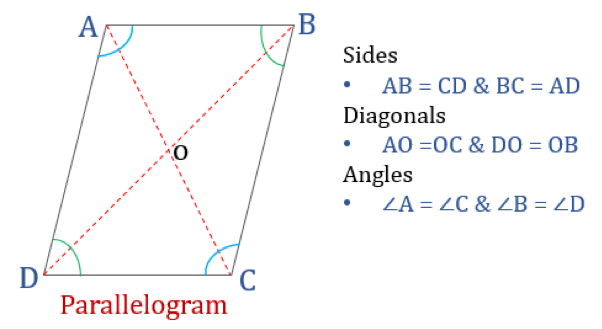
Propiedades del paralelogramo
Un cuadrilátero que satisfaga las propiedades mencionadas a continuación se clasificará como paralelogramo. Un paralelogramo tiene cuatro propiedades:
- Los ángulos opuestos son iguales
- Los lados opuestos son iguales y paralelos
- Los diagonales se bisecan
- La suma de dos ángulos adyacentes cualesquiera es 180°
Fórmulas del paralelogramo – Área y perímetro de un paralelogramo
Si la longitud de un paralelogramo es ‘l’, la anchura es ‘b’ y la altura es ‘h’ entonces:
- Perímetro del paralelogramo= 2 × (l + b)
- Área del paralelogramo = l × h
Estas preguntas de práctica te ayudarán a solidificar las propiedades del paralelogramo
Rombo
Un rombo es un cuadrilátero cuyos cuatro lados son iguales en longitud y los lados opuestos son paralelos entre sí. Sin embargo, los ángulos no son iguales a 90°. Un rombo con ángulos rectos sería un cuadrado. Otro nombre para el rombo es «diamante», ya que su aspecto es similar al del palo de diamante en los naipes.
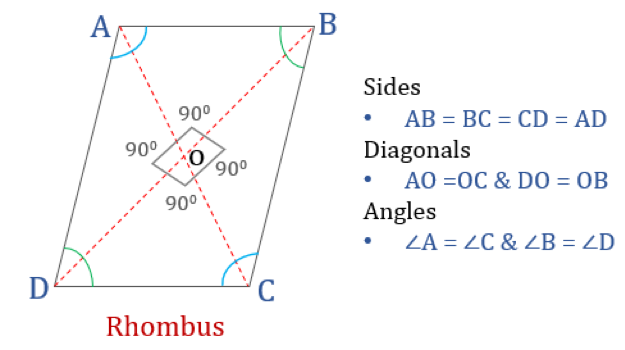
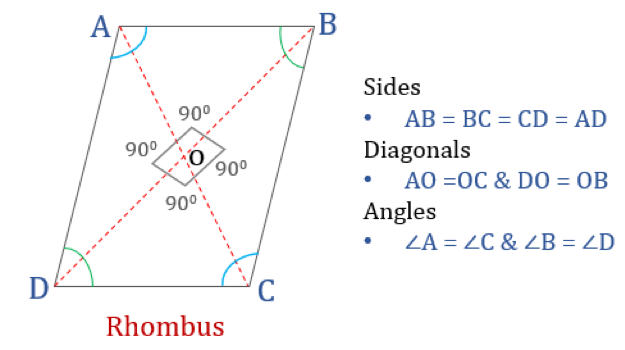
Propiedades del rombo
Un rombo es un cuadrilátero que tiene las siguientes cuatro propiedades:
- Los ángulos opuestos son iguales
- Todos los lados son iguales y, los lados opuestos son paralelos entre sí
- Los diagonales se bisecan perpendicularmente
- La suma de dos ángulos adyacentes cualesquiera es 180°
Fórmulas del rombo – Área y perímetro de un rombo
Si el lado de un rombo es a entonces, perímetro de un rombo = 4a
Si la longitud de dos diagonales del rombo es d1 y d2 entonces el área de un rombo = ½ × d1 × d2
Estas preguntas de práctica te te ayudarán a afianzar las propiedades del rombo
Trapecio
Un trapecio (llamado Trapezoide en EEUU) es un cuadrilátero que tiene sólo un par de lados paralelos. Los lados paralelos se denominan «bases» y los otros dos lados se llaman «catetos» o lados laterales.
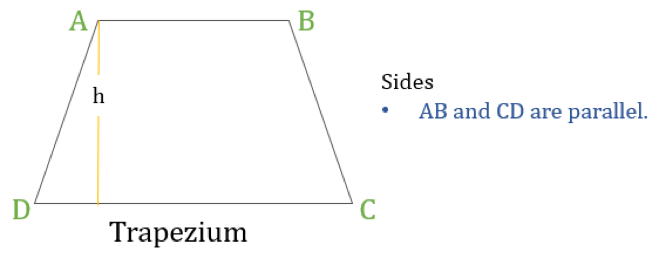
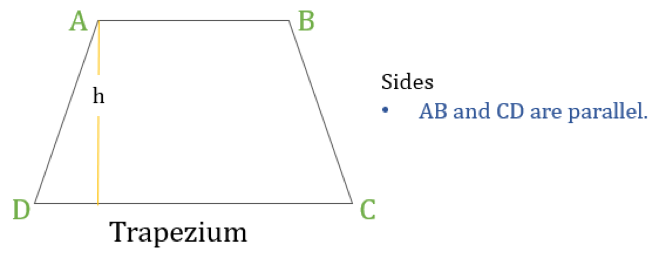
Propiedades del trapecio
Un trapecio es un cuadrilátero en el que se da la siguiente propiedad:
- Sólo un par de lados opuestos son paralelos entre sí
Fórmulas del trapecio – Área y perímetro de un trapecio
Si la altura de un trapecio es ‘h’ (como se muestra en el diagrama anterior) entonces:
- Perímetro del trapecio= Suma de las longitudes de todos los lados = AB + BC + CD + DA
- Área del trapecio = ½ × (Suma de las longitudes de los lados paralelos) × h = ½ × (AB + CD) × h
Estas preguntas de práctica te ayudarán a afianzar las propiedades del trapecio
Propiedades de los cuadriláteros
La siguiente tabla resume todas las propiedades de los cuadriláteros que hemos aprendido hasta ahora:
| Propiedades de los cuadriláteros | Rectángulo | Cuadrado | Paralelogramo | Rombo | Trapecio |
| Todos los lados son iguales | ✖ | ✔ | ✖ | ✔ | ✖ |
| Opuestos Los lados son iguales | ✔ | ✔ | ✔ | ✔ | ✖ |
| Los lados son paralelos | ✔ | ✔ | ✔ | ✔ | ✔ |
| Todos los ángulos son iguales | ✔ | ✔ | ✖ | ✖ | ✖ |
| Los ángulos opuestos son iguales | ✔ | ✔ | ✔ | ✔ | |
| La suma de dos ángulos adyacentes es 180 | ✔ | ✔ | ✔ | ✔ | ✖ |
| Se disecan entre sí | ✔ | ✔ | ✔ | ✔ | ✖ |
| Se disecan perpendicularmente | ✖ | ✔ | ✖ | ✔ | ✖ |
La siguiente imagen también resume las propiedades de los cuadriláteros:
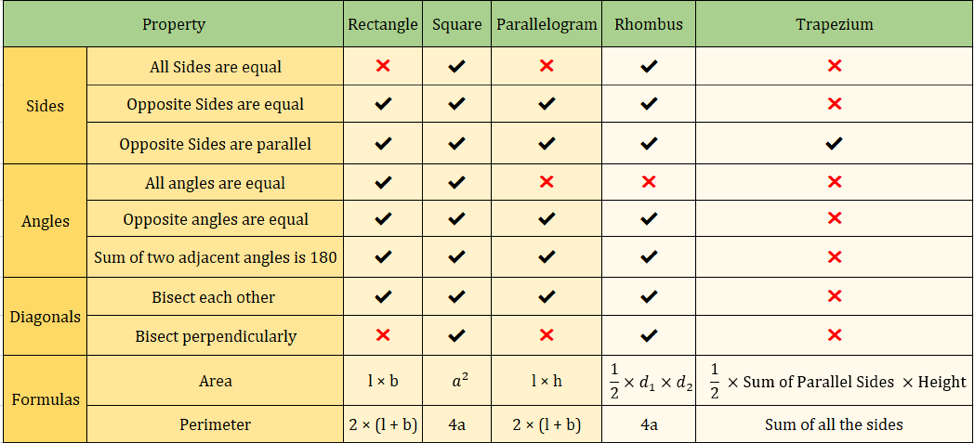
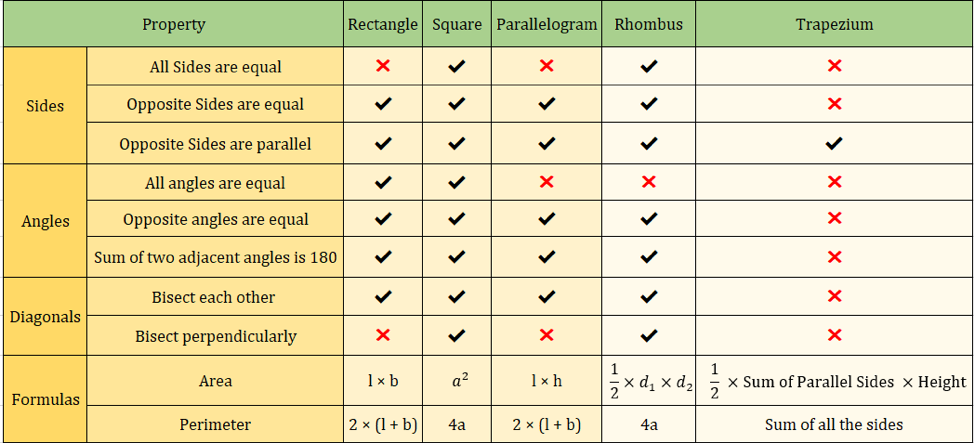
Fórmulas importantes de los cuadriláteros
La siguiente tabla resume las fórmulas de área y perímetro de los diferentes tipos de cuadriláteros:
| Fórmulas de cuadriláteros | Rectángulo | Cuadrado | Paralelogramo | Rombo | Trapecio |
| Área | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Suma de lados paralelos) × altura |
| Perímetro | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Suma de todos los lados |
Lectura adicional:
- Propiedades del Círculo | Fórmulas del Círculo – Área y Perímetro
- Propiedades de los Números – Pares & Impares | Primas | HCF & LCM
- Propiedades de los Triángulos – Definición | Tipos |. Clasificación
- Líneas y ángulos – Propiedades y su aplicación
Preguntas de cuadriláteros
Practiquemos la aplicación de las propiedades de los cuadriláteros en las siguientes preguntas de ejemplo:
Pregunta 1
Adán quiere construir una valla alrededor de su jardín rectangular de 10 metros de largo y 15 de ancho. ¿Cuántos metros de valla debe comprar para cercar todo el jardín?
- 20 metros
- 25 metros
- 30 metros
- 40 metros
- 50 metros
Solución
Paso 1: Dado
- Adam tiene un jardín rectangular.
- Tiene una longitud de 10 metros y una anchura de 15 metros.
- Quiere construir una valla alrededor del mismo.
Paso 2: Hallar
- La longitud necesaria para construir la valla alrededor de todo el jardín.
Paso 3: Aproximación y elaboración
La valla sólo puede construirse alrededor de los lados exteriores del jardín.
- Por tanto, la longitud total de la valla necesaria= Suma de las longitudes de todos los lados del jardín.
- Como el jardín es rectangular, la suma de las longitudes de todos los lados no es más que el perímetro del jardín.
- Perímetro = 2 × (10 + 15) = 50 metros
Por tanto, la longitud necesaria de la valla es de 50 metros.
Por tanto, la opción E es la respuesta correcta.
Pregunta: 2
Steve quiere pintar una pared de forma rectangular de su habitación. El coste de pintar la pared es de 1,5 dólares por metro cuadrado. Si la pared tiene 25 metros de largo y 18 metros de ancho, entonces ¿cuál es el coste total de pintar la pared?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Solución
Paso 1: Dado
- Steve quiere pintar una pared de su habitación.
- La pared tiene 25 metros de largo y 18 de ancho.
- El coste de pintar la pared es de 1,5 dólares por metro cuadrado.
Paso 2: Hallar
- El coste total de pintar la pared.
Paso 3: Planteamiento y elaboración
- Se pinta una pared en toda su superficie.
- Entonces, si hallamos el área total de la pared en metros cuadrados y la multiplicamos por el costo de pintar 1 metro cuadrado de la pared entonces podemos el costo total.
- Área de la pared = largo × ancho = 25 metros × 18 metros = 450 metros cuadrados
- Costo total de pintar la pared = 450 × $1.5 = $675
Por lo tanto, la respuesta correcta es la opción E.
Esperamos que a estas alturas hayas aprendido los diferentes tipos de cuadriláteros, sus propiedades y fórmulas y cómo aplicar estos conceptos para resolver preguntas sobre cuadriláteros. La aplicación de los cuadriláteros es importante para resolver las preguntas de geometría en el GMAT. Si estás planeando hacer el GMAT, podemos ayudarte con material de estudio de alta calidad al que puedes acceder gratuitamente registrándote aquí.
Aquí hay algunos artículos más sobre Matemáticas:
- Mejora la precisión en las preguntas de Matemáticas sobre Polígonos
- Preguntas de Geometría – Errores más comunes | GMAT Quant Prep
Si estás planeando hacer el GMAT, podemos darte acceso a contenido online de calidad para prepararte. Somos la empresa de preparación para el GMAT con más reseñas en gmatclub con más de 1950 reseñas.
¿Por qué no haces una prueba gratuita y juzgas por ti mismo?
Escríbenos a [email protected] en caso de cualquier consulta.




