Skewness – Introducción rápida, ejemplos y fórmulas
Skewness es un número que indica hasta qué punto
una variable está distribuida asimétricamente.
- Ejemplo de asimetría positiva (derecha)
- Ejemplo de asimetría negativa (izquierda)
- Asimetría de la población – Fórmula y cálculo
- Asimetría de la muestra -. Fórmula y cálculo
- Porcentaje de asimetría en el SPSS
- Porcentaje de asimetría – Implicaciones para el análisis de datos
Ejemplo de asimetría positiva (derecha)
Un científico hace que 1,000 personas completen algunas pruebas psicológicas. Para el test 5, las puntuaciones del test tienen una asimetría = 2,0. A continuación se muestra un histograma de estas puntuaciones.
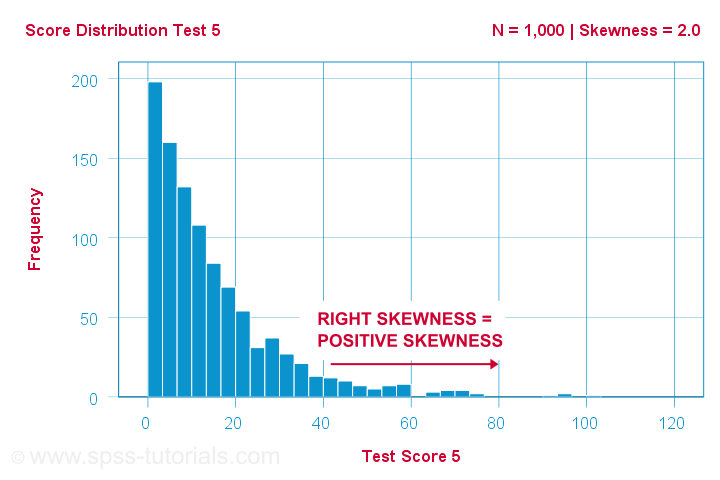
El histograma muestra una distribución de frecuencias muy asimétrica. La mayoría de las personas obtienen 20 puntos o menos, pero la cola derecha se extiende hasta 90 aproximadamente. Esta distribución está sesgada a la derecha.
Si nos movemos hacia la derecha a lo largo del eje x, pasamos de 0 a 20 a 40 puntos y así sucesivamente. Así que hacia la derecha del gráfico, las puntuaciones se vuelven más positivas. Por lo tanto, la asimetría derecha es asimetría positiva, lo que significa asimetría > 0. Este primer ejemplo tiene asimetría = 2,0 como se indica en la esquina superior derecha del gráfico. Las puntuaciones están fuertemente sesgadas positivamente.
Ejemplo de asimetría negativa (izquierda)
Otra variable -las puntuaciones de la prueba 2- resultan tener asimetría = -1,0. Su histograma se muestra a continuación.

El grueso de las puntuaciones está entre 60 y 100 aproximadamente. Sin embargo, la cola izquierda se estira un poco. Así que esta distribución es sesgada a la izquierda.
Derecha: a la izquierda, a la izquierda. Si seguimos el eje x hacia la izquierda, nos movemos hacia puntuaciones más negativas. Por eso la asimetría izquierda es asimetría negativa.Y efectivamente, asimetría = -1,0 para estas puntuaciones. Su distribución está sesgada a la izquierda. Sin embargo, está menos sesgada -o es más simétrica- que nuestro primer ejemplo, que tenía una asimetría = 2,0.
La distribución simétrica implica una asimetría cero
Por último, las distribuciones simétricas tienen una asimetría = 0. Las puntuaciones de la prueba 3 -que tienen una asimetría = 0,1- se aproximan.

Ahora bien, las distribuciones observadas rara vez son precisamente simétricas. Esto se observa sobre todo en algunas distribuciones muestrales teóricas. Algunos ejemplos son
- la distribución normal (estándar);
- la distribución t y
- la distribución binomial si p = 0,5.
Todas estas distribuciones son exactamente simétricas y por lo tanto tienen asimetría = 0.000…
Distribución de la población – Fórmula y cálculo
Si desea calcular las asimetrías de una o más variables, deje los cálculos a algún software. Pero -sólo para completar- enumeraré las fórmulas de todos modos.
Si sus datos contienen toda la población, calcule la asimetría de la población como:
$$Population\\\\N;skewness = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$
donde
- (X_i\) es cada puntuación individual;
- (\mu\) es la media de la población;
- (\sigma\) es la desviación estándar de la población y
- (N\) es el tamaño de la población.
Para un ejemplo de cálculo utilizando esta fórmula, véase esta hoja de Google (que se muestra a continuación).
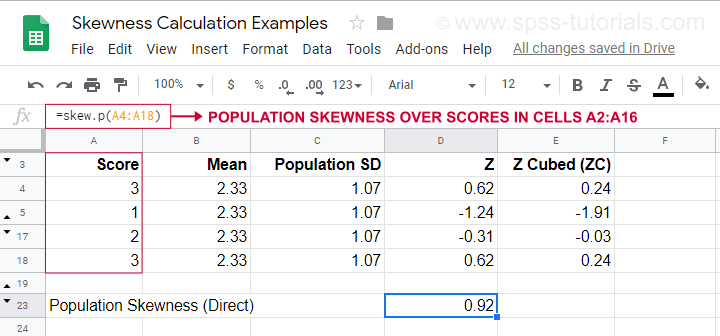
También muestra cómo obtener la asimetría de la población directamente utilizando=SKEW.P(…)donde «.P» significa «población». Esto confirma el resultado de nuestro cálculo manual. Lamentablemente, ni SPSS ni JASP calculan la asimetría poblacional: ambos se limitan a la asimetría muestral.
Espesor de la muestra – Fórmula y cálculo
Si sus datos contienen una muestra aleatoria simple de alguna población, utilice
$$Muestraskewness = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$
donde
- (X_i\) es cada puntuación individual;
- (\\ sobreX}) es la media de la muestra;
- (S\) es la desviación estándar de la muestra y
- (N\) es el tamaño de la muestra.
Un ejemplo de cálculo se muestra en esta Googlesheet (que se muestra a continuación).
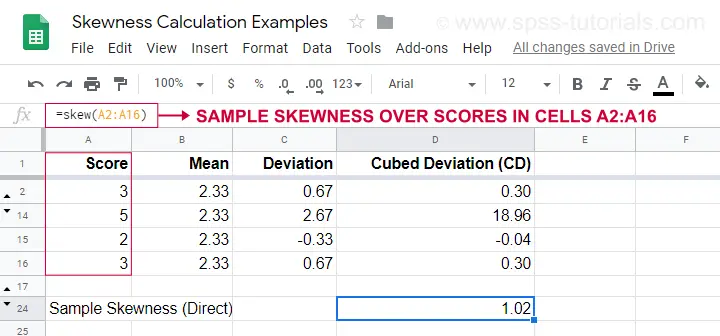
Una opción más sencilla para obtener la asimetría de la muestra es utilizar=SKEW(…).que confirma el resultado de nuestro cálculo manual.
La asimetría en SPSS
En primer lugar, la «asimetría» en SPSS siempre se refiere a la asimetría de la muestra: asume tranquilamente que sus datos contienen una muestra y no una población entera. Hay muchas opciones para obtenerla. Mi favorita es a través de MEANS porque la sintaxis y la salida son limpias y simples. Las capturas de pantalla a continuación le guían.

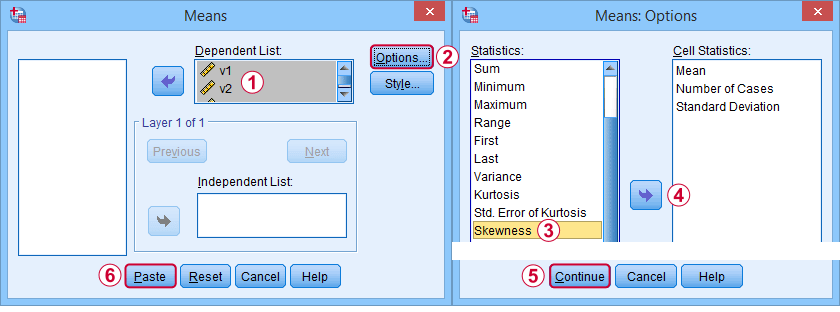
La sintaxis puede ser tan simple comomeans v1 a v5
/cells skew.Una tabla muy completa -incluyendo medias, desviaciones estándar, medianas y más- se ejecuta desdemeans v1 a v5
/cells count min max mean median stddev skew kurt.El resultado se muestra a continuación.
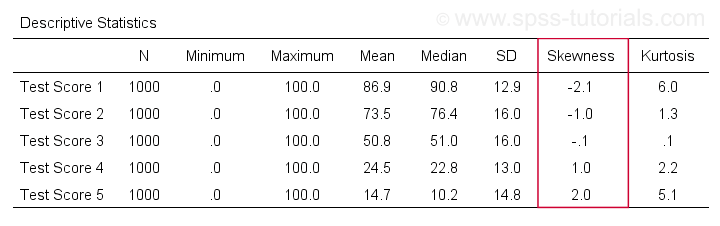
La asimetría – Implicaciones para el análisis de datos
Muchos análisis -ANOVA, pruebas t, regresión y otros- requieren el supuesto de normalidad: las variables deben distribuirse normalmente en la población. La distribución normal tiene una asimetría = 0. Por lo tanto, la observación de una asimetría sustancial en algunos datos de la muestra sugiere que se viola el supuesto de normalidad.
Estas violaciones de la normalidad no son un problema para tamaños de muestra grandes -por ejemplo, N > 20 o 25 más o menos. En este caso, la mayoría de las pruebas son robustas contra tales violaciones. Esto se debe al teorema del límite central. En resumen, para tamaños de muestra grandes, la asimetría no es un problema real para las pruebas estadísticas. Esto puede dar lugar a grandes errores estándar y a una baja potencia estadística. Así, una asimetría sustancial puede disminuir la posibilidad de rechazar alguna hipótesis nula para demostrar algún efecto. En este caso, una prueba no paramétrica puede ser una opción más sabia, ya que puede tener más potencia.Las violaciones de la normalidad suponen una amenaza real
para tamaños de muestra pequeños de -por ejemplo- N < 20 o así. Con tamaños de muestra pequeños, muchas pruebas no son robustas frente a una violación del supuesto de normalidad. La solución -una vez más- es utilizar una prueba no paramétrica porque éstas no requieren normalidad.
Por último, pero no menos importante, no hay ninguna prueba estadística para examinar si la asimetría de la población = 0. Una forma indirecta de probar esto es una prueba de normalidad como
- la prueba de normalidad de Kolmogorov-Smirnov y
- la prueba de normalidad de Shapiro-Wilk.
Sin embargo, cuando la normalidad es realmente necesaria -con tamaños de muestra pequeños- estas pruebas tienen poca potencia: pueden no alcanzar la significación estadística incluso cuando las desviaciones de la normalidad son graves. De este modo, proporcionan principalmente una falsa sensación de seguridad.




