Aaltofunktion määritelmä
Fundamenttihiukkasia, kuten elektroneja, voidaan kuvata hiukkasina tai aaltoina.
Elektroneita voidaan kuvata aaltofunktion avulla.aaltofunktion symboli on kreikkalainen kirjain ps, Ψ tai ψ.

Aaltofunktio Ψ on matemaattinen lauseke.Se kuljettaa ratkaisevaa tietoa elektronista, johon se liittyy:aaltofunktiosta saadaan elektronin energia, kulmavoima ja orbitaalien suuntaus kvanttilukujen n, l ja ml muodossa.
Aaltofunktiolla voi olla positiivinen tai negatiivinen merkki.merkki on tärkeä laskutoimituksissa.sillä on merkitystä myös silloin, kun kahden tai useamman atomin aaltofunktiot yhdistyvät muodostaen molekyylin.
Aaltofunktiot, joilla on samanlaiset merkit (aallot ovat samassa vaiheessa), interferoivat rakentavasti, mikä johtaa sidoksen syntymiseen.Aaltofunktiot, joilla on erilaiset merkit (aallot ovat erivaiheisia), interferoivat tuhoavasti.
Ervin Schrödinger päätteli vuonna 1926 aaltofunktion yksinkertaisimmalle kaikista atomeista, vedylle.Schrödingerin yhtälön ratkaiseminen antaa tutkijoille mahdollisuuden määritellä aaltofunktiot atomeissa ja molekyyleissä oleville elektroneille.
Schrödingerin yhtälö on kvanttimekaniikan yhtälö: lasketuilla aaltofunktioilla on diskreetit, sallitut arvot atomeihin ja molekyyleihin sitoutuneille elektroneille;kaikki muut arvot ovat kiellettyjä.
Ps:n merkityksen lisäksi sen neliöllä Ψ2 on valtava merkitys kemiassa.
Ψ2 on todennäköisyystiheys.se kertoo, missä elektroni todennäköisimmin sijaitsee ydintä ympäröivässä avaruudessa.
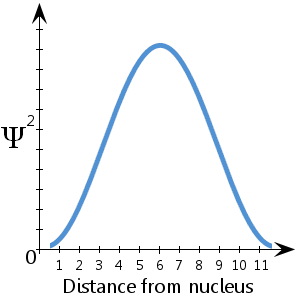
Esimerkiksi tässä piirretyssä (kuvitteellisessa) kaaviossa, jossa Ψ2 on esitetty etäisyyden suhteen ytimestä, näemme, että elektroni on todennäköisimmin noin 5-7 yksikön etäisyydellä ytimestä.Näemme myös, että on häviävän pieni todennäköisyys, että elektroni on ytimen kohdalla tai yli 11½ yksikön päässä ytimestä.
On 100 prosentin todennäköisyys, että elektroni on jossain – toisin sanoen todennäköisyys on 1.
Ψ voidaan laskea tarkasti vain atomeille, joilla on yksi elektroni, eli H, He+, Li2+, Be3+, B4+, C5+ jne.Matemaattisella kielellä sanomme, että Ψ:n analyyttiset ratkaisut ovat mahdollisia vain yhden elektronin systeemeille.Yhden elektronin systeemejä kuvataan usein vetyvaikutteisiksi – mikä tarkoittaa ”kuten vety”.”
Kaikille muille atomeille, ioneille ja molekyyleille Ψ:n analyyttiset ratkaisut eivät ole mahdollisia;sen laskemiseen tarvitaan approksimaatiomenetelmiä.
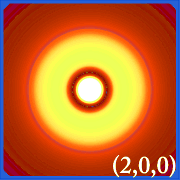
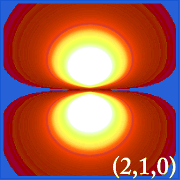
Ψ2 ja vetyperäiset orbitaalit
Kuvaamalla vedyn todennäköisyystiheyttä (i.eli Ψ2) eri kvanttiluvuilla antaa meille mahdollisuuden havainnollistaa ytimeen keskitetyn tilan, jonka elektronit valtaavat.Erilaiset Ψ2-jakaumat ovat vedyn elektroniorbitaaleja.Se, mikä orbitaali on todellisuudessa miehitetty, määräytyy sen mukaan, kuinka paljon energiaa elektronilla on.
Esimerkkejä vedyn orbitaaleista