Algebran alkeet
Oppimistavoitteet
- Järjestettyjen parien piirtäminen
- Koordinaattitason komponenttien tunnistaminen
- Plottaa järjestettyjä pareja koordinaattitasossa
- Tunnistaa koordinaattitason kvadrantteja
- Tunnistaa koordinaattitason neljä kvadranttia
- Anna järjestetty pari, määritä sen kvadrantti
Koordinaattitason kehitti vuosisatoja sitten (tarkalleen ottaen vuonna 1637) ranskalainen matemaatikko René Descartes. Hänen kunniakseen järjestelmää kutsutaan joskus kartesiolaiseksi koordinaatistoksi. Koordinaattitasoa voidaan käyttää pisteiden piirtämiseen ja viivojen kuvaamiseen. Tämän järjestelmän avulla voimme kuvata algebrallisia suhteita visuaalisesti, ja se auttaa meitä myös luomaan ja tulkitsemaan algebrallisia käsitteitä.
Koordinaattitason komponentit
Olet todennäköisesti käyttänyt koordinaattitasoa ennenkin. Oletko esimerkiksi koskaan käyttänyt rasteripeittoa kartoittaaksesi jonkin esineen sijainnin? (Näin tehdään usein myös tiekartoissa.)

Tässä ”kartassa” käytetään vaaka- ja pystysuuntaista ruudukkoa välittämään tietoa kohteen sijainnista. Huomaa, että kirjaimet A-F on lueteltu yläreunassa ja numerot 1-6 vasemmassa reunassa. Minkä tahansa kohteen yleinen sijainti tällä kartalla voidaan löytää käyttämällä sen ruudukon kirjainta ja numeroa. Löydät esimerkiksi kohteen, joka on ruudussa ”4F”, siirtämällä sormesi vaakasuoraa pitkin kirjaimeen F ja sitten suoraan alaspäin niin, että olet linjassa 4:n kanssa. Löydät sinisen kiekon, joka on tässä kohdassa karttaa.
Koordinaattitasossa on samanlaisia elementtejä kuin edellä esitetyssä ruudukossa. Se koostuu vaaka- ja pystyakselista, numeroviivoista, jotka leikkaavat toisensa suorassa kulmassa. (Ne ovat kohtisuorassa toisiaan vastaan.)
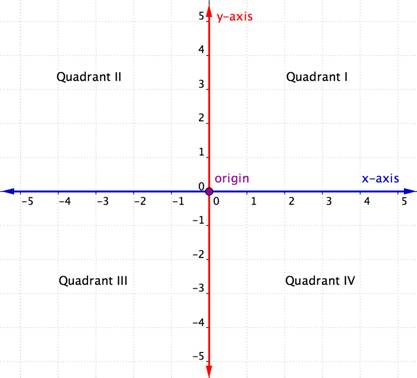
Koordinaattitason vaaka-akselia kutsutaan x-akseliksi. Pystyakselia kutsutaan y-akseliksi. Pistettä, jossa nämä kaksi akselia leikkaavat toisensa, kutsutaan origoksi. Alkupiste on x-akselilla kohdassa 0 ja y-akselilla kohdassa 0.
Koordinaattitason paikat kuvataan järjestettyinä pareina. Järjestetty pari kertoo pisteen sijainnin suhteuttamalla pisteen sijainnin x-akselilla (järjestetyn parin ensimmäinen arvo) ja y-akselilla (järjestetyn parin toinen arvo).
Jossain järjestetyssä parissa, kuten (x, y), ensimmäistä arvoa kutsutaan x-koordinaatiksi ja toista arvoa y-koordinaatiksi. Huomaa, että x-koordinaatti luetellaan ennen y-koordinaattia. Koska origon x-koordinaatti on 0 ja y-koordinaatti 0, sen järjestetty pari kirjoitetaan (0, 0).
Harkitse alla olevaa pistettä.

Tunnistaaksesi tämän pisteen sijainnin, aloita origosta (0, 0) ja siirry x-akselia pitkin oikealle, kunnes olet pisteen alla. Katso x-akselilla olevaa merkintää. Merkintä 4 osoittaa, että olet kulkenut origosta neljä yksikköä x-akselia pitkin oikealle. Tämä on x-koordinaatti, järjestetyn parin ensimmäinen numero.
Siirry x-akselilla olevasta 4:stä ylöspäin pisteeseen ja huomaa, minkä numeron kanssa se on linjassa y-akselilla. 3 osoittaa, että x-akselilta lähdettyäsi matkustit 3 yksikköä ylöspäin pystysuunnassa, y-akselin suunnassa. Tämä luku on y-koordinaatti, järjestetyn parin toinen luku. Kun x-koordinaatti on 4 ja y-koordinaatti 3, sinulla on järjestetty pari (4, 3).
Katsotaan toinen esimerkki.
Esimerkki
Kuvaa esitetty piste järjestettynä parina.

Kuvaa järjestettynä parina esitetty piste
Pisteiden piirtäminen koordinaattitasossa
Nyt kun osaat käyttää x- ja y-akseleita, voit piirtää myös järjestetyn parin. Muista vain, että molemmat prosessit alkavat origosta – alusta! Seuraavassa esimerkissä näytetään, miten järjestetyn parin (1,3) kuvaaja piirretään.
Esimerkki
Piirrä piste (1, 3).
Edellisessä esimerkissä sekä x- että y-koordinaatit olivat positiivisia. Kun järjestetyn parin toinen (tai molemmat) koordinaatit ovat negatiivisia, sinun on liikuttava negatiiviseen suuntaan toista tai molempia akseleita pitkin. Tarkastellaan alla olevaa esimerkkiä, jossa molemmat koordinaatit ovat negatiivisia.
Esimerkki
Piirrä piste (-4,-2).

X-koordinaatti on -4, koska se on järjestetyssä parissa ensimmäisenä. Aloitetaan origosta ja siirretään x-akselia pitkin 4 yksikköä negatiiviseen suuntaan (vasemmalle).
Y-koordinaatti on -2, koska se on järjestetyssä parissa toisena. Siirry nyt 2 yksikköä negatiiviseen suuntaan (alaspäin). Jos katsot y-akselille, sinun pitäisi olla linjassa -2:n kanssa kyseisellä akselilla.
Pisteen piirtämisen vaiheet on tiivistetty alla.
Vaiheet järjestetyn parin (x, y) piirtämiseen koordinaattitasossa
- Määritä x-koordinaatti. Siirry origosta alkaen vaakasuoraan x-akselin suuntaan x-koordinaatin antaman matkan verran. Jos x-koordinaatti on positiivinen, liikutaan oikealle; jos x-koordinaatti on negatiivinen, liikutaan vasemmalle.
- Määritä y-koordinaatti. Siirry x-koordinaatista alkaen pystysuoraan y-akselin suuntaan y-koordinaatin antaman matkan verran. Jos y-koordinaatti on positiivinen, liikutaan ylöspäin; jos y-koordinaatti on negatiivinen, liikutaan alaspäin.
- Piirrä piste päätepisteeseen. Merkitse piste järjestetyllä parilla.
Pisteiden piirtäminen koordinaattitasolle
Tunnista kvadrantit ja käytä niitä pisteiden piirtämiseen
Koordinaattitason leikkaavat x- ja y-akselit jakavat sen neljään osaan. Näitä neljää jaksoa kutsutaan kvadranteiksi. Kvadrantit nimetään roomalaisin numeroin I, II, III ja IV alkaen oikeasta yläneljänneksestä ja kulkien vastapäivään.
Jossain tietyssä kvadrantissa olevilla järjestetyillä pareilla on tiettyjä yhteisiä ominaisuuksia. Katso kutakin kvadranttia alla olevassa kuvaajassa. Mitä huomaat kunkin kvadrantin sisällä olevien pisteiden x- ja y-koordinaattien merkeissä?
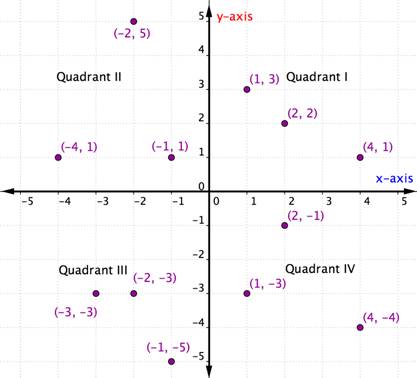
Kunkin kvadrantin sisällä kunkin järjestetyn parin x- ja y-koordinaattien merkit ovat samat. Ne noudattavat myös kaavaa, joka on esitetty alla olevassa taulukossa.
| Kvadrantti | Pisteen yleinen muoto tässä kvadrantissa | Esimerkki | Kuvaus |
|---|---|---|---|
| I | (+,+) | (5,4) | Aloitetaan origosta x-akselia pitkin positiiviseen suuntaan (oikealle) ja y-akselia pitkin positiiviseen suuntaan (ylös). |
| II | (-,+) | (-5,4) | Aloitetaan origosta x-akselia pitkin negatiiviseen suuntaan (vasemmalle) ja y-akselia pitkin positiiviseen suuntaan (ylös). |
| III | (-,-) | (-5,-4) | Aloitetaan origosta x-akselia pitkin negatiiviseen suuntaan (vasemmalle) ja y-akselia pitkin negatiiviseen suuntaan (alas). |
| IV | (+,-) | (5,-4) | Aloitetaan origosta x-akselia pitkin positiiviseen suuntaan (oikealle) ja y-akselia pitkin negatiiviseen suuntaan (alas). |
Kun tunnet koordinaattitason kvadrantit, voit määrittää järjestetyn parin kvadrantin ilman, että edes kuvaat sitä graafisesti, katsomalla yllä olevaa taulukkoa. Tässä on toinen tapa ajatella asiaa.
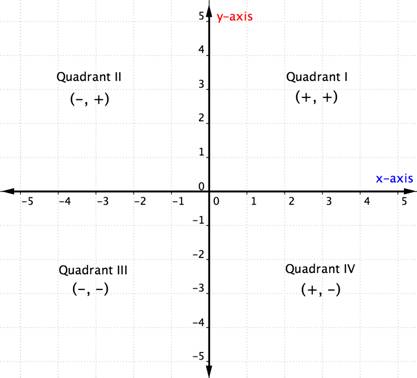
Alla olevassa esimerkissä kerrotaan yksityiskohtaisesti, miten pisteen kvadranttipaikka määritetään vain ajattelemalla sen koordinaattien merkkejä. Kvadrantin sijainnin miettiminen ennen pisteen piirtämistä voi auttaa sinua välttämään virheen. Se on myös hyödyllistä tietoa tarkistettaessa, että olet piirtänyt pisteen oikein.
Esimerkki
Missä kvadrantissa piste (-7,10) sijaitsee?
Esimerkki
Missä kvadrantissa piste (-10,-5) sijaitsee?
Mitä tapahtuu, jos järjestetyn parin x- tai y-koordinaatti on nolla? Alla olevassa esimerkissä on järjestetyn parin (0,4) kuvaaja.
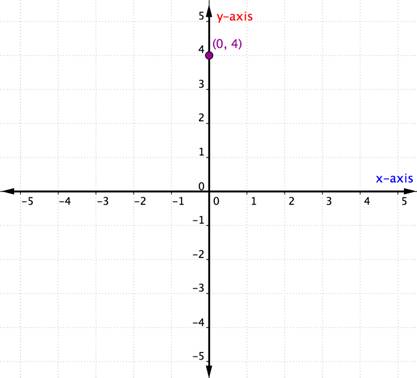
Pisteen, joka sijaitsee yhdellä akseleista, ei katsota olevan kvadrantissa. Se on yksinkertaisesti yhdellä akseleista. Aina kun x-koordinaatti on 0, piste sijaitsee y-akselilla. Vastaavasti mikä tahansa piste, jonka y-koordinaatti on 0, sijaitsee x-akselilla.
Tunnista kvadrantit ja käytä niitä pisteiden piirtämiseen
Yhteenveto
Koordinaattitaso on järjestelmä pisteiden ja suorien kuvaamiseen ja kuvaamiseen. Koordinaattitaso koostuu vaaka-akselista (x-) ja pystyakselista (y-). Näiden viivojen leikkauspiste muodostaa origon, joka on piste (0,0). Koordinaattitaso on jaettu neljään kvadranttiin. Yhdessä nämä koordinaatiston ominaisuudet mahdollistavat pisteiden, suorien ja muiden algebrallisten käsitteiden graafisen esittämisen ja viestinnän.





